【洛谷P3216】【BZOJ2326】数学作业【矩阵乘法】

题目大意：

题目链接：
洛谷：https://www.luogu.org/problemnew/show/P3216
Bzoj：https://www.lydsy.com/JudgeOnline/problem.php?id=2326
求$\overline{123...n}\ \%\ m$

---

思路：

这种矩阵乘法的题目一看$n\leq 10^{18}$的数据范围就明显地提示了算法。。。
思路还是很简单的。对于任意的$f[i]$表示$\overline{123...i}\ \%\ m$，$f[i+1]$显然等于
$(f[i]\times cnt+i+1)\ \%\ m$
其中$cnt$表示$i+1$的位数。
显然，对于任意不同位数的$i$，需要分开来矩乘。

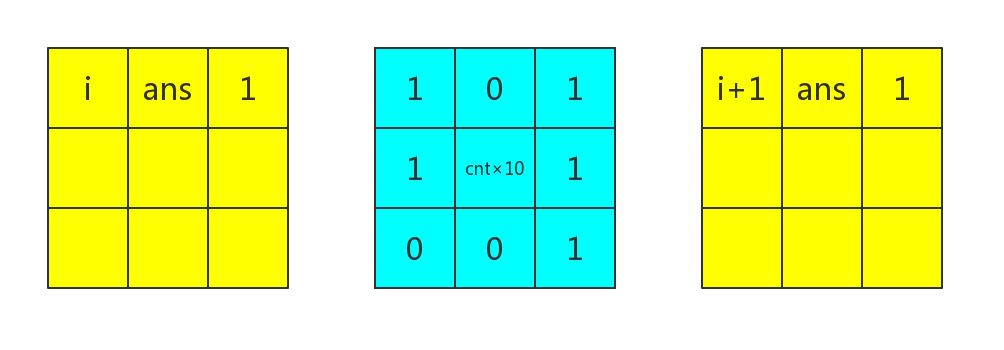
注意$long\ long\times long\ long$可能会爆炸。
时间复杂度$O(log\ n)$

---

代码：

#include <cstdio>
#include <cstring>
using namespace std;
typedef long long ll;

ll n,k,MOD,f[4],a[4][4];

void mul(ll f[4],ll a[4][4])
{
	ll c[4]={0,0,0,0};
	for (int i=1;i<=3;i++)
		for (int j=1;j<=3;j++)
			c[i]=(c[i]+f[j]*a[i][j])%MOD;
	memcpy(f,c,sizeof(c)); 
}

void mulself(ll a[4][4])
{
	ll c[4][4];
	memset(c,0,sizeof(c));
	for (int i=1;i<=3;i++)
		for (int j=1;j<=3;j++)
			for (int k=1;k<=3;k++)
				c[i][j]=(c[i][j]+a[i][k]*a[k][j])%MOD;
	memcpy(a,c,sizeof(c)); 
}

int  main()
{
	scanf("%lld%lld",&n,&MOD);
	f[1]=0,f[2]=0,f[3]=1;
	for (ll m=1;m<=n;m*=10)
	{
		if (m>n/10) k=n-m+1;  //这个位数要矩乘的次数
			else k=m*9;
		a[1][1]=1; a[1][2]=0; a[1][3]=1;
		a[2][1]=1; a[2][2]=m*10%MOD; a[2][3]=1;
		a[3][1]=0; a[3][2]=0; a[3][3]=1;  //重置a数组
		while (k)
		{
			if (k&1) mul(f,a);
			mulself(a);
			k>>=1;
		}	
	}
	printf("%lld",f[2]);
	return 0;
}