【JZOJ4787】数格子【矩阵乘法】

题目大意：

题目链接：https://jzoj.net/senior/#main/show/4787
求用$1\times 2$的骨牌铺满$4\times n$的方格的方案数。

---

思路：

这种类型的题目很显然是公式或者规律的。况且$n\leq 10^9$这种$O(n)$都不可以过的还能有什么做法XD
惯例：打表找规律。

$n$	1	2	3	4	5	6	7	8	9	10
$ans$	1	5	11	36	95	281	781	2245	6336	18061

肉眼看了$5min$还是什么都没看出来。
这是个好网站
往下翻，就可以看到
$a(n)=a(n-1)+5*a(n-2)+a(n-3)-a(n-4)$

所以利用这个公式就可以拿到$60pts$的高分了。
这个显然是可以用矩阵乘法搞的呀。

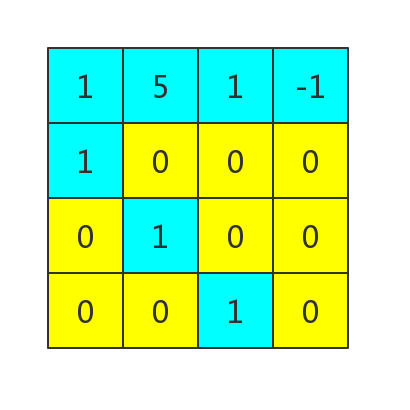
这样复杂度就是$\log$级别的了。

---

代码：

#include <cstdio>
#include <cstring>
#include <iostream>
using namespace std;
typedef long long ll;

const ll A[5][5]=
{
	{0,0,0,0,0},
	{0,1,5,1,-1},
	{0,1,0,0,0},
	{0,0,1,0,0},
	{0,0,0,1,0}
};

int n,MOD;
ll f[5],a[5][5];

void mul(ll f[5],ll a[5][5])
{
	ll c[5]={0,0,0,0,0};
	for (int i=1;i<=4;i++)
		for (int j=1;j<=4;j++)
			c[i]=(c[i]+a[i][j]*f[j])%MOD;
	memcpy(f,c,sizeof(c));
}

void mulself(ll a[5][5])
{
	ll c[5][5];
	memset(c,0,sizeof(c));
	for (int i=1;i<=4;i++)
		for (int j=1;j<=4;j++)
			for (int k=1;k<=4;k++)
				c[i][j]=(c[i][j]+a[i][k]*a[k][j])%MOD;
	memcpy(a,c,sizeof(c));
}

/*
1,5,11,36,95,281,781,2245,6336,18061
a(n)=a(n-1)+5*a(n-2)+a(n-3)-a(n-4)
*/

int main()
{
	while (scanf("%d%d",&n,&MOD)==2 && n && MOD)
	{
		if (n==1) {printf("1\n"); continue;}
		if (n==2) {printf("5\n"); continue;}
		if (n==3) {printf("11\n"); continue;}
		if (n==4) {printf("36\n"); continue;}
		memcpy(a,A,sizeof(A));
		f[1]=36,f[2]=11,f[3]=5,f[4]=1;
		n-=4;
		while (n)
		{
 			if (n&1) mul(f,a);
			mulself(a);
			n>>=1;
		}
		cout<<(f[1]%MOD+MOD)%MOD<<endl;
	}
	return 0;
}