【洛谷P4997】不围棋【并查集】【模拟】
题目大意:
题目链接:https://www.luogu.org/problemnew/show/P4997
「不围棋」是一种非常有趣的棋类游戏。
大家都知道,围棋的「气」是指一个棋子所在的联通块相邻的空格。两粒棋如果在棋盘上线段的两端就认为是相邻的,也就是在同一个连通块里。比如在图中,白子为四个独立的连通块,黑子构成一个连通块,绿色点是黑子连通块唯一的「气」:
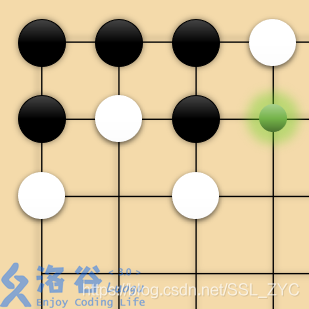
「提子」是指将没有「气」的棋子提出棋盘,在上图中,如果白方走绿点,那么就可以将黑子全部提走。
在围棋中,我们想尽量多地占领地盘、提走对方棋子。然而,不围棋恰恰相反——不围棋是一种非常和平的游戏,双方的走子不能产生任何提子,也就是说,任何一次走子不能让棋盘上任何一个棋子所在的连通块没有气。比如,白方在上图中不能走绿点。
在你的某一步棋后,对方无棋可走,那么你就赢了。
小 F 对不围棋特别感兴趣,不过他经常输,所以他想做出一个 AI 来替他完成这局游戏。
不过造 AI 实在是太困难啦,小 F 千辛万苦写出来的 AI 被同学们的 AI 锤爆啦!
现在,他想请你帮他实现一个 AI 中一部分的功能——随机模拟,因为他相信你写的程序非常优秀,一定能优化他的 AI。
给你一个 的棋盘,上面或许已经有一些棋子了,但此时局面一定是合法的,即不存在没有气的连通块;此时轮到黑棋下棋,因此棋盘上黑白棋子的数量一定是相等的。
你的任务是,依次为黑棋和白棋随意指定一个可行的走子位置,直到某一步游戏无法进行,决出胜负为止。
在正式的不围棋比赛还存在一些禁手规则。不过由于小 F 玩的是一种棋盘大小可变的新型不围棋,我们只用考虑上面提到的气的规则就好。
思路:
好久好久没有敲这种基本不用算法优化的大模拟题了 虽然这道题用了并查集 。
这道题2018年11月就决定敲。打来打去搞了好几次。这下总算是搞定这道题了。
评测记录
这道题有SPJ,所以就顺序枚举黑棋白棋落子点。
先说一下大体思路吧
显然直接模拟是的。所以考虑用并查集记录连通块和气,然后再记录下上一次黑棋白棋放置的位置,直接从那个位置往下枚举即可。
先处理好初始的连通块和气。
每次判断这个落子点是否可行。如果可以,那么就把棋子落在这里,并维护上下左右棋子的气,维护联通集合。
为了简便起见,我们修改一下气的定义。一个连通块的气为该连通块,其中表示棋子的上下左右有几个空格子。
这样定义的话,下图黑棋的气就是5气,而不是2气。
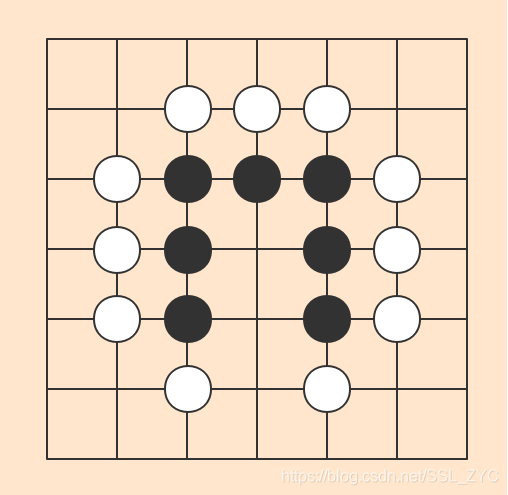
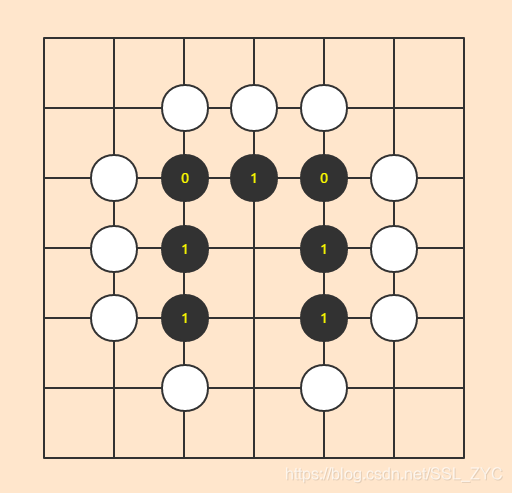
这样的好处是:如果我们用白棋填上最中间的位置,黑棋的气就只要减去3就可以了。否则的话还只能判断这个白棋所连接的黑棋是否是在同一个连通块内,会比较麻烦。
1.如何判断能否落子
一个点不可以落子,只有满足以下任意条件才行:
- 落子后,周围另一方的棋子的气变成0
- 落子后,这个子及所在连通块的气为0
周围另一方棋子的气是比较好判断的。只要把周围所有的对方棋子所在连通块气减1,然后判断这些连通块内是否有块没气了。只要有1个块没气,就是不可以落子的。
if (map[i-1][j]==oth) sum[find(C(i-1,j))]--;
if (map[i+1][j]==oth) sum[find(C(i+1,j))]--;
if (map[i][j-1]==oth) sum[find(C(i,j-1))]--;
if (map[i][j+1]==oth) sum[find(C(i,j+1))]--;
//。。。。。。
//判断这个子及所在连通块的气是否为0
bool ok=0;
if (sum[find(C(i-1,j))] && sum[find(C(i+1,j))] && sum[find(C(i,j-1))] && sum[find(C(i,j+1))])
ok=1;
if (map[i-1][j]==oth) sum[find(C(i-1,j))]++;
if (map[i+1][j]==oth) sum[find(C(i+1,j))]++;
if (map[i][j-1]==oth) sum[find(C(i,j-1))]++;
if (map[i][j+1]==oth) sum[find(C(i,j+1))]++;
判断这个子及所在连通块的气是否为0的话,先假设这个点的气为4,如果上下左右有棋子和该棋子的颜色相同,那么就加上这个连通块的气,但是同时也要减去2。因为在没有落子之前,该连通块有1气是在这个点上的,但是现在这个点落子了,这个气就没有了。并且我们一开始假设的气为4,但是现在并不是上下左右都是空的,还要减去1。
然后,如果这个点的上下左右是边界或者对方棋子,气也要减少。
int s=4;
if (map[i-1][j]==ch)
{
s-=2;
if (!vis[find(C(i-1,j))]) //注意,每个连通块的气只能加一次,所以要判断这个连通块是否加过
{
vis[find(C(i-1,j))]=1;
s+=sum[find(C(i-1,j))];
}
}
if (map[i+1][j]==ch)
{
s-=2;
if (!vis[find(C(i+1,j))])
{
vis[find(C(i+1,j))]=1;
s+=sum[find(C(i+1,j))];
}
}
if (map[i][j-1]==ch)
{
s-=2;
if (!vis[find(C(i,j-1))])
{
vis[find(C(i,j-1))]=1;
s+=sum[find(C(i,j-1))];
}
}
if (map[i][j+1]==ch)
{
s-=2;
if (!vis[find(C(i,j+1))])
{
vis[find(C(i,j+1))]=1;
s+=sum[find(C(i,j+1))];
}
}
vis[find(C(i-1,j))]=vis[find(C(i+1,j))]=vis[find(C(i,j-1))]=vis[find(C(i,j+1))]=0; //还原
if (map[i-1][j]==oth||i==1) s--;
if (map[i+1][j]==oth||i==n) s--;
if (map[i][j-1]==oth||j==1) s--;
if (map[i][j+1]==oth||j==n) s--; //判断边界和对方棋子
bool ok=0;
if (s) ok=1;
这样,我们的函数就写好了。
2.如何合并连通块
这个应该相对简单吧。
需要解决的问题有3个。
- 新连通块的气
- 如何合并连通块
- 对手连通块的气
其实不用处理新连通块的气。因为我们在函数里已经判断了落子后这个连通块的气是否大于0,而用到的变量就是这个连通块的气。如果这个位置可以落子,那么直接把气赋值给就可以了。
合并连通块其实就是最基本的并查集操作,如果上下左右是我方棋子,那么就将这个连通块和合并。
处理对手的气也是非常简单的。由于我们把气的定义更改了,所以就不用判断“上和下的两个连通块是否是同一个连通块”之类的问题了。直接取上下左右的连通块的祖先,把它的气减1就可以了。
map[X][Y]=push;
if (map[X-1][Y]==map[X][Y]) father[find(C(X-1,Y))]=find(C(X,Y));
if (map[X+1][Y]==map[X][Y]) father[find(C(X+1,Y))]=find(C(X,Y));
if (map[X][Y-1]==map[X][Y]) father[find(C(X,Y-1))]=find(C(X,Y));
if (map[X][Y+1]==map[X][Y]) father[find(C(X,Y+1))]=find(C(X,Y));
char oth=(push=='X'?'O':'X');
if (map[X-1][Y]==oth) sum[find(C(X-1,Y))]--;
if (map[X+1][Y]==oth) sum[find(C(X+1,Y))]--;
if (map[X][Y-1]==oth) sum[find(C(X,Y-1))]--;
if (map[X][Y+1]==oth) sum[find(C(X,Y+1))]--;
printf("%d %d\n",X,Y);
if (push=='X') pushX=C(X,Y)+1;
else pushO=C(X,Y)+1;
push=(push=='X'?'O':'X');
然后这道大模拟就这样切了。
代码:
#include <cstdio>
#include <cstring>
using namespace std;
const int N=610;
int n,X,Y,pushX,pushO,father[N*N],sum[N*N];
char map[N][N],push;
bool vis[N*N];
int find(int x)
{
return x==father[x]?x:father[x]=find(father[x]);
}
int C(int x,int y)
{
if (x>n||y>n||x<1||y<1) return 0;
return (x-1)*n+y;
}
bool check_push(char ch)
{
char oth=(ch=='X'?'O':'X');
for (int k=(ch=='X'?pushX:pushO);k<=n*n;k++)
{
int i=(k-1)/n+1;
int j=(k-1)%n+1;
if (map[i][j]=='.')
{
if (map[i-1][j]==oth) sum[find(C(i-1,j))]--;
if (map[i+1][j]==oth) sum[find(C(i+1,j))]--;
if (map[i][j-1]==oth) sum[find(C(i,j-1))]--;
if (map[i][j+1]==oth) sum[find(C(i,j+1))]--;
int s=4;
if (map[i-1][j]==ch)
{
s-=2;
if (!vis[find(C(i-1,j))])
{
vis[find(C(i-1,j))]=1;
s+=sum[find(C(i-1,j))];
}
}
if (map[i+1][j]==ch)
{
s-=2;
if (!vis[find(C(i+1,j))])
{
vis[find(C(i+1,j))]=1;
s+=sum[find(C(i+1,j))];
}
}
if (map[i][j-1]==ch)
{
s-=2;
if (!vis[find(C(i,j-1))])
{
vis[find(C(i,j-1))]=1;
s+=sum[find(C(i,j-1))];
}
}
if (map[i][j+1]==ch)
{
s-=2;
if (!vis[find(C(i,j+1))])
{
vis[find(C(i,j+1))]=1;
s+=sum[find(C(i,j+1))];
}
}
vis[find(C(i-1,j))]=vis[find(C(i+1,j))]=vis[find(C(i,j-1))]=vis[find(C(i,j+1))]=0;
if (map[i-1][j]==oth||i==1) s--;
if (map[i+1][j]==oth||i==n) s--;
if (map[i][j-1]==oth||j==1) s--;
if (map[i][j+1]==oth||j==n) s--;
bool ok=0;
if (s && sum[find(C(i-1,j))] && sum[find(C(i+1,j))] && sum[find(C(i,j-1))] && sum[find(C(i,j+1))])
ok=1;
if (map[i-1][j]==oth) sum[find(C(i-1,j))]++;
if (map[i+1][j]==oth) sum[find(C(i+1,j))]++;
if (map[i][j-1]==oth) sum[find(C(i,j-1))]++;
if (map[i][j+1]==oth) sum[find(C(i,j+1))]++;
if (ok)
{
sum[C(i,j)]=s;
X=i,Y=j;
return 1;
}
}
}
return 0;
}
int main()
{
memset(sum,0x3f3f3f3f,sizeof(sum));
scanf("%d",&n);
for (int i=1;i<=n;i++)
for (int j=1;j<=n;j++)
{
map[i][j]=getchar();
while (map[i][j]!='X'&&map[i][j]!='O'&&map[i][j]!='.')
map[i][j]=getchar();
father[C(i,j)]=C(i,j);
}
for (int i=1;i<=n;i++)
for (int j=1;j<=n;j++)
{
sum[C(i,j)]=0;
if (map[i-1][j]==map[i][j]&&map[i][j]!='.')
father[find(C(i,j))]=find(C(i-1,j));
if (map[i][j-1]==map[i][j]&&map[i][j]!='.')
father[find(C(i,j))]=find(C(i,j-1));
if (map[i-1][j]=='.') sum[find(C(i,j))]++;
if (map[i+1][j]=='.') sum[find(C(i,j))]++;
if (map[i][j+1]=='.') sum[find(C(i,j))]++;
if (map[i][j-1]=='.') sum[find(C(i,j))]++;
}
push='X';
pushX=pushO=1;
while (check_push(push))
{
map[X][Y]=push;
if (map[X-1][Y]==map[X][Y]) father[find(C(X-1,Y))]=find(C(X,Y));
if (map[X+1][Y]==map[X][Y]) father[find(C(X+1,Y))]=find(C(X,Y));
if (map[X][Y-1]==map[X][Y]) father[find(C(X,Y-1))]=find(C(X,Y));
if (map[X][Y+1]==map[X][Y]) father[find(C(X,Y+1))]=find(C(X,Y));
char oth=(push=='X'?'O':'X');
if (map[X-1][Y]==oth) sum[find(C(X-1,Y))]--;
if (map[X+1][Y]==oth) sum[find(C(X+1,Y))]--;
if (map[X][Y-1]==oth) sum[find(C(X,Y-1))]--;
if (map[X][Y+1]==oth) sum[find(C(X,Y+1))]--;
printf("%d %d\n",X,Y);
if (push=='X') pushX=C(X,Y)+1;
else pushO=C(X,Y)+1;
push=(push=='X'?'O':'X');
}
printf("-1 -1\n");
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号