【洛谷P4838】P哥破解密码【矩阵乘法】

题目大意：

题目链接：https://www.luogu.org/problemnew/show/P4838
求长度为$n$的只包含$AB$的字符串且没有任意三个$A$相连的字符串个数。

---

思路：

因为有不能任意三个$A$相连的限制，所以可以讨论长度为$n$的字符串的后缀方案及对$n+1$的影响。
首先，长度为$n$的字符串后缀总数只有3个：

• 后缀为$ba$。这样显然只能由倒数第二个位置为$b$的字符串得来。
• 后缀为$aa$。这样显然只能由倒数第二个位置为$a$的字符串得来。
• 后缀为$b$。这样显然去掉$b$后的后缀为$ba,aa$还是$b$都是无所谓的。

设$f[n][s]$表示长度为$n$的后缀为$s$的字符串的个数，那么有
$f[n][ba]=f[n-1][b]$
$f[n][aa]=f[n-1][a]$
$f[n][b]=f[n-1][ba]+f[n-1][aa]+f[n-1][b]$
所以我们可以构造出如下矩阵：

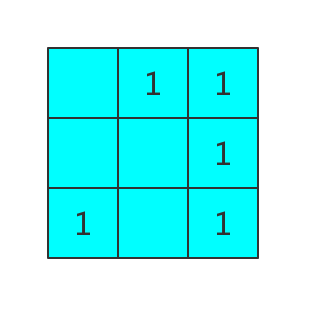
然后每次询问都跑一边矩阵乘法就行了。

---

代码：

#include <cstdio>
#include <cstring>
using namespace std;
typedef long long ll;

const ll MOD=19260817;
int n,m;

struct matrix
{
	ll a[4][4];
}f,A,a;
 
matrix operator *(matrix a,matrix b)
{
	matrix c;
	memset(c.a,0,sizeof(c.a));
	for(int i=1;i<=3;i++)
		for(int j=1;j<=3;j++)
	  		for(int k=1;k<=3;k++)
	      		c.a[i][j]=(c.a[i][j]+a.a[i][k]*b.a[k][j])%MOD;
	return c;
}

void power(int M)
{
	for (;M;M>>=1,a=a*a)
		if (M&1) f=f*a;
}

int main()
{
	A.a[3][1]=A.a[1][2]=A.a[1][3]=A.a[2][3]=A.a[3][3]=1;
	scanf("%d",&m);
	while (m--)
	{
		memcpy(a.a,A.a,sizeof(A.a));
		memset(f.a,0,sizeof(f.a));
		f.a[1][1]=f.a[1][3]=1;
		scanf("%d",&n);
		power(n-1);
		printf("%lld\n",(f.a[1][1]+f.a[1][2]+f.a[1][3])%MOD);
	}
	return 0;
}