【洛谷P3965】循环格【费用流】

题目大意：

题目链接：https://www.luogu.org/problemnew/show/P3965
一个完美的循环格是这样定义的:对于任意一个起始位置,你都可以沿着箭头最终回到起始位置。如果一个循环格不满足完美,你可以随意修改任意一个元素的箭头直到完美。例如下图,左边不是一个完美的循环格,因为只有从$(1,1),(1,2),(2,0),(2,3)$出发才会回到起始位置。通过修改其中两个箭头,可以得到右图,一个完美的循环格。

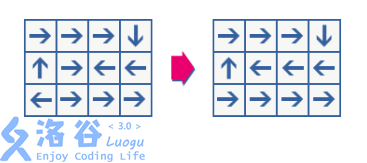
给定一个循环格,你需要计算最少需要修改多少个元素使其完美。

---

思路：

一眼题啊，最多蓝题。题解和标签都没看就过了。
先证明完美循环格所有的点入度为1。

• 点的入度必然为自然数。。。
• 点的入度必然不等于0。若某点的入度为0则没有任何点可以到达这个点。显然这个图不是完美的。
• 点的入度必然小于2。显然每个点的出度为1，共$n\times m$个点。又因为有向图的入度之和等于出度之和，所以这张图的入度为$n\times m$。若有一个点的入度大于等于2，则必有至少一个点的入度为0，矛盾。
• 所以完美循环格所有的点入度为1

所以我们可以大胆猜想，所有点入度均为1的图就是完美的。
所以可以把所有点拆成入点和出点，出点向四周的入点连边，若和原来的方向一致则费用为0，否则费用为1。
源点连向所有出点，所有入点连向汇点。图中所有边流量为1。显然这个图的最大流是$n\times m$，所以可以保证最终的费用答案是可以满足条件的。

---

代码：

#include <queue>
#include <cstdio>
#include <cstring>
using namespace std;

const int N=1010,M=50010,Inf=1e9;
const char way[]={'\000','U','D','L','R'};
int n,m,tot=1,S,T,cost,head[N],dis[N],pre[N];
bool vis[N];
char ch;

struct edge
{
	int next,to,from,flow,cost;
}e[M];

int C(int x,int y)
{
	return (x-1)*m+y;
}

void add(int from,int to,int flow,int cost)
{
	e[++tot].to=to;
	e[tot].from=from;
	e[tot].flow=flow;
	e[tot].cost=cost;
	e[tot].next=head[from];
	head[from]=tot;
}

bool spfa()
{
	memset(dis,0x3f3f3f3f,sizeof(dis));
	memset(vis,0,sizeof(vis));
	queue<int> q;
	q.push(S);
	dis[S]=0; vis[S]=1;
	while (q.size())
	{
		int u=q.front(),v;
		q.pop();
		vis[u]=0;
		for (int i=head[u];~i;i=e[i].next)
		{
			v=e[i].to;
			if (e[i].flow&&dis[v]>dis[u]+e[i].cost)
			{
				dis[v]=dis[u]+e[i].cost;
				pre[v]=i;
				if (!vis[v])
				{
					vis[v]=1;
					q.push(v);
				}
			}
		}
	}
	return dis[T]<Inf;
}

void addflow()
{
	int minflow=Inf;
	for (int x=T;x!=S;x=e[pre[x]].from)
		minflow=min(minflow,e[pre[x]].flow);
	for (int x=T;x!=S;x=e[pre[x]].from)
	{
		e[pre[x]].flow-=minflow;
		e[pre[x]^1].flow+=minflow;
	}
	cost+=dis[T]*minflow;
}

int MCMF()
{
	while (spfa())
		addflow();
	return cost;
}

int main()
{
	memset(head,-1,sizeof(head));
	scanf("%d%d",&n,&m);
	S=N-1; T=N-2;
	for (int i=1;i<=n;i++)
		for (int j=1;j<=m;j++)
		{
			while (ch=getchar()) if (ch>='A' && ch<='Z') break;
			add(S,C(i,j),1,0); add(C(i,j),S,0,0);
			add(C(i,j)+n*m,T,1,0); add(T,C(i,j)+n*m,0,0);
			for (int k=1;k<=4;k++)
			{
				int x=i,y=j;
				if (way[k]=='U') x--;
				if (way[k]=='D') x++;
				if (way[k]=='L') y--;
				if (way[k]=='R') y++;
				x=(x+n-1)%n+1;
				y=(y+m-1)%m+1;
				if (ch==way[k]) add(C(i,j),C(x,y)+n*m,1,0),add(C(x,y)+n*m,C(i,j),0,0);
					else add(C(i,j),C(x,y)+n*m,1,1),add(C(x,y)+n*m,C(i,j),0,-1);
			}
		}
	MCMF();
	printf("%d\n",cost);
	return 0;
}