【JZOJ3318】【LOJ2685】Brunhilda 的生日【数论，数学】

题目大意：

题目链接：https://loj.ac/problem/2685

---

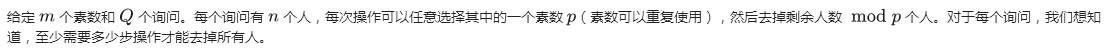
思路：

显然离线。
设$f[x]$表示人数为$x$时的答案。可以证明$f[x]$为单调递增的。
对于一个答案相同的区间$[x,y]$，设$x$的在给定集合里的最大质因子为$p$，则显然$x\sim x+p-1$的答案与$x$相同。因为$gcd(x+p,x)=p$，所以$ans[x+p]=ans[x]+1$，然后$ans[x]\leq ans[x+p-1]<ans[x+p]$。
所以预处理出关于每一个$x$的$p$（复杂度$O(maxn\log \log n)$），然后就可以$O(m)$直接回答了。

---

代码：

#include <queue>
#include <cstdio>
#include <string>
using namespace std;

const int N=10000010;
int n,m,x,maxn,p[N],v[N],ask[N],ans[N];
queue<int> q;

int read()
{
	int d=0;
	char ch=getchar();
	while (!isdigit(ch)) ch=getchar();
	while (isdigit(ch))
		d=(d<<3)+(d<<1)+ch-48,ch=getchar();
	return d;
}

int main()
{
	n=read(); m=read();
	for (int i=1;i<=n;i++)
		p[i]=read();
	for (int i=1;i<=m;i++)
	{
		ask[i]=read();
		if (ask[i]>maxn) maxn=ask[i];
	}
	for (int i=1;i<=n;i++)
		for (int j=p[i];j<=maxn;j+=p[i])
			v[j]=p[i];
	v[0]=p[n];
	q.push(0);
	for (int i=1;q.size()&&i<=maxn;)
	{
		x=q.front();
		q.pop();
		if (v[x])
			for (;i<x+v[x] && i<=maxn;i++)
			{
				ans[i]=ans[x]+1;
				q.push(i);
			}
	}
	for (int i=1;i<=m;i++)
		if (ans[ask[i]] || !ask[i]) printf("%d\n",ans[ask[i]]);
			else printf("oo\n");
	return 0;
}