【JZOJ3833】平坦的折线【dp】【二分】

题目大意：

题目链接：https://jzoj.net/senior/#main/show/3833
现在我们在一张纸上有一个笛卡尔坐标系。我们考虑在这张纸上用铅笔从左到右画的折线。我们要求任何两个点之间连接的直线段与x轴的夹角在-45~45之间，一条满足以上条件的折线称之为平坦的折线。假定给出了n个不同的整点（坐标为整数的点），最少用几条平坦的折线可以覆盖所有的点？
例子：

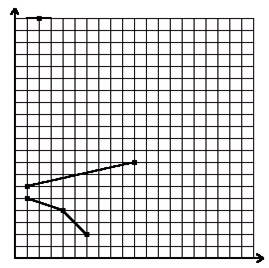
图中有6个整点：(1,6), (10,8), (1,5), (2,20), (4,4), (6,2)，要覆盖它们至少要3条平坦的折线。
任务：
写一个程序：
从文件lam.in中读入点的个数以及它们的坐标。
计算最少需要的折线个数。
将结果写入文件lam.out。

---

思路：

原来的坐标系内的任意一个点可以对与其连线的斜率在$-1\sim 1$之间，如果我们把这个坐标系顺时针旋转$45$°，那么对于新坐标系内的任意一点，它所能贡献的点就位于它的右上方。
那么如何在新坐标系内求出这些点呢？
新坐标系的$y$轴其实就是原坐标系的直线$y=x$。那么如果一个点经过原坐标系的$y=x+k$，那么它在新坐标系的横坐标就是$k$。
同理，新坐标系的$x$轴就是原坐标系的$y=-x$，若一个点过$y=-x+k$，那么这个点在旧坐标系的纵坐标就是$k$。
所以对于一个点$(x,y)$，它的新坐标就是$(y-x,x+y)$。
然后由于只能从左向右选，所以将每一个新点按横坐标排序。
那么接下来就是覆盖$y$的问题了。既然已经满足$x$单调，我们就是要求多少个不降序列可以将每一个点的$y$覆盖掉。
这就是经典的导弹拦截的问题了。只不过是将不升改成了不降。
时间复杂度$O(n\log n)$

---

代码：

#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;

const int N=30010;
int n,x,y,l,r,mid,ans,f[N];

struct node
{
	int x,y;
}a[N];

bool cmp(node x,node y)
{
	if (x.x>y.x) return 1;
	if (x.x<y.x) return 0;
	return x.y<y.y;
}

int main()
{
	freopen("lam.in","r",stdin);
	freopen("lam.out","w",stdout);
	scanf("%d",&n);
	for (int i=1;i<=n;i++)
	{
		scanf("%d%d",&x,&y);
		a[i].x=y-x; a[i].y=x+y;
	}
	sort(a+1,a+1+n,cmp);
	f[0]=2147483647;
	for (int i=1;i<=n;i++)
	{
		if (f[ans]>a[i].y) f[++ans]=a[i].y;
		else
		{
			l=1; r=ans;
			while (l<=r)
			{
				mid=(l+r)>>1;
				if (f[mid]>a[i].y) l=mid+1;
					else r=mid-1;
			}
			f[l]=a[i].y;
		}
	}
	printf("%d\n",ans);
	return 0;
}