高等数学十一：方向导数、梯度

一、向量：

 

 

 

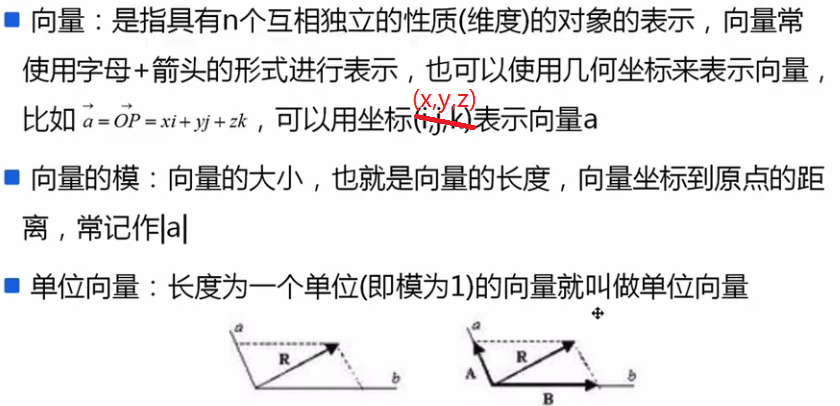
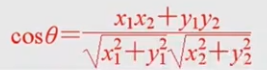
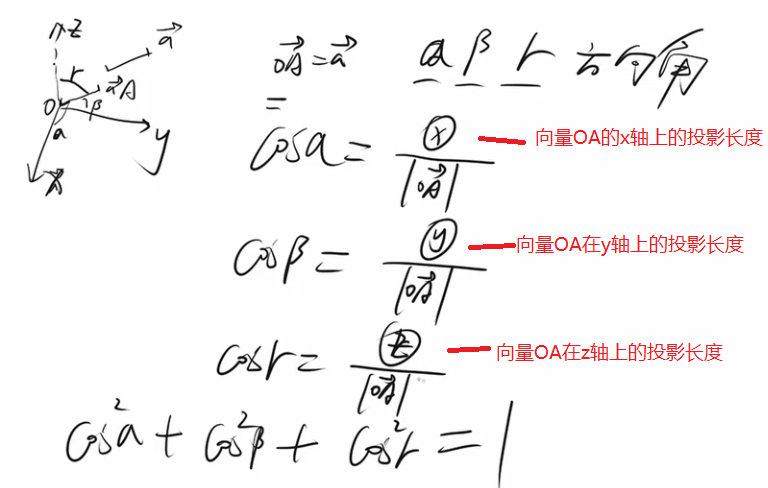
方向角的余弦值：

 

 二、方向导数

 方向导数的定理：

以上的方向导数的定理，对于二元函数的方向导数，肯定也是适用的。如下：

 

cos a  就是在x方向上的投影长度2，与模长度ρ的比值。

cos β 就是在y方向上的投影长度1，与模长度ρ的比值。

cos  γ 就是在z方向上的投影长度3，与模长度ρ的比值。

模长度，就是向量l的模长度，也是它在各个方向上的平方和的开平方，即

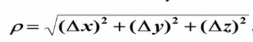
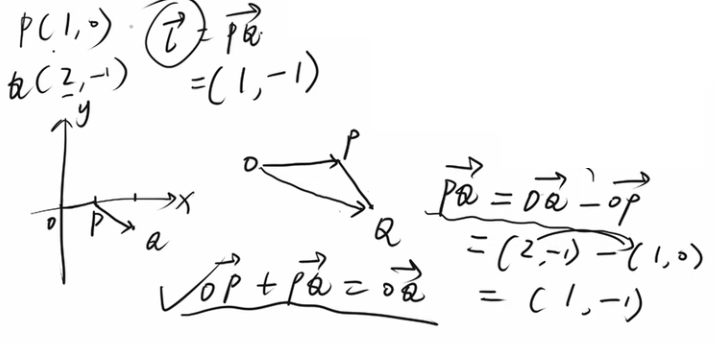
PQ向量的计算：

 

 

三、梯度 

 

梯度的本意是一个向量（矢量），表示某一函数在该点处的方向导数沿着该方向取得最大值，即函数在该点处沿着该方向（此梯度的方向）变化最快，变化率最大（为该梯度的模）。

以上推导公式中的补充：

l^{0的向量，同l的方向量是相等的。}

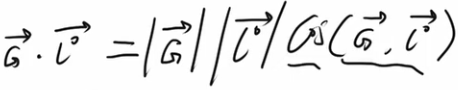
因为

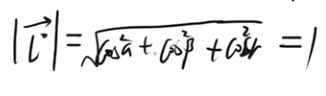
所以推导到此步结果：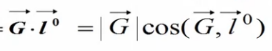

G向量的模：等于各个方向上的偏导数的平方和的开平方：

 

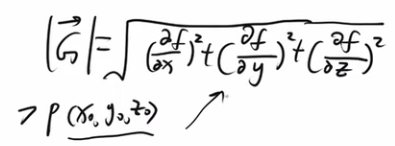
梯度的定义：

 

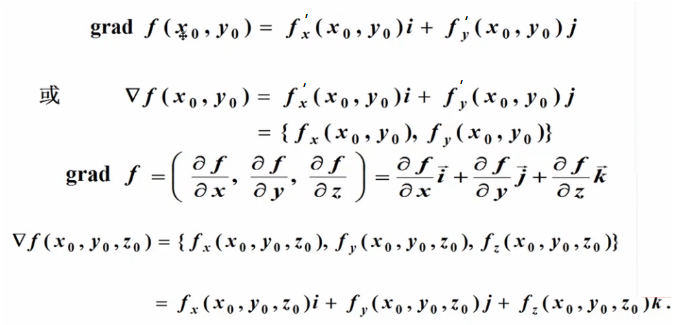
其中i,j,k的向量，表示x,y,z方向上的单位向量。

 

 

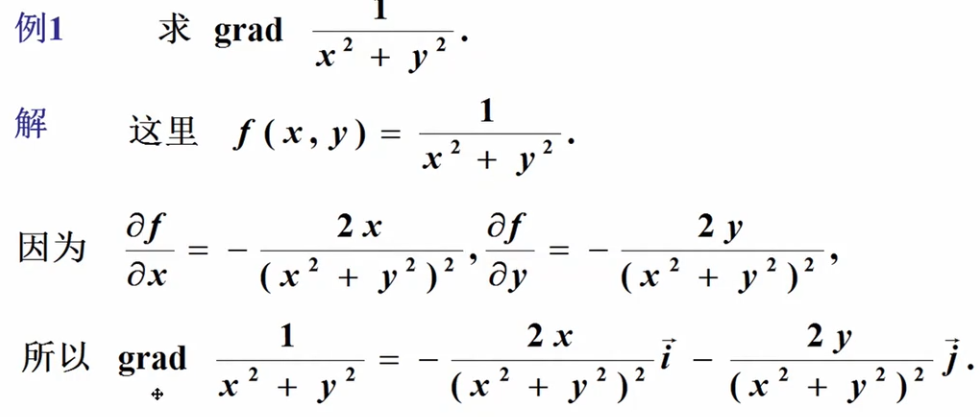
方向导数公式的推导：