『OpenCV3』霍夫变换原理及实现
霍夫变换常用于检测直线特征，经扩展后的霍夫变换也可以检测其他简单的图像结构。
在霍夫变换中我们常用公式
ρ = x*cosθ + y*sinθ
表示直线，其中ρ是圆的半径（也可以理解为原点到直线的距离），θ是直线与水平线所成的角度（0~180°），确定了它们，也就确定一条直线了，和下图略有出入的是实际的原点定在图片左上角。
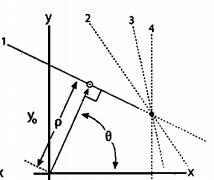
原理是对于输入的二值图像中的像素点（有值的），按照步长（参数三参数四对应rho和theta的步长）分别计算出每个点上的所有可能的直线。记录下每条直线经过的点数（即存在多个点计算出的直线有交集），按照阈值（参数五）筛选符合条件的图像，下面给出基本霍夫变换的由来，原文见：霍夫变换。
基本原理
一条直线可由两个点A=(X1,Y1)和B=(X2,Y2)确定(笛卡尔坐标)
另一方面，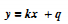
也可以写成关于（k,q）的函数表达式（霍夫空间）：
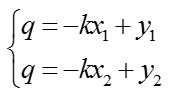
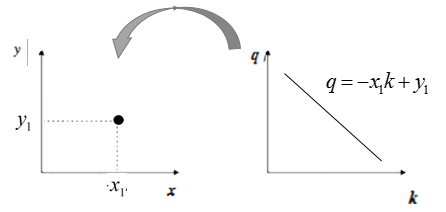
对应的变换可以通过图形直观表示：
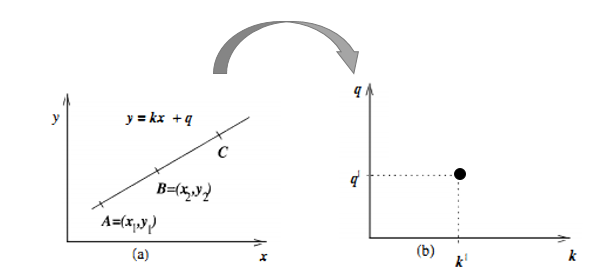
变换后的空间成为霍夫空间。即：笛卡尔坐标系中一条直线，对应霍夫空间的一个点。
反过来同样成立（霍夫空间的一条直线，对应笛卡尔坐标系的一个点）：
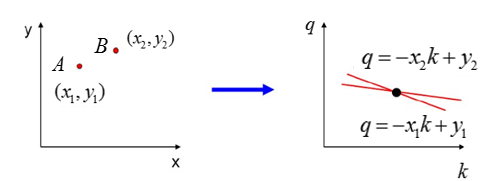
再来看看A、B两个点，对应霍夫空间的情形：
一步步来，再看一下三个点共线的情况：
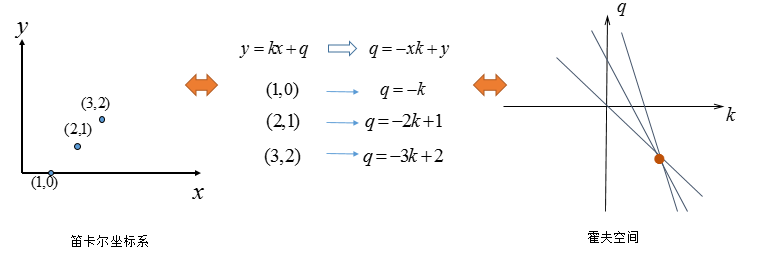
可以看出如果笛卡尔坐标系的点共线，这些点在霍夫空间对应的直线交于一点：这也是必然，共线只有一种取值可能。
如果不止一条直线呢？再看看多个点的情况（有两条直线）：
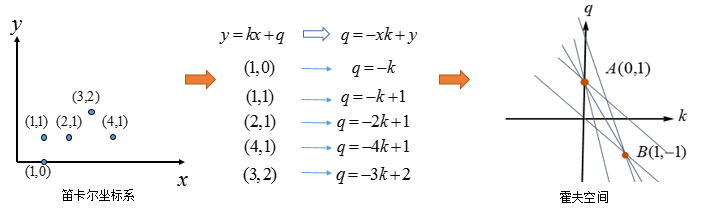
其实（3，2）与（4，1）也可以组成直线，只不过它有两个点确定，而图中A、B两点是由三条直线汇成，这也是霍夫变换的后处理的基本方式：选择由尽可能多直线汇成的点。
看看，霍夫空间：选择由三条交汇直线确定的点（中间图），对应的笛卡尔坐标系的直线（右图）。
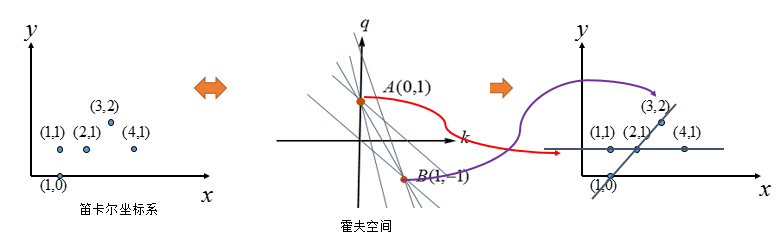
到这里问题似乎解决了，已经完成了霍夫变换的求解，但是如果像下图这种情况呢？
k=∞是不方便表示的，而且q怎么取值呢，这样不是办法。因此考虑将笛卡尔坐标系换为：极坐标表示。
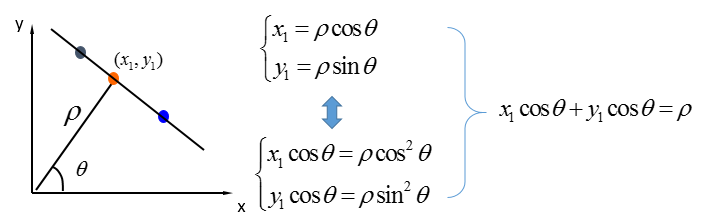
在极坐标系下，其实是一样的：极坐标的点→霍夫空间的直线，只不过霍夫空间不再是[k,q]的参数，而是
的参数，给出对比图：
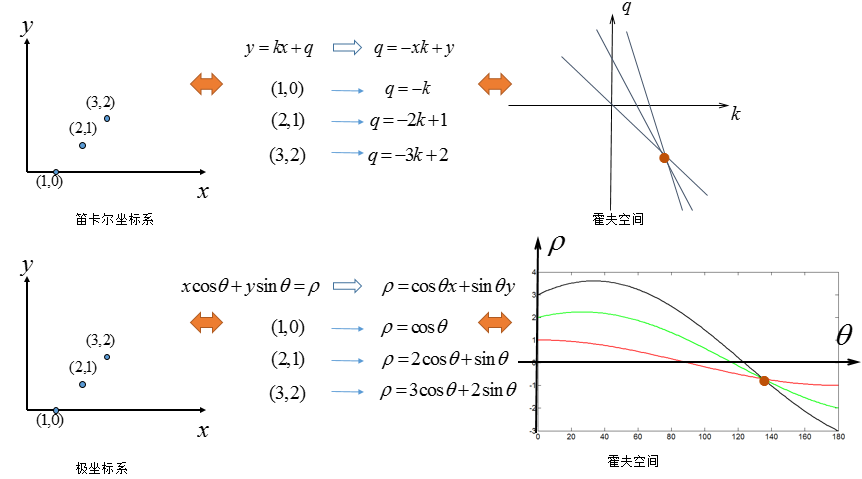
是不是就一目了然了？
给出霍夫变换的算法步骤：
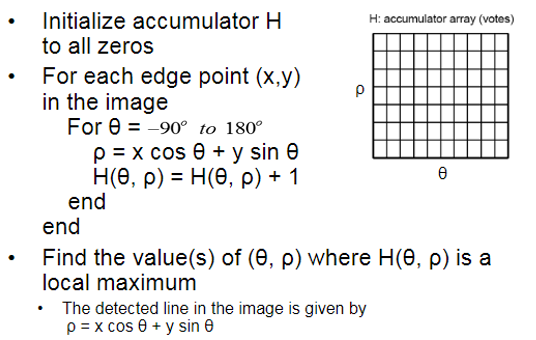
计数过程简易实现如下，我们通过H矩阵记录每一条直线经过的像素点，后续处理实际上已经不算Hough算法的部分了，不予实现了，另外我的H矩阵的行数（即rho的存储部分）设定的非常不严谨，浪费了很多空间，实际实现应考虑优化，确定rho的最小范围，并投影到0~某个正数区间，作为H的行数。
void hough() {
Mat souImg = imread("建筑.png");
imshow("原始图片", souImg);
Mat contour;
Canny(souImg, contour, 50, 200);
imshow("轮廓图片", contour);
int H_row;
if (contour.cols > contour.rows)
H_row = contour.cols;
else
H_row = contour.rows;
Mat H(3*H_row, 180, CV_8S, Scalar(0));
std::cout << H_row << std::endl;
float theta, rho;
for (int i = 0; i < contour.rows; i++) {
for (int j = 0; j < contour.cols; j++) {
if (contour.at<uchar>(i, j) > 0) {
for (theta = 0; theta < 180; ++theta) {
rho = floor(i*cos(theta*CV_PI / 180) + j*sin(theta*CV_PI / 180));
try {
H.at<uchar>(rho + H_row, theta) += 1;
}
catch (...) {
std::cout << i << j << rho << theta << std::endl;
return;
}
}
}
}
}
imshow("H", H);
waitKey(0);
}
1、霍夫变换
霍夫变换接收二值化的输入，即已经进行初步的轮廓检测之后，才进行直线检测；输出一组cv::Vec2f，通常用vector<CV::Vec2f>接收，所以我们通常使用Canny检测之后进行霍夫变换。
输出的两个float数字表示(rho, theta)，使用cv::line绘图，因其参数需要的是线段的两个端点，所以我们不得不进行还原操作。
void hough() {
cv::Mat image = cv::imread("road.png");
cv::Mat midImage;
cv::Canny(image, midImage, 50, 200, 3);
std::vector<cv::Vec2f> lines;
cv::HoughLines(midImage, lines, 1, CV_PI / 180, 150); // 输入的时二值图像，输出vector向量
for (size_t i=0; i < lines.size(); i++) {
float rho = lines[i][0]; //就是圆的半径r
float theta = lines[i][1]; //就是直线的角度
cv::Point pt1, pt2;
double a = cos(theta), b = sin(theta);
double x0 = a*rho, y0 = b*rho;
pt1.x = cvRound(x0 + 1000 * (-b));
pt1.y = cvRound(y0 + 1000 * (a));
pt2.x = cvRound(x0 - 1000 * (-b));
pt2.y = cvRound(y0 - 1000 * (a));
cv::line(image, pt1, pt2, cv::Scalar(55, 100, 195), 1); //Scalar函数用于调节线段颜色，就是你想检测到的线段显示的是什么颜色
cv::imshow("边缘检测后的图", midImage);
cv::imshow("最终效果图", image);
}
}
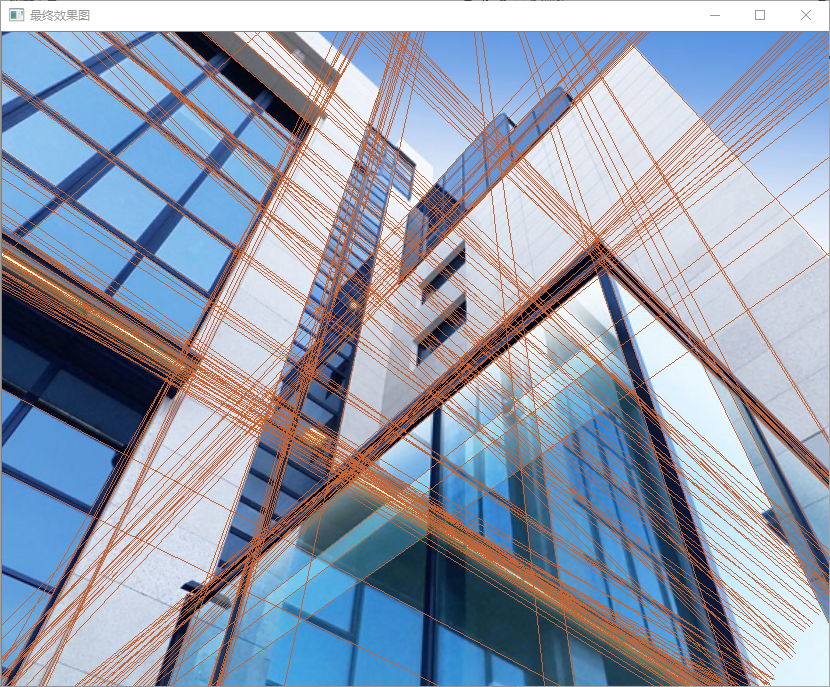
2、概率霍夫变换
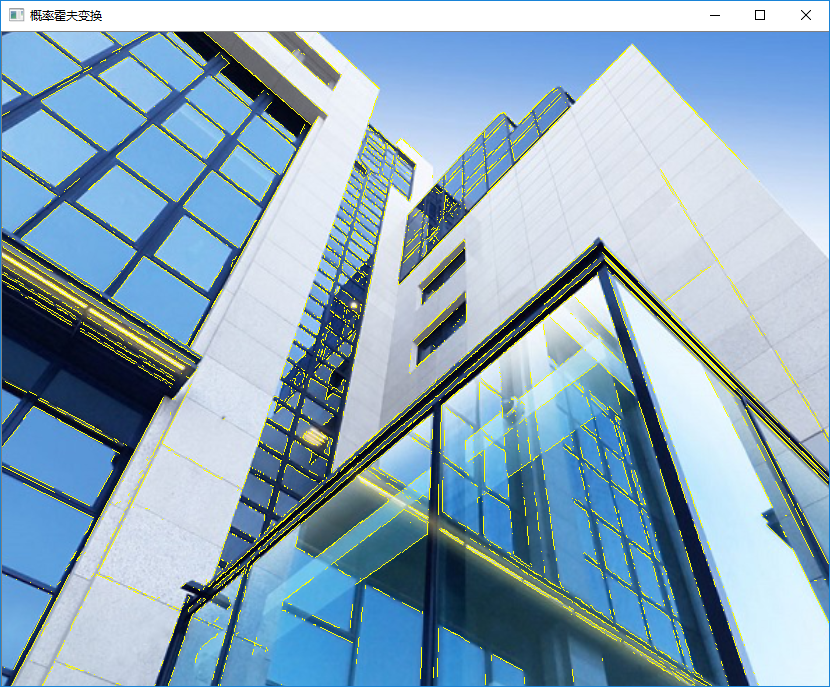
概率霍夫变换输出Vec4i，直接输出了每一条线段的首尾，绘图更加方便。它是霍夫变换的改进版，由于算法的改进（会沿着搜寻到的直线扫描图像），可以进一步检测到线段的长度，除了最小投票数（参数五）外，可以额外限制最小线段长度（参数六）和同一线段最大像素间距（参数七）。
void houghp() {
cv::Mat image = cv::imread("road.png");
cv::Mat midImage;
cv::Canny(image, midImage, 50, 200, 3);
std::vector<cv::Vec4i> lines;
cv::HoughLinesP(midImage, lines, 1, CV_PI / 180, 50); // 输入的时二值图像，输出vector向量
for (int i=0; i < lines.size(); i++) {
cv::Point pt1(lines[i][0], lines[i][1]);
cv::Point pt2(lines[i][2], lines[i][3]);
cv::line(image, pt1, pt2, cv::Scalar(0, 255, 255));
}
cv::imshow("概率霍夫变换", image);
}
