『科学计算』高斯判别分析模型实现

和上一篇一样，本部分的理论建议自行学习cs229或者其他的高斯判别分析模型介绍文章。

1.模型简介

高斯判别分析模型是一种生成模型，而逻辑回归是一种判别模型，生成模型和判别模型的详细了解可参考这篇文章：

http://blog.sciencenet.cn/home.php?mod=space&uid=248173&do=blog&id=227964

首先，高斯判别分析模型对变量x和y有如下假设：

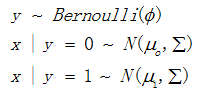
这样，可以给出概率密度函数：

2.评价

该模型的对数似然函数如下：

3.优化

对各个参数进行求导后令等式为0，得到：

　　 Φ是训练样本中结果 y=1 占有的比例。
　　 μ0是 y=0 的样本中特征均值。
　　 μ1是 y=1 的样本中特征均值。
　　 Σ是样本特征方差均值。

代码如下，

import numpy as np
import pandas as pd
from sklearn.datasets import load_iris

# iris = pd.read_csv('http://aima.cs.berkeley.edu/data/iris.csv',
#                    names=['col0','col1','col2','col3','class'])
# dummy = pd.get_dummies(iris['col3'])
# iris = pd.concat([iris, dummy], axis=1)

iris = load_iris()
X = iris.data[:, 0:2]
Y = np.array(pd.get_dummies(iris.target)[0])
# Y = Y[Y[0]==1.]
# print(X[Y==0].mean(axis=0))

def GDA(X, Y):
    theta1 = Y.mean()
    theta0 = 1-theta1
    mu1 = X[Y==1].mean(axis=0)
    mu0 = X[Y==0].mean(axis=0)

    X1 = X[Y==1]
    X0 = X[Y==0]
    A = np.dot(X1.T, X1) - len(Y[Y==1])*np.dot(mu1.reshape(X.shape[1],1), mu1.reshape(X.shape[1],1).T)
    B = np.dot(X0.T, X0) - len(Y[Y==0])*np.dot(mu0.reshape(X.shape[1],1), mu0.reshape(X.shape[1],1).T)
    sigma = (A+B)/len(X)

    return theta1, mu1, mu0, sigma

if __name__=='__main__':
    theta1, mu1, mu0, sigma = GDA(X, Y)
    print(theta1,
          '\r', mu1,
          '\r', mu0,
          '\r', sigma)

我们来检查一下数据，

X.shape
Out[2]:
(150, 2)

Y.shape
Out[3]:
(150,)

由于是二分类问题，实际上我们Y的one_hot只表示属于类别1（1）和其他类别（2）两种标签。

实际上iris是有4个特征的，我们只取了前两个，为什么呢。。。因为我想可视化，高维特征不能可视化233，

简单的把输出

0.333333333333
[ 5.006 3.418]
[ 6.262 2.872]
[[ 0.33055867 0.113388 ]
[ 0.113388 0.12050267]]

导入『科学计算』可视化二元正态分布一节中的可视化函数即可，

import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import axes3d
from matplotlib import cm
import matplotlib as mpl

num = 500
l = np.linspace(0,10,num)
X, Y =np.meshgrid(l, l)
pos = np.concatenate((np.expand_dims(X,axis=2),np.expand_dims(Y,axis=2)),axis=2)

u1 = np.array([5.006, 3.418])
o1 = 3*np.array([[0.33055867, 0.113388],
                 [0.113388, 0.12050267]])
a1 = (pos-u1).dot(np.linalg.inv(o1))
b1 = np.expand_dims(pos-u1,axis=3)
Z1 = np.zeros((num,num), dtype=np.float32)

u2 = np.array([6.262, 2.872])
o2 = 3*np.array([[0.33055867, 0.113388],
                 [0.113388, 0.12050267]])
a2 = (pos-u2).dot(np.linalg.inv(o2))
b2 = np.expand_dims(pos-u2,axis=3)
Z2 = np.zeros((num,num), dtype=np.float32)

for i in range(num):
    Z1[i] = [np.dot(a1[i,j],b1[i,j]) for j in range(num)]
    Z2[i] = [np.dot(a2[i,j],b2[i,j]) for j in range(num)]
Z1 = np.exp(Z1*(-0.5))/(2*np.pi*np.linalg.det(o1))
Z2 = np.exp(Z2*(-0.5))/(2*np.pi*np.linalg.det(o1))

Z = Z1 + Z2

fig = plt.figure()
ax = fig.add_subplot(211,projection='3d')
ax.plot_surface(X, Y, Z, rstride=5, cstride=5, alpha=0.5, cmap=mpl.cm.rainbow)

ax.contour(X,Y,Z1,10,zdir='z',offset=0,cmap=cm.coolwarm)
ax.contour(X,Y,Z2,10,zdir='z',offset=0,cmap=cm.coolwarm)
ax.contour(X, Y, Z, zdir='x', offset=-0,cmap=mpl.cm.winter)
ax.contour(X, Y, Z, zdir='y', offset= 10,cmap= mpl.cm.winter)
'''
mpl.cm.rainbow
mpl.cm.winter
mpl.cm.bwr  # 蓝，白，红
cm.coolwarm
'''

ax.set_xlabel('X')
ax.set_ylabel('Y')
ax.set_zlabel('Z')
plt.show()

ax2 = fig.add_subplot(212)
cs = ax2.contour(X,Y,Z1)
ax2.clabel(cs, inline=1, fontsize=20)
cs2 = ax2.contour(X,Y,Z2)
ax2.clabel(cs2, inline=1, fontsize=20)

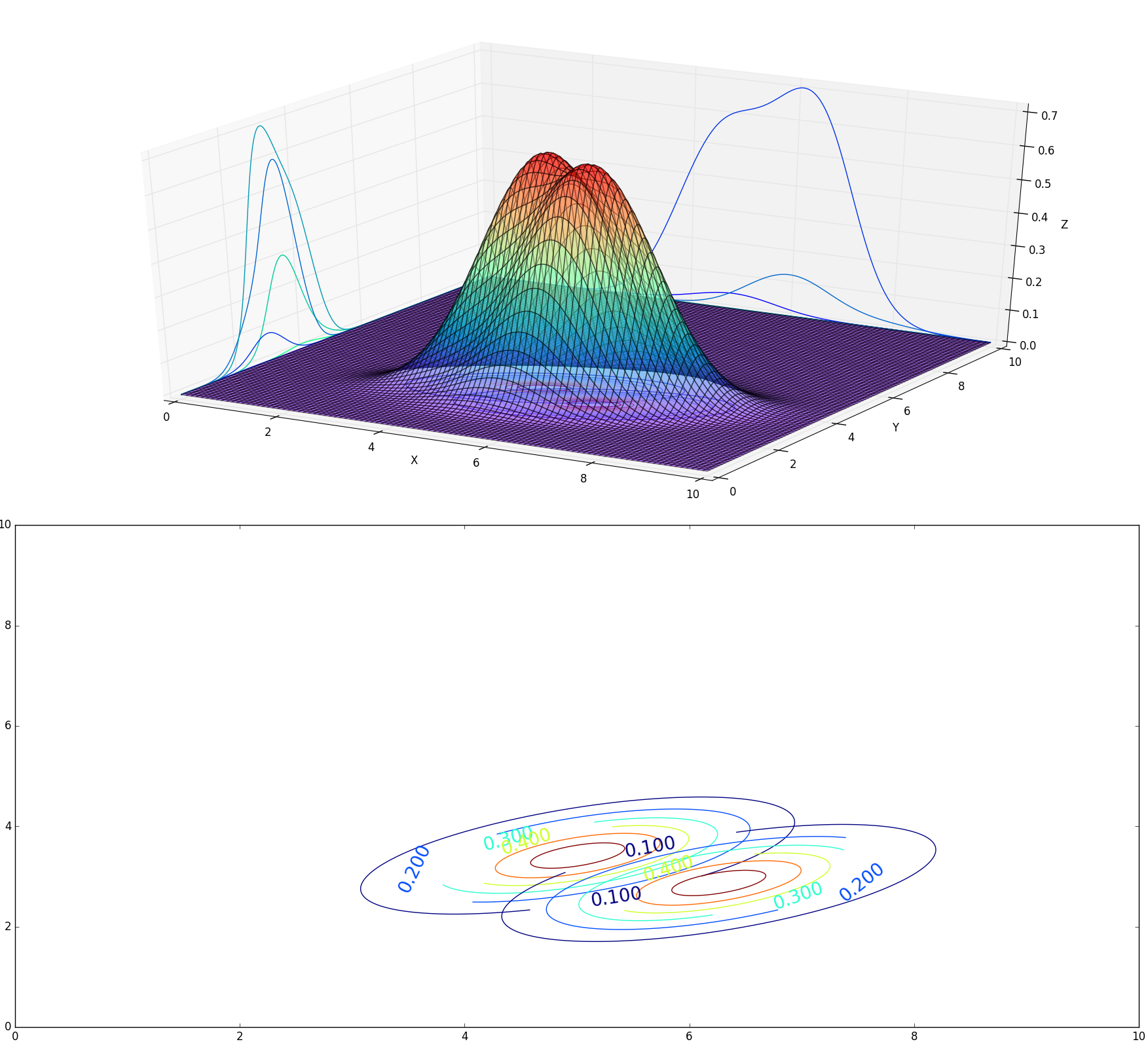
输出图像如下（调整了一下坐标显示，要不然显示不全），

换了个颜色233，

posted @ 2017-09-29 11:00 叠加态的猫阅读(759) 评论(0) 编辑收藏举报

叠加态的猫

『科学计算』高斯判别分析模型实现

公告