『科学计算_理论』优化算法:梯度下降法&牛顿法
梯度下降法
梯度下降法用来求解目标函数的极值。这个极值是给定模型给定数据之后在参数空间中搜索找到的。迭代过程为:
可以看出,梯度下降法更新参数的方式为目标函数在当前参数取值下的梯度值,前面再加上一个步长控制参数alpha。梯度下降法通常用一个三维图来展示,迭代过程就好像在不断地下坡,最终到达坡底。为了更形象地理解,也为了和牛顿法比较,这里我用一个二维图来表示:
懒得画图了直接用这个展示一下。在二维图中,梯度就相当于凸函数切线的斜率,横坐标就是每次迭代的参数,纵坐标是目标函数的取值。每次迭代的过程是这样:
- 首先计算目标函数在当前参数值的斜率(梯度),然后乘以步长因子后带入更新公式,如图点所在位置(极值点右边),此时斜率为正,那么更新参数后参数减小,更接近极小值对应的参数。
- 如果更新参数后,当前参数值仍然在极值点右边,那么继续上面更新,效果一样。
- 如果更新参数后,当前参数值到了极值点的左边,然后计算斜率会发现是负的,这样经过再一次更新后就会又向着极值点的方向更新。
根据这个过程我们发现,每一步走的距离在极值点附近非常重要,如果走的步子过大,容易在极值点附近震荡而无法收敛。解决办法:将alpha设定为随着迭代次数而不断减小的变量,但是也不能完全减为零。
梯度下降法实战
我们来求解Ax=b,程序如下:
%matplotlib inline
import copy
import numpy as np
import matplotlib.pyplot as plt
A = np.array([[4,2],[1,3]])
b = np.array([[3],[2]])
loss = []
x0 = [copy.deepcopy([]), copy.deepcopy([])]
step = 0.01
x = [[0.],[4]]
while (A.dot(x)-b).T.dot(A.dot(x)-b) > 0.1:
dx = 2*A.T.dot(A).dot(x) - 2*A.T.dot(b)
x = x - step*dx
x0[0].append(x[0])
x0[1].append(x[1])
loss.append(np.squeeze((A.dot(x)-b).T.dot(A.dot(x)-b)))
line = np.linspace(0,len(x0[0])-1,len(x0[0]))
fig,(ax0,ax1)=plt.subplots(2,1, figsize=(9,6))
ax1.plot(line, x0[0])
ax1.plot(line, x0[1])
ax0.plot(line, loss)
ax1.plot(line, np.ones(len(x0[0]))*0.5)
plt.show
上图表示loss函数的降低趋势,下图反映了解的收敛趋势:

牛顿法
首先得明确,牛顿法是为了求解函数值为零的时候变量的取值问题的,具体地,
一阶方法:
当要求解 f(θ)=0时,如果 f可导,那么可以通过迭代公式
来迭代求得最小值。通过一组图来说明这个过程。
二阶方法:
当应用于求解最大似然估计的值时,变成ℓ′(θ)=0的问题。这个与梯度下降不同,梯度下降的目的是直接求解目标函数极小值,而牛顿法则变相地通过求解目标函数一阶导为零的参数值,进而求得目标函数最小值。那么迭代公式写作:
当θ是向量时,牛顿法可以使用下面式子表示:
其中H叫做海森矩阵,其实就是目标函数对参数θ的二阶导数。
通过比较牛顿法和梯度下降法的迭代公式,可以发现两者及其相似。海森矩阵的逆就好比梯度下降法的学习率参数alpha。牛顿法收敛速度相比梯度下降法很快,而且由于海森矩阵的的逆在迭代中不断减小,起到逐渐缩小步长的效果。
牛顿法的缺点就是计算海森矩阵的逆比较困难,消耗时间和计算资源。因此有了拟牛顿法。

实践练习

%matplotlib inline
import copy
import numpy as np
from matplotlib import cm
from mpl_toolkits.mplot3d import Axes3D
A = np.array([[4,2],[1,3]])
b = np.array([[3],[2]])
X, Y = np.meshgrid(np.linspace(-10, 10, 200),np.linspace(-10, 10, 200))
def get_loss(X,Y):
Z = (A[0,0]**2+A[1,0]**2)*X**2 + (A[0,1]**2+A[1,1]**2)*Y**2 - 2*(A[0,0]*A[0,1]+A[1,0]*A[1,1])*X*Y - 2*(A[0,0]*b[0]+A[1,0]*b[1])*X \
- 2*(A[0,1]*b[0]+A[1,1]*b[1])*Y
return Z
Z = get_loss(X,Y)
fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')
ax.plot_surface(X,Y,Z,rstride=5, cstride=5, alpha=0.3)
ax.contour(X,Y,Z, alpha=0.3)
cset = ax.contour3D(X, Y, Z, 10, zdir='z', offset=-100, cmap=cm.coolwarm)
# 梯度下降法
step = 0.01
x_g = np.array([[0],[-4]])
for i in range(100):
dx_g = 2*A.T.dot(A).dot(x_g[:,-1].reshape(2,1)) - 2*A.T.dot(b)
x_g = np.concatenate((x_g,x_g[:,-1].reshape(2,1) - step*dx_g),axis=1)
z_g = get_loss(x_g[0],x_g[1])
ax.plot(x_g[0],x_g[1],z_g,'ro')
# 牛顿法
# 黑塞矩阵
H = np.matrix([[A[0,0]**2+A[1,0]**2, A[0,0]*A[0,1]+A[1,0]*A[1,1]],
[A[0,0]*A[0,1]+A[1,0]*A[1,1], A[0,1]**2+A[1,1]**2]],dtype='float64') * 2
x_n = np.array([[0.],[-4.]])
for i in range(100):
dx_n = 2*A.T.dot(A).dot(x_n[:,-1].reshape(2,1)) - 2*A.T.dot(b)
x_n = np.concatenate((x_n, x_n[:,-1] - np.linalg.inv(H).dot(dx_n)),axis=1)
z_n = get_loss(np.squeeze(np.asarray(x_n[0])),np.squeeze(np.asarray(x_n[1])))
ax.plot(np.squeeze(np.asarray(x_n[0])),np.squeeze(np.asarray(x_n[1])),z_n,'go')
f, (ax1, ax2) = plt.subplots(1, 2)
ax1.plot(np.linspace(0,len(z_g)-1,len(z_g)),z_g,'b',label='grad')
ax1.plot(np.linspace(0,len(z_n)-1,len(z_n)),z_n,'r',label='Newton')
ax1.legend()
cs = ax2.contour(X,Y,Z)
ax2.clabel(cs, inline=1, fontsize=5)
ax2.plot(np.squeeze(np.asarray(x_n[0])),np.squeeze(np.asarray(x_n[1])),'b')
ax2.plot(x_g[0],x_g[1],'r')
程序学习:
尝试了平面等高线图和线标注的绘制,
cs = ax2.contour(X,Y,Z)
ax2.clabel(cs, inline=1, fontsize=5)
注意到数组拼接方法都是不破坏原数组,单纯返回新数组的,且axis=0是行拼接(行数增加),axis=1是列拼接(列数增加),
x_n = np.concatenate((x_n, x_n[:,-1] - np.linalg.inv(H).dot(dx_n)),axis=1)
学习了numpy中的矩阵类型:np.matrix(),在牛顿法中我用的是matrix,在梯度下降法中我用的是array:
matrix是array的子类,特点是有且必须只是2维,matrix.I()可以求逆,和线代的求逆方法一致,所以绘图时我不得不才用np.sequeeze(np.asarray())操作来降维,而由于x[:, -1]这种操作对array会自动降维(由两行变为一行),所以要么使用matrix,要么切片后reshape(2,1),总之不消停。
结果分析:
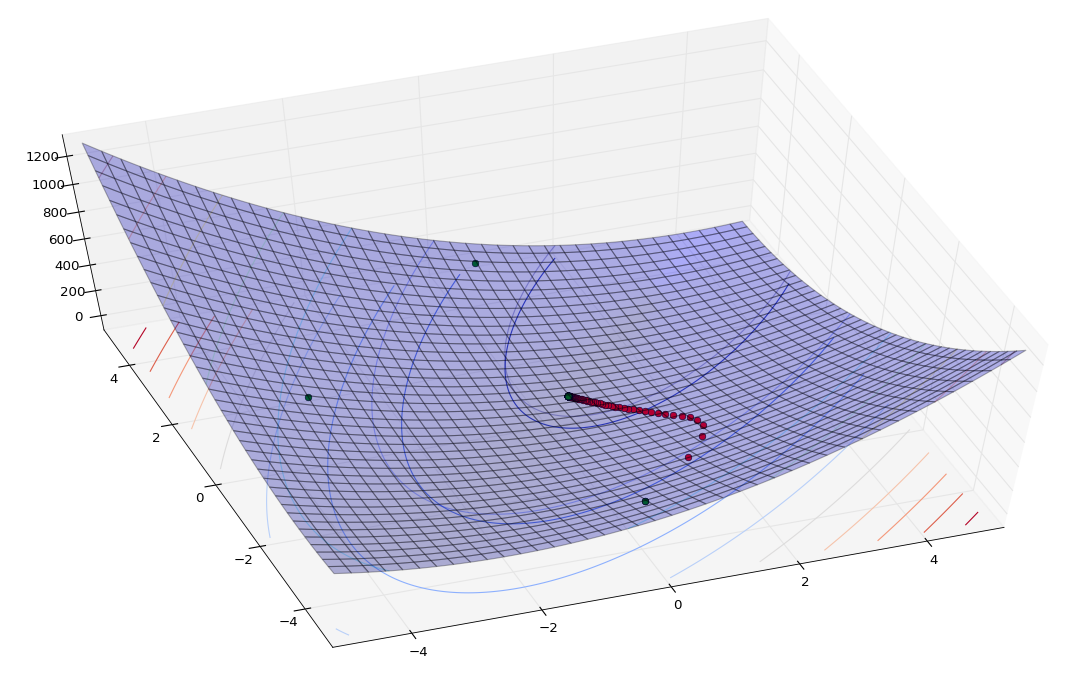
从两张角度截一下图,红色是梯度下降蓝色是牛顿法,可以看到,牛顿法收敛速度很快(外围只有3个点),不过这是建立在黑塞矩阵的基础上(需要求解目标函数的二阶偏导数),这是牛顿法快速收敛的原因,也是牛顿法的瓶颈,而且这个瓶颈很直观:我计算黑塞矩阵的numpy矩阵表达方法时的确费了挺大劲(其实原因更多是我渣... ...)








 浙公网安备 33010602011771号
浙公网安备 33010602011771号