Syntax-Aware Network for Handwritten Mathematical Expression Recognition
A Tree-Structured Decoder for Image-to-Markup Generation（https://www.zhuanzhi.ai/document/f09d28ca52b77a13a13bf44a86aba64d）
Handwritten Mathematical Expression Recognition via Attention Aggregation based Bi-directional Mutual Learning
思路概览
和A Tree-Structured Decoder for Image-to-Markup Generation思路一致，看起来是为了数学公式增加了一些细致的规则。
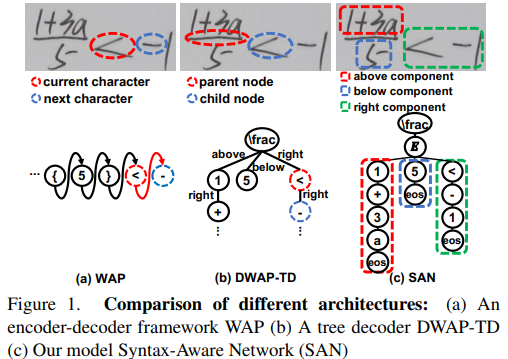
SAN的工作本质原文描述如下：
The SAN transforms an image into a parse tree, of which the leaf nodes are terminal symbols or relations, and others are non-terminal symbols. There are two non-terminal symbols S and E, where S is the start symbol and servers as the tree’s root.
作者将SAN分成七个组件，G = (N, Σ, R, S, Γ, C, D)：
- a finite set of nonterminal symbols (N),
- 实际latex符号 a finite set of terminal symbols (Σ, non-terminal symbols), contains all symbols that might be used in a LaTeX expression sequence.
- 建树规则 a finite set of production rules (R), production rule can be used to construct the parse tree.
- 子树起始符，这个应该属于N a start symbol (S, non-terminal symbols), is the start symbol and servers as the tree’s root.
- 关系符号 a finite set of relations (Γ),
- an encoder (C)
- a decoder (D).
父节点类型N（非终端节点）根据生成规则R可以生成一系列终端Σ、非终端N、关系Γ子节点。
建树规则
非终端符号S产生：
1) an arbitrary terminal symbol followed by an S on the right
2) an E
3) an empty string
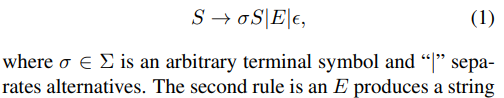
非终端符号E对Γ中的每种关系产生一个子树，并将这些子树concat起来
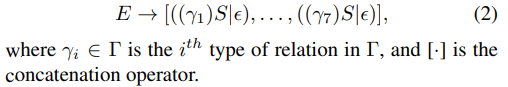
看到这里就大概明白了作者的意图，起始S符号，然后：
- 输出σS，表示当前位置为符号σ，下一个S输出修饰σ的子树
- 输出E，表示修饰S兄弟符号σ，递归预测
- 输出空，表示S的兄弟符号无需修饰
对于某个字符的关联字符（E位置），节点子树为修饰用，对各种可能的关系进行探索，各个关系平级（结果之间concat）。
下图是生成树的规则示意：
节点推理该率分布表达如下（父节点到子节点，X为图）：
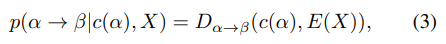
相邻符号有九种可能关系：left, right, above, below, low left, low right, upper left, upper right（？）
Latex语法树生成的两个原则：
- It follows the standard reading orders: left-to-right, top-to-down.
- The spatial relations between adjacent symbols are used. 相邻符号之间存在关系符号
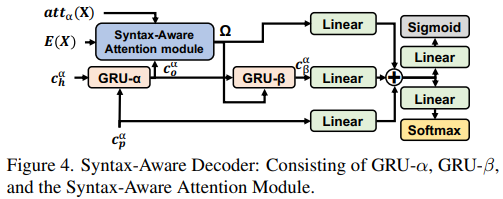
解码过程
