『论文笔记』Swin Transformer
https://zhuanlan.zhihu.com/p/361366090
目前transform的两个非常严峻的问题
- 受限于图像的矩阵性质，一个能表达信息的图片往往至少需要几百个像素点，而建模这种几百个长序列的数据恰恰是Transformer的天生缺陷；
- 目前的基于Transformer框架更多的是用来进行图像分类，对实例分割这种密集预测的场景Transformer并不擅长解决。
在Swin Transformer之前的ViT和iGPT，它们都使用了小尺寸的图像作为输入，这种直接resize的策略无疑会损失很多信息。与它们不同的是，Swin Transformer的输入是图像的原始尺寸另外Swin Transformer使用的是CNN中最常用的层次的网络结构，在CNN中一个特别重要的一点是随着网络层次的加深，节点的感受野也在不断扩大，这个特征在Swin Transformer中也是满足的。Swin Transformer的这种层次结构，也赋予了它可以像FPN，U-Net等结构实现可以进行分割或者检测的任务。
图1：Swin Transformer和ViT的对比
图2：Swin-T的网络结构
Patch Partition/Patch Merging
在图2中，输入图像之后是一个Patch Partition，再之后是一个Linear Embedding层，这两个加在一起其实就是一个Patch Merging层（至少上面的源码中是这么实现的）。这一部分的源码如下：
class PatchMerging(nn.Module):
def __init__(self, in_channels, out_channels, downscaling_factor):
super().__init__()
self.downscaling_factor = downscaling_factor
self.patch_merge = nn.Unfold(kernel_size=downscaling_factor, stride=downscaling_factor, padding=0)
self.linear = nn.Linear(in_channels * downscaling_factor ** 2, out_channels)
def forward(self, x):
b, c, h, w = x.shape
new_h, new_w = h // self.downscaling_factor, w // self.downscaling_factor
x = self.patch_merge(x) # (1, 48, 3136)
x = x.view(b, -1, new_h, new_w).permute(0, 2, 3, 1) # (1, 56, 56, 48)
x = self.linear(x) # (1, 56, 56, 96)
return x
Patch Merging的作用是对图像进行降采样，类似于CNN中Pooling层。Patch Merging是主要是通过nn.Unfold函数实现降采样的，nn.Unfold的功能是对图像进行滑窗，相当于卷积操作的第一步，因此它的参数包括窗口的大小和滑窗的步长。根据源码中给出的超参我们知道这一步降采样的比例是 ，因此经过
nn.Unfold之后会得到 个长度为
的特征向量，其中
是输入到这个stage的Feature Map的通道数，第一个stage的输入是RGB图像，因此通接着的
view和permute是将得到的向量序列还原到 的二维矩阵，
linear是将长度是 的特征向量映射到
out_channels的长度，因此stage-1的Patch Merging的输出向量维度是 ，对比源码的注释，这里省略了第一个batch为
的维度。
可以看出Patch Partition/Patch Merging起到的作用像是CNN中通过带有步长的滑窗来降低分辨率，再通过 卷积来调整通道数。不同的是在CNN中最常使用的降采样的最大池化或者平均池化往往会丢弃一些信息，例如最大池化会丢弃一个窗口内的地响应值，而Patch Merging的策略并不会丢弃其它响应，但它的缺点是带来运算量的增加。在一些需要提升模型容量的场景中，我们其实可以考虑使用Patch Merging来替代CNN中的池化。
作用就是更好的降采样，CNN中最常使用的降采样的最大池化或者平均池化往往会丢弃一些信息，例如最大池化会丢弃一个窗口内的地响应值，而Patch Merging的策略并不会丢弃其它响应，但它的缺点是带来运算量的增加。
Swin Transformer的Stage
Swin Transformer的一个stage便可以看做由Patch Merging和Swin Transformer Block组成，
class StageModule(nn.Module):
def __init__(self, in_channels, hidden_dimension, layers, downscaling_factor, num_heads, head_dim, window_size,
relative_pos_embedding):
super().__init__()
assert layers % 2 == 0, 'Stage layers need to be divisible by 2 for regular and shifted block.'
self.patch_partition = PatchMerging(in_channels=in_channels, out_channels=hidden_dimension,
downscaling_factor=downscaling_factor)
self.layers = nn.ModuleList([])
for _ in range(layers // 2):
self.layers.append(nn.ModuleList([
SwinBlock(dim=hidden_dimension, heads=num_heads, head_dim=head_dim, mlp_dim=hidden_dimension * 4,
shifted=False, window_size=window_size, relative_pos_embedding=relative_pos_embedding),
SwinBlock(dim=hidden_dimension, heads=num_heads, head_dim=head_dim, mlp_dim=hidden_dimension * 4,
shifted=True, window_size=window_size, relative_pos_embedding=relative_pos_embedding),
]))
def forward(self, x):
x = self.patch_partition(x)
for regular_block, shifted_block in self.layers:
x = regular_block(x)
x = shifted_block(x)
return x.permute(0, 3, 1, 2)由窗口多头自注意层（window multi-head self-attention, W-MSA）和移位窗口多头自注意层（shifted-window multi-head self-attention, SW-MSA）组成，如图3所示。由于这个原因，Swin Transformer的层数要为2的整数倍，一层提供给W-MSA，一层提供给SW-MSA。
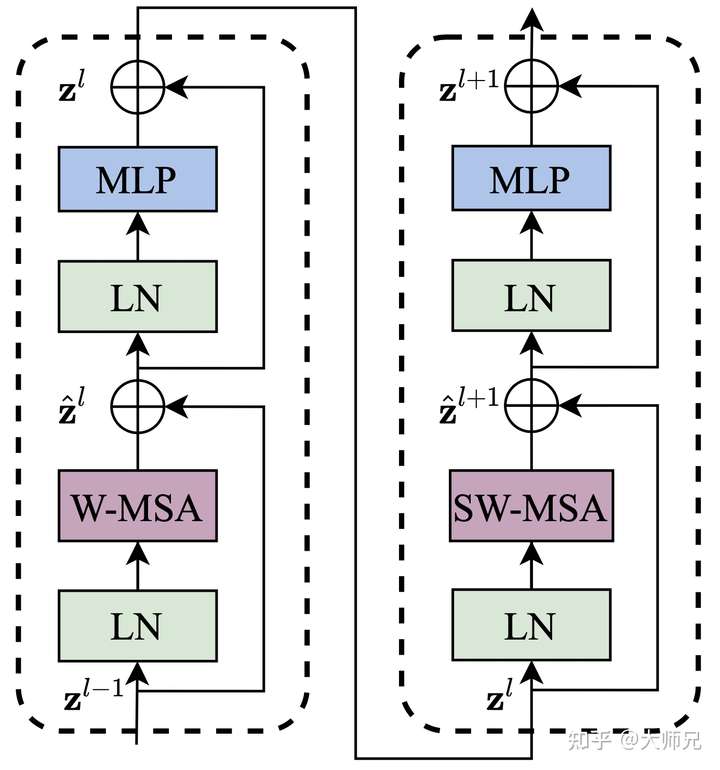图3：Swin Transformer Block的网络结构
从图3中我们可以看出输入到该stage的特征 先经过LN进行归一化，再经过W-MSA进行特征的学习，接着的是一个残差操作得到
。接着是一个LN，一个MLP以及一个残差，得到这一层的输出特征
。SW-MSA层的结构和W-MSA层类似，不同的是计算特征部分分别使用了SW-MSA和W-MSA，可以从上面的源码中看出它们除了
shifted的这个bool值不同之外，其它的值是保持完全一致的。这一部分可以表示为式(2)。
一个Swin Block的源码如下所示，和论文中图不同的是，LN层（PerNorm函数）从Self-Attention之前移到了Self-Attention之后。
class Residual(nn.Module):
def __init__(self, fn):
super().__init__()
self.fn = fn
def forward(self, x, **kwargs):
return self.fn(x, **kwargs) + x
class PreNorm(nn.Module):
def __init__(self, dim, fn):
super().__init__()
self.norm = nn.LayerNorm(dim)
self.fn = fn
def forward(self, x, **kwargs):
return self.fn(self.norm(x), **kwargs)
class SwinBlock(nn.Module):
def __init__(self, dim, heads, head_dim, mlp_dim, shifted, window_size, relative_pos_embedding):
super().__init__()
self.attention_block = Residual(PreNorm(dim, WindowAttention(dim=dim, heads=heads, head_dim=head_dim, shifted=shifted, window_size=window_size, relative_pos_embedding=relative_pos_embedding)))
self.mlp_block = Residual(PreNorm(dim, FeedForward(dim=dim, hidden_dim=mlp_dim)))
def forward(self, x):
x = self.attention_block(x)
x = self.mlp_block(x)
return x窗口多头自注意力（Window Multi-head Self Attention，W-MSA）
顾名思义，就是个在窗口的尺寸上进行Self-Attention计算，与SW-MSA不同的是，它不会进行窗口移位，它们的源码如下。我们这里先忽略shifted为True的情况
class WindowAttention(nn.Module):
def __init__(self, dim, heads, head_dim, shifted, window_size, relative_pos_embedding):
super().__init__()
inner_dim = head_dim * heads
self.heads = heads
self.scale = head_dim ** -0.5
self.window_size = window_size
self.relative_pos_embedding = relative_pos_embedding # (13, 13)
self.shifted = shifted
if self.shifted:
displacement = window_size // 2
self.cyclic_shift = CyclicShift(-displacement)
self.cyclic_back_shift = CyclicShift(displacement)
self.upper_lower_mask = nn.Parameter(create_mask(window_size=window_size, displacement=displacement, upper_lower=True, left_right=False), requires_grad=False) # (49, 49)
self.left_right_mask = nn.Parameter(create_mask(window_size=window_size, displacement=displacement,pper_lower=False, left_right=True), requires_grad=False) # (49, 49)
self.to_qkv = nn.Linear(dim, inner_dim * 3, bias=False)
if self.relative_pos_embedding:
self.relative_indices = get_relative_distances(window_size) + window_size - 1
self.pos_embedding = nn.Parameter(torch.randn(2 * window_size - 1, 2 * window_size - 1))
else:
self.pos_embedding = nn.Parameter(torch.randn(window_size ** 2, window_size ** 2))
self.to_out = nn.Linear(inner_dim,