『论文笔记』Connectionist Temporal Classification with Maximum Entropy Regularization
https://zhuanlan.zhihu.com/p/82302872
CTC的问题:
1、容易陷入局部最优
2、尖峰分布

作者认为peak distribution是一种过拟合的表现,
However, CTC tends to produce highly peaky and overconfident distributions, which is a symptom of overfitting.
由于CTC可以认为是多实例学习的一种,CTC中的标签事件可以看做是所有可行路径的包(即多条路径经过many-to-one操作后输出相同的字符串):
CTC can be regarded as a kind of Multiple Instance Learning (MIL). From the perspective of MIL, the label sequence is a bag containing all feasible paths.
如果某条路径的概率较大,那么CTC会加强该路径直至占有所有路径的绝大部分,是一种正向激励的作用。且由于blank在多数路径都存在,blank也会加强,直至充满主要路径,使得non-blank labels只占有尖峰,即CTC尖峰分布问题:
As blanks are included in most of the feasible paths, dominant paths are often overwhelmed by blanks, interspersed by sharp spikes (narrow regions along the time axis) of non-blank labels, which is known as the CTC peaky distribution problem.
这种现象会带来很多问题:
- Harm the training process.对路径的正向激励导致网络容易陷入局部最小值之中。
- Output overconfident paths.尖峰的存在在某些应用场景不适合,比如语音识别中的相邻音节,另外,较低的熵也可以看做是过拟合的一种。
- Output paths with peaky distribution.尖峰的存在不适合序列分割任务。
EnCTC
论文提出了基于最大熵的正则化方法EnCTC去抑制最大概率路径的存在:
To remedy this, we propose a regularization method based on maximum conditional entropy which penalizes peaky distributions and encourages exploration.
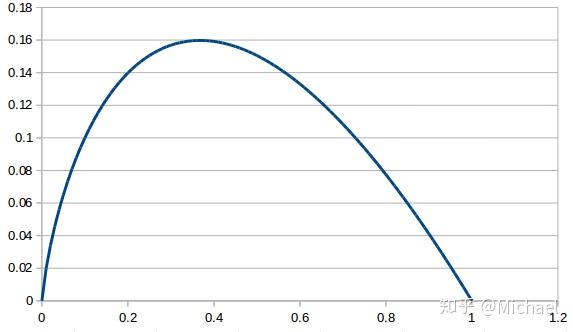
最大熵的公式为
由于 在
区间的曲线为:
CTC的损失函数为:
其中, 。
梯度为:
由于只有部分路径包含 ,所以只需要考虑包含
的部分路径对
的偏导即可。
而 ,因此有:
论文认为上式可以推导出 的梯度与经过该点所有路径的概率(即
)之和相关,且概率与梯度成正比关系,论文认为这是导致尖峰存在的原因:
We can see that the error signal is proportional to the fraction of all feasible paths that go through symbolat time
. That means once a feasible path is dominant, the error signal of
will dominate
at all time-steps
, causing all the probabilities to focus on a single path while ignoring its alternatives.
论文在损失函数里加入了最大熵部分:
其中, 。
论文发现在该损失部分概率接近0的路径贡献了损失的大部分(这里论文推导了一些公式,如果有兴趣可查看论文),这对训练的多样性是有用的:
Therefore, paths with probability between 0 and, i.e. paths near the the dominant path, contribute the most to the error signal. This error signal will in turn increase the probability of the nearby paths and improve the exploration during training.

EsCTC
由于ctc的gt是近似等间隔的,作者希望利用这个性质约束可行路径

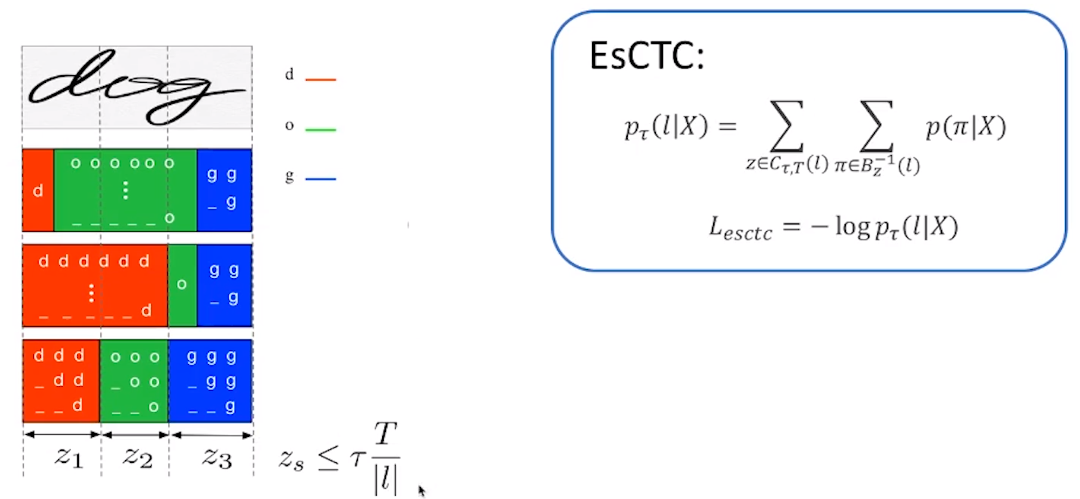
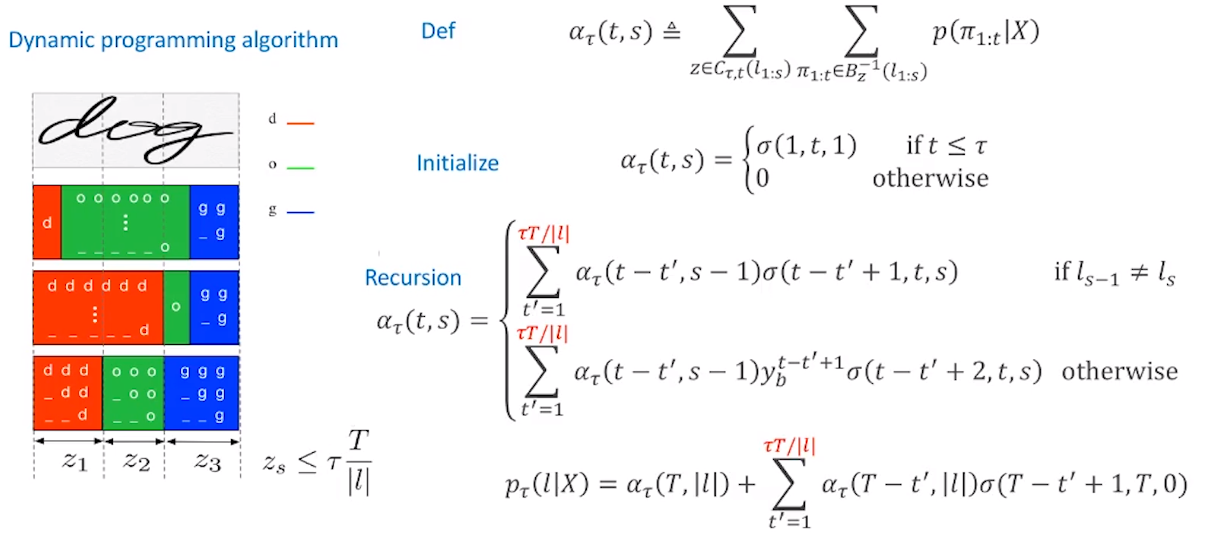
同样给出了动态规划算法,先计算每一小段的概率:

输出s小段的概率,初始化第一行表示第一小段内部直接沿用上面slice的结果:
为啥这个也交最大熵:
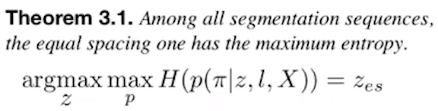




 浙公网安备 33010602011771号
浙公网安备 33010602011771号