『计算机视觉』Generalized Intersection over Union: A Metric and A Loss for Bounding BoxRegression
论文地址：Generalized Intersection over Union
一、相关工作
目标检测精度标准
度量检测优劣基本基于 IOU，mAP 是典型的基于 IOU 的标准，但是 mAP 仅有一个 threshold，对于过了线的预测框一视同仁，不能进一步衡量其优劣，所以 MS COCO 挑战赛提出了多 IOU 阈值的综合 mAP 评价标准（就是同时采用几个阈值，计算出多个 mAP 综合打分）。
Bounding box 表示方法和损失函数
YOLO v1 直接回归 bbox 的位置参数（x，y，h，w），并在（h，w）采用预测平方根的方式回避尺度敏感
RCNN 预测的是相对预先检测出的候选区的位置偏移，采用 log 空间回避尺度敏感
此时的损失函数以 l2 为主
Faster RCNN 提出 l1 smooth 损失函数，使得学习鲁棒性更好
Faster RCNN 提出了 anchor boxes 取代了 RCNN 系列中的候选生成算法，但是过多的 anchor 候选框导致了正负样本不平衡的问题，其作者进一步提出了 focal loss 进行应对（存疑，一般来说 one stage 法更易受到正负样本不平衡的困扰，而 two stage 法由于会在候选框阶段通过得分和nms筛选过滤掉大量的负样本，然后在分类回归阶段又固定正负样本比例，相较 one stage 法情况会好很多）。
二、Generalized Intersection over Union
1、IOU 的优点
- 将 1-IOU 作为距离度量，（数学可证的）满足非负性、同一性、对称性和三角不等性（non-negativity, identity of indiscernibles, symmetry and triangle inequality）
- IOU 具有尺度不变性，不受 bbox 于 ground truth 的大小影响
2、IOU 的问题
- 只要两个框不相交，IOU 就为0，这使得它无法衡量两个框是相邻还是相距甚远
- IOU 无法反映两个框相交的方式，解释如 Figure2 所示：
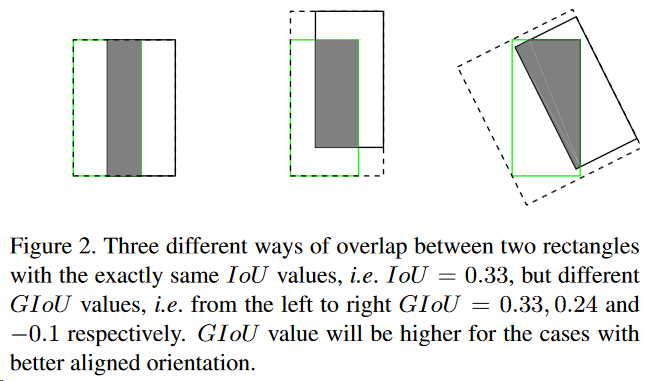
3、GIOU 算法介绍
对于同形状的 A 和 B，C 为相同形状的最小的可以包含 A、B 的图形（例如通常 A 和 B 是矩形框，此时 C 也取矩形框），下面公式给出 GIOU 的计算过程：
然后作者给出了 GIOU 的5个特点：
- 将 1-GIOU 作为距离度量，其继承了 IOU 的优良数学特性
- GIOU 同样具有尺度不变性
- GIOU 永远小于 IOU，且当 A 趋近于 B 时（即两者趋于重合），GIOU 趋于 IOU
- IOU 取值区间为 [0，1]，GIOU 取值区间为 [-1，1]：
和 3 中所说对应，A 和 B 趋于重合时 IOU 和 GIOU 均趋向 1
A 和 B 差别越大，GIOU 趋向于 -1 - 如 Figure2 所示，GIOU 相对 IOU 更能反映两个框相交形式的好坏（how overlap between two symmetrical objectsoccurs）
4、GIOU 应用为损失函数
基于 min、max 和 分段函数的BP算法是可行的，所以 IOU 与 GIOU 的应用就不是问题了。作者说，虽然 IOU（GIOU） 计算不能得到解析解，但在限定了形状为矩形时就大大简化了问题：对角点进行 min、max 操作即可：
作者还画了图试图证明 GIOU 损失函数的梯度相对于 IOU 损失函数更大，不过我感觉有点牵强（没看懂），所以不贴了。
三、实验
作者将 GIOU 损失函数应用到已有 2D 物体检测算法中，结果相对从前在两个指标上：IOU、GIOU 均有提高，毕竟优化目标就是检测指标，比起使用中间量的 l2 损失效果好是情理之中的。
文章源码还没有被释放，不过原理并不复杂，只要修改已有算法的损失函数即可，但是最近比较忙，没有时间实践一下了。个人觉得是篇很中肯的文章，期待其他人复现实验验证一下，如果效果好说不定就像 BN、Relu 一样成为相关领域的标准配置了。
