『教程』Batch Normalization 层介绍
思考
YJango的前馈神经网络--代码LV3的数据预处理中提到过:在数据预处理阶段,数据会被标准化(减掉平均值、除以标准差),以降低不同样本间的差异性,使建模变得相对简单。
我们又知道神经网络中的每一层都是一次变换,而上一层的输出又会作为下一层的输入继续变换。如下图中, 经过第一层
的变换后,所得到的
; 而
经过第二层
的变换后,得到
。
在第二层所扮演的角色就是
在第一层所扮演的角色。 我们将
进行了标准化,那么,为什么不对
也进行标准化呢?
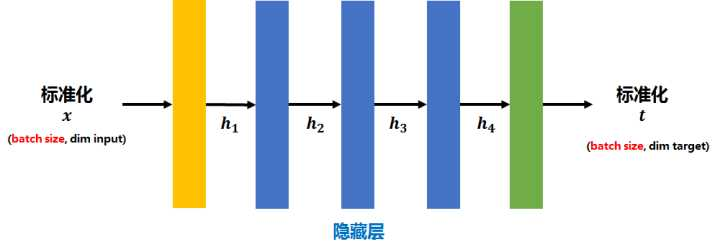
Batch Normalization论文便首次提出了这样的做法。
Batch Normalization(BN)就是将每个隐藏层的输出结果(如 )在batch上也进行标准化后再送入下一层(就像我们在数据预处理中将
进行标准化后送入神经网络的第一层一样)。
优点
那么Batch Normalization(BN)有什么优点?BN的优点是多个并存,但这里只提一个最容易理解的优点。
训练时的问题
尽管在讲解神经网络概念的时候,神经网络的输入指的是一个向量 。
但在实际训练中有:
- 随机梯度下降法(Stochastic Gradient Descent):用一个样本的梯度来更新权重。
- 批量梯度下降法(Batch Gradient Descent):用多个样本梯度的平均值来更新权重。
如下图所示,绿、蓝、黑的箭头表示三个样本的梯度更新网络权重后loss的下降方向。
若用多个梯度的均值来更新权重的批量梯度下降法可以用相对少的训练次数遍历完整个训练集,其次可以使更新的方向更加贴合整个训练集,避免单个噪音样本使网络更新到错误方向。
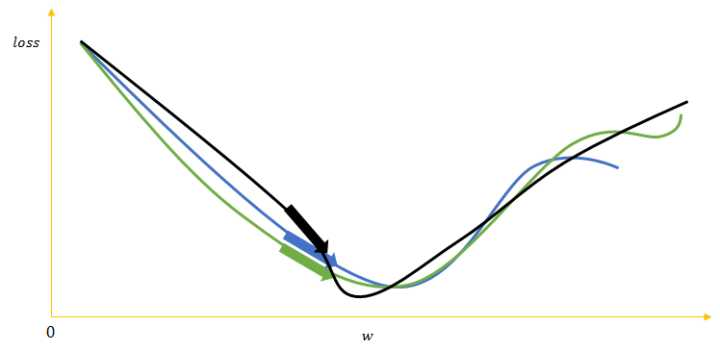
然而也正是因为平均了多个样本的梯度,许多样本对神经网络的贡献就被其他样本平均掉了,相当于在每个epoch中,训练集的样本数被缩小了。batch中每个样本的差异性越大,这种弊端就越严重。
一般的解决方法就是在每次训练完一个epoch后,将训练集中样本的顺序打乱再训练另一个epoch,不断反复。这样重新组成的batch中的样本梯度的平均值就会与上一个epoch的不同。而这显然增加了训练的时间。
同时因为没办法保证每次更新的方向都贴合整个训练集的大方向,只能使用较小的学习速率。这意味着训练过程中,一部分steps对网络最终的更新起到了促进,一部分steps对网络最终的更新造成了干扰,这样“磕磕碰碰”无数个epoch后才能达到较为满意的结果。
注:一个epoch是指训练集中的所有样本都被训练完。一个step或iteration是指神经网络的权重更新一次。
为了解决这种“不效率”的训练,BN首先是把所有的samples的统计分布标准化,降低了batch内不同样本的差异性,然后又允许batch内的各个samples有各自的统计分布。所以,
BN的优点自然也就是允许网络使用较大的学习速率进行训练,加快网络的训练速度(减少epoch次数),提升效果。
做法
设,每个batch输入是 (其中每个
都是一个样本,
是batch size) 假如在第一层后加入Batch normalization layer后,
的计算就倍替换为下图所示的那样。

- 矩阵
先经过
的线性变换后得到
- 注:因为减去batch的平均值
后,
的作用会被抵消掉,所以没必要加入
(红色删除线)。
- 将
再减去batch的平均值
,并除以batch的标准差
得到
。
是为了避免除数为0的情况所使用的微小正数。
- 注:但
基本会被限制在正态分布下,使得网络的表达能力下降。为解决该问题,引入两个新的parameters:
和
。
和
是在训练时网络自己学习得到的。
- 将
乘以
调整数值大小,再加上
增加偏移后得到
。
- 为加入非线性能力,
也会跟随着ReLU等激活函数。
- 最终得到的
会被送到下一层作为输入。
需要注意的是,上述的计算方法用于在训练。因为测试时常会只预测一个新样本,也就是说batch size为1。若还用相同的方法计算 ,
就会是这个新样本自身,
就会成为0。
所以在测试时,所使用的 和
是整个训练集的均值
和方差
。
而整个训练集的均值和方差
的值通常也是在训练的同时用移动平均法来计算,会在下一篇代码演示中介绍。
附带一提,反向传播公式如下:
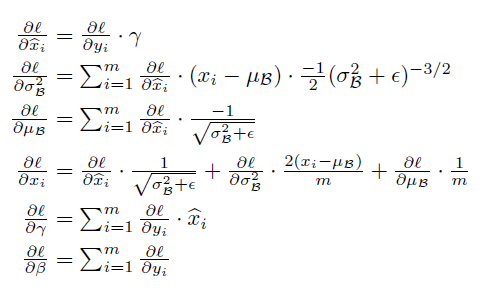




 浙公网安备 33010602011771号
浙公网安备 33010602011771号