ARM DSP库CMSIS-DSP的使用——以STM32F4浮点FFT为例 [原创www.cnblogs.com/helesheng]
之前用过STM32F10x比较多,做数字信号处理用过意法半导体官方的STM32F10x_DSP_Lib_V2.0.0,总觉得这个库不太好用:
1、数字滤波器FIR和IIR的函数只能对存在缓冲中的数组滤波,且没有能够保存滤波器中间状态的数据结构,导致再次调用这些滤波函数时需要一个新的稳定期,无法实现连续实时滤波。
2、只有定点FFT函数,输出结果保存在16bits的定点寄存器中,大大降低了FFT结果的动态范围。
因此我在STM32F10x上总习惯采用自己编写的C语言数字信号处理函数,无论是时间效率还是内存效率都差强人意。
最近在项目中开始使用带有浮点处理单元(FPU)的Cortex-M4核STM32F4,发现ARM公司自己提供的CMSIS(Cortex Microcontroller Software Interface Standard)中的数字信号库(CMSIS-DSP)确实要给力得多。下面以需要浮点能力的FFT功能为例,介绍CMSIS-DSP在MDK环境中的使用。
以下原创内容欢迎网友转载,但请注明出处: https://www.cnblogs.com/helesheng
一、准备工作和准备知识
1、在意法半导体官方网站下载包含CMSIS-DSP的外设库(https://www.st.com/en/embedded-software/stsw-stm32065.html),当然也可以到ARM官方的GitHub账号(https://github.com/ARM-software/CMSIS)下载所有ARM Cortex-M内核的DSP外设库。数字信号库包含在路径STM32F4xx_DSP_StdPeriph_Lib_V1.8.0\Libraries\CMSIS\DSP_Lib和STM32F4xx_DSP_StdPeriph_Lib_V1.8.0\Libraries\CMSIS\Lib下,将它们拷贝到目标工程文件夹下。其中Lib文件夹中包含的是经过不同编译器编译后能够运行在Cortex-M4内核上的底层数学库,DSP_Lib文件夹中包含的是调用底层函数封装而成的API函数源码。
2、Lib文件夹中包含的底层库包括:
arm_cortexM4lf_math.lib
arm_cortexM4bf_math.lib
arm_cortexM4l_math.lib
arm_cortexM4b_math.lib
arm_cortexM3l_math.lib
arm_cortexM3b_math.lib
arm_cortexM0l_math.lib
arm_cortexM0b_math.lib
M0、M3、M4分别代表Cortex-M0、Cortex-M3、Cortex-M4内核上运行的库;字母l代表小端地址格式,b代表大端地址格式(所有STM32皆为小端地址格式处理器);字母f代表使用浮点处理单元(FPU)进行计算的库。例如,我打算使用STM32F4处理器的FPU进行FFT运算,就需要将库文件arm_cortexM4lf_math.lib添加到Keil MDK工程中。
3、DSP_Lib中包含了如下所示的多个文件夹,它们中的文件功能如下:1)BasicMathFunctions
基本数学函数:提供浮点数的各种基本运算函数,如向量加减乘除等运算。
2)CommonTables
数字信号处理常用参数表。
3)ComplexMathFunctions
复数计算数学函数。
4)ControllerFunctions
控制算法函数。包括正弦余弦,PID电机控制,矢量Clarke变换,矢量Clarke逆变换等。
5)FastMathFunctions
常见快速算法的数学函数。
6)FilteringFunctions
滤波函数功能,主要为FIR和LMS(最小均方根)等滤波函数。
7)MatrixFunctions
矩阵处理函数。包括矩阵加法、矩阵初始化、矩阵反、矩阵乘法、矩阵规模、矩阵减法、矩阵转置等函数。
8)StatisticsFunctions
统计功能函数。如求平均值、最大值、最小值、计算均方根RMS、计算方差/标准差等。
9)SupportFunctions
支持功能函数,如数据拷贝,Q格式和浮点格式相互转换,Q任意格式相互转换。
10)TransformFunctions
变换功能。包括复数FFT(CFFT)/复数FFT逆运算(CIFFT)、实数FFT(RFFT)/实数FFT逆运算(RIFFT)、和DCT(离散余弦变换)和配套的初始化函数。
例如,这里我打算通过浮点FFT运算进行频谱分析,就使用了TransformFunctions文件夹下的arm_cfft_f32.c中的函数。
二、配置Keil MDK工程
1、在Options的Target选项卡中使能浮点运算单元FPU。

图1
2、在Options的C/C++选项卡的宏定义中添加如下数学计算可能用到的宏ARM_MATH_CM4,__CC_ARM,ARM_MATH_MATRIX_CHECK,ARM_MATH_ROUNDING。

图2
三、调用DSP_LIB中的函数实现FFT
1、从ARM官方帮助文档中查找合适的函数及其使用方法
ARM官方的CMSIS-DSP库的帮助文档是HTML格式的网页,保存在.. \STM32F4xx_DSP_StdPeriph_Lib_V1.8.0\Libraries\CMSIS路径下,打开后如下图所示。

图3
我选择32位浮点(float)数据类型的函数arm_cfft_f32();来实现FFT,其原型如网页右侧视图所示。
从上面的网页中可以查得:
1 void arm_cfft_f32 ( 2 const arm_cfft_instance_f32 * S, 3 float32_t * p1, 4 uint8_t ifftFlag, 5 uint8_t bitReverseFlag 6 );
函数名称中的字母“c”表明,这个函数的输入和输出都是复数(complex number)。输入复数向量存放在第二个参数p1指向的浮点数组中,函数执行完后输出复数向量亦存放在相同地址。输入输出复数数组的存储结构相同,偶数地址用于存储复数实部,随后的奇数地址用于存储同一个复数的虚部。
第一个参数则是一个指向复数浮点FFT常数结构体的指针,该结构体已经定义在头文件arm_const_structs.h中,可以直接通过&arm_cfft_sR_f32_len256、&arm_cfft_sR_f32_len512、&arm_cfft_sR_f32_len1024等形式应用,FFT变换的点数由改参数决定。
此处注意不要忘记在调用DSP库函数的文件之前添加头文件:#include "arm_const_structs.h"
第三个参数ifftFlag用于指定函数执行的FFT逆变换(ifftFlag=1),还是FFT正变换(ifftFlag=0)。
第四个参数bitReverseFlag用于指定是否对结果进行位翻转变换,根据FFT理论知识可知,对自然顺序输入进行FFT蝶形运算的结果的顺序,是自然顺序输出的地址高低位翻转的结果。当bitReverseFlag=1时,该函数能够对输出的结果执行地址高低位翻转和顺序置换;当bitReverseFlag=0时,该功能被禁止。大多数情况下,为得到频率依次递增的频域数据,需要使能该函数的位翻转功能。
2、调用函数arm_cfft_f32();实现FFT
为验证STM32F4xx_DSP_StdPeriph_Lib中DSP功能调用的正确性,我对STM32F401RC片上ADC采集得到的信号进行了FFT变换和显示。具体实现步骤如下:
1)通过DMA控制ADC实现高速采样,代码如下(其中DMA配置函数ADC_Config();不是本文重点,具体代码此处未列出):
1 ADC_Config();//ADC和DMA配置 2 ADC_SoftwareStartConv(ADCx); //启动adc和DMA传输 3 while(DMA_GetFlagStatus(DMA_STREAMx, DMA_FLAG_TCIF0) == RESET) ; 4 //等待采样和DMA传输完成 5 ADC_DMACmd(ADCx, DISABLE); 6 DMA_ClearFlag(DMA_STREAMx, DMA_FLAG_TCIF0);
2)将采样结果放置在复数结构的缓冲区中。其中数组uhADCxConvertedValue[]中存放的A/D采样的结果是DMA控制器在此之前存入的,它们被放置到即将进行FFT的浮点数组fft_buf_float[ ]的偶数地址中。而奇数地址中存放的是FFT输入的虚部,这里被全部置0。
1 //FFT函数的输入和输出都是复数,因此还有虚部,将输入填入实部,虚部为0 2 for(i = 0; i<256; i++){ 3 fft_buf_float[2*i] = uhADCxConvertedValue[i]; 4 fft_buf_float[2*i + 1] = 0; 5 }
3)由于STM32的ADC是单极性的(只有正数结果),其输入一定含有直流分量,其能量将远大于交流分量,影响FFT结果显示,因此在进行FFT之前先减去结果中的直流分量。(不去除直流分量的FFT结果,读者可以参见本博文后续实验结果部分所示)
1 //减去平均值,去除输入信号的直流成分(输入信号在浮点数组fft_buf_float[ ]的偶数地址中) 2 for(i = 0; i<256; i++) 3 sum = sum + fft_buf_float[2*i]; 4 average = sum/256; 5 for(i = 0; i<256; i++) 6 fft_buf_float[2*i] = fft_buf_float[2*i] - average;
4)对需要进行FFT计算的时域数据进行加窗
加窗的目的,是为了防止时域截断造成的能量泄露现象。(对不加窗数据进行FFT的结果,读者可以参见本博文后续实验结果部分所示)我使用了hanning窗,代码如下:
1 //加窗防止能量泄露 2 for(i = 0; i<256; i++) 3 fft_buf_float[2*i] = fft_buf_float[2*i] * hanning_win_table[i] ;
我没有在CMSIS-DSP库中找到窗函数,好在用Matlab计算浮点汉宁窗数值并不复杂,我将数组hanning_win_table[i]的数值罗列于此。

1 //256点汉宁窗 2 const float hanning_win_table[256] = 3 {0.000149421078453171, 0.000597595007177931, 0.00134425391964726, 0.00238895154954133, 0.00373106349747415, 0.00536978760418699, 0.00730414442998667, 0.00953297784014107, 0.0120549556958828, 0.0148685706506078, 0.0179721410507924, 0.0213638119410917, 0.0250415561730168, 0.0290031756165303, 0.0332463024738333, 0.0377684006945618, 0.0425667674915437, 0.0476385349562126, 0.0529806717727114, 0.0585899850296627, 0.0644631221285217, 0.0705965727873714, 0.0769866711389634, 0.0836295979217494, 0.0905213827625935, 0.0976579065498020, 0.105034903895052, 0.112647965682748, 0.120492541705279, 0.128563943382607, 0.136857346564560, 0.145367794414147, 0.154090200370186, 0.163019351187458, 0.172149910052584, 0.181476419773753, 0.190993306042403, 0.200694880764894, 0.210575345462196, 0.220628794735546, 0.230849219796014, 0.241230512055860, 0.251766466779543, 0.262450786792195, 0.273277086243339, 0.284238894423618, 0.295329659632231, 0.306542753092784, 0.317871472915207, 0.329309048101366, 0.340848642591985, 0.352483359352449, 0.364206244495054, 0.376010291435238, 0.387888445079305, 0.399833606041146, 0.411838634885427, 0.423896356394721, 0.435999563858022, 0.448141023378083, 0.460313478195001, 0.472509653023471, 0.484722258401111, 0.496943995045254, 0.509167558215622, 0.521385642080249, 0.533590944082063, 0.545776169303514, 0.557934034826625, 0.570057274085885, 0.582138641211355, 0.594170915359415, 0.606146905028547, 0.618059452357584, 0.629901437403849, 0.641665782398637, 0.653345455977481, 0.664933477382692, 0.676422920635650, 0.687806918676346, 0.699078667467724, 0.710231430062342, 0.721258540628942, 0.732153408436510, 0.742909521793458, 0.753520451939554, 0.763979856888295, 0.774281485217411, 0.784419179805244, 0.794386881510759, 0.804178632795004, 0.813788581281829, 0.823210983255770, 0.832440207094966, 0.841470736637101, 0.850297174476322, 0.858914245189185, 0.867316798487695, 0.875499812297549, 0.883458395759753, 0.891187792153812, 0.898683381740745, 0.905940684524234, 0.912955362928245, 0.919723224389528, 0.926240223863451, 0.932502466241655, 0.938506208680101, 0.944247862836110, 0.949723997013056, 0.954931338211443, 0.959866774085119, 0.964527354801480, 0.968910294804540, 0.973012974479810, 0.976832941720003, 0.980367913390621, 0.983615776694547, 0.986574590434830, 0.989242586174910, 0.991618169295584, 0.993699919948085, 0.995486593902703, 0.996977123292440, 0.998170617251262, 0.999066362446550, 0.999663823505453, 0.999962643334866, 0.999962643334866, 0.999663823505453, 0.999066362446550, 0.998170617251262, 0.996977123292440, 0.995486593902703, 0.993699919948085, 0.991618169295584, 0.989242586174910, 0.986574590434830, 0.983615776694547, 0.980367913390621, 0.976832941720003, 0.973012974479810, 0.968910294804540, 0.964527354801480, 0.959866774085119, 0.954931338211443, 0.949723997013056, 0.944247862836110, 0.938506208680101, 0.932502466241655, 0.926240223863451, 0.919723224389528, 0.912955362928245, 0.905940684524234, 0.898683381740745, 0.891187792153812, 0.883458395759753, 0.875499812297549, 0.867316798487695, 0.858914245189185, 0.850297174476322, 0.841470736637101, 0.832440207094966, 0.823210983255770, 0.813788581281829, 0.804178632795004, 0.794386881510759, 0.784419179805244, 0.774281485217411, 0.763979856888295, 0.753520451939554, 0.742909521793458, 0.732153408436510, 0.721258540628942, 0.710231430062342, 0.699078667467724, 0.687806918676346, 0.676422920635650, 0.664933477382692, 0.653345455977481, 0.641665782398637, 0.629901437403849, 0.618059452357584, 0.606146905028547, 0.594170915359415, 0.582138641211355, 0.570057274085885, 0.557934034826625, 0.545776169303514, 0.533590944082063, 0.521385642080249, 0.509167558215622, 0.496943995045254, 0.484722258401111, 0.472509653023471, 0.460313478195001, 0.448141023378083, 0.435999563858022, 0.423896356394721, 0.411838634885427, 0.399833606041146, 0.387888445079305, 0.376010291435238, 0.364206244495054, 0.352483359352449, 0.340848642591985, 0.329309048101366, 0.317871472915207, 0.306542753092784, 0.295329659632231, 0.284238894423618, 0.273277086243339, 0.262450786792195, 0.251766466779543, 0.241230512055860, 0.230849219796014, 0.220628794735546, 0.210575345462196, 0.200694880764894, 0.190993306042403, 0.181476419773753, 0.172149910052584, 0.163019351187458, 0.154090200370186, 0.145367794414147, 0.136857346564560, 0.128563943382607, 0.120492541705279, 0.112647965682748, 0.105034903895052, 0.0976579065498020, 0.0905213827625935, 0.0836295979217494, 0.0769866711389634, 0.0705965727873714, 0.0644631221285217, 0.0585899850296627, 0.0529806717727114, 0.0476385349562126, 0.0425667674915437, 0.0377684006945618, 0.0332463024738333, 0.0290031756165303, 0.0250415561730168, 0.0213638119410917, 0.0179721410507924, 0.0148685706506078, 0.0120549556958828, 0.00953297784014107, 0.00730414442998667, 0.00536978760418699, 0.00373106349747415, 0.00238895154954133, 0.00134425391964726, 0.000597595007177931, 0.000149421078453171 };
5)调用函数arm_cfft_f32();计算FFT结果
1 arm_cfft_f32(&arm_cfft_sR_f32_len256 , fft_buf_float , 0 , 1); 2 //FFT正变换,输出结果需要进行位翻转
其中第三个参数被置0,表示FFT算法是从时域向频域的正变换;第四个参数为1,表示需要对输出结果进行位翻转,以直接得到频率一次递增的频域数值。
6)将FFT结果转换为幅度谱
调用CMSIS-DSP库提供的函数arm_cmplx_mag_f32();计算信号的幅度谱(这将导致FFT结果中不同频率频谱的相位信息)。
1 arm_cmplx_mag_f32(fft_buf_float , fft_out_float , 256); 2 //FFT函数输出也是复数,这里只取了幅度
该函数的第一个参数指定了需要计算复数模的数组指针,第二个参数指定了计算结果存放的数组指针,第三个参数是需要计算复数模的数据个数。
7)将结果发送到PC进行显示
为更方便的观察和比较FFT结果,我使用以太网通过简单的UDP协议将数据上传到PC中显示。以下代码将结果存入缓冲区,其中float_un_buf是我事先定义的一个联合体,它由一个float数据和四个uchar数据构成。上述数据对象作为联合体成员,由于地址交叠,可以通过通过访问uchar数组将float数据转换为发送缓冲区所需的uchar类型。
1 //把浮点结果放到无符号字节型的发送缓冲当中 2 for(i = 0; i<256; i++) 3 { 4 float_un_buf.data_float = fft_out_float[i]; 5 Tx_Buffer[4*i] = float_un_buf.char_data[0]; 6 Tx_Buffer[4*i + 1] = float_un_buf.char_data[1]; 7 Tx_Buffer[4*i + 2] = float_un_buf.char_data[2]; 8 Tx_Buffer[4*i + 3] = float_un_buf.char_data[3]; 9 } 10 Write_SOCK_Data_Buffer(0, Tx_Buffer, 256*4);
四、实验结果
我使用STM32F4片上ADC(3.3V基准电压,采样率为1.4MSPS,DMA控制)对信号发生器产生的均值为1.65V,峰峰值为2V,频率202KHz的正弦信号进行了采样和FFT变换。然后将结果转换而成的幅度谱,通过UDP协议发送到PC上(接口芯片为W5500)。PC端程序开发平台为Visual Studio C# + NI Measurement studio。
1、观察频谱图(注意以下显示结果横轴数值不正确,由于是测试没有详细实现频域对应频率代码)
加汉宁窗并去除直流分量后显示结果如下图所示。
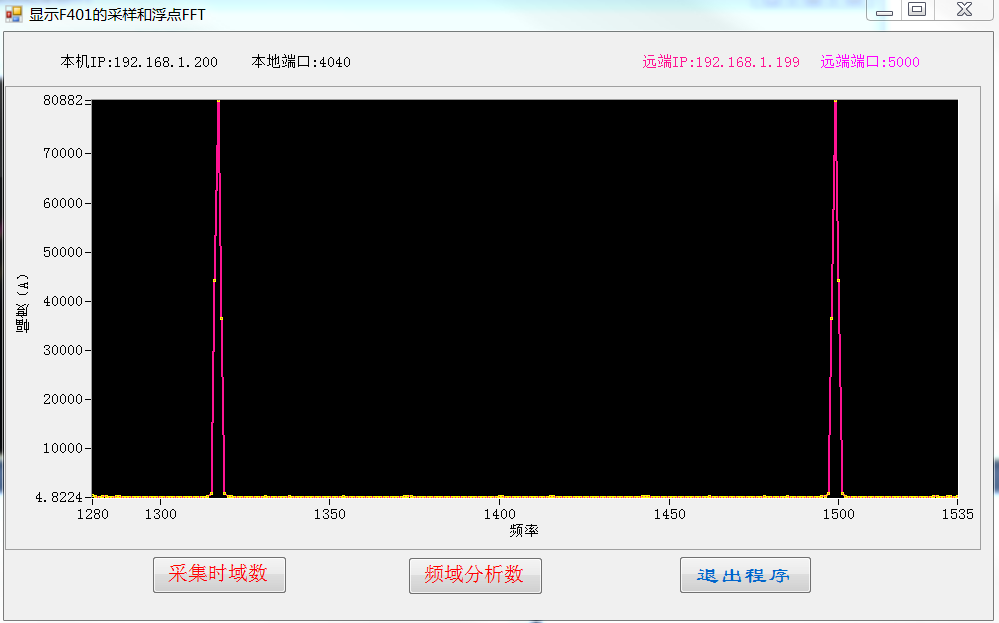
图4
不去除直流分量后显示结果如下图5所示。可以明显观察到加到的直流分量。
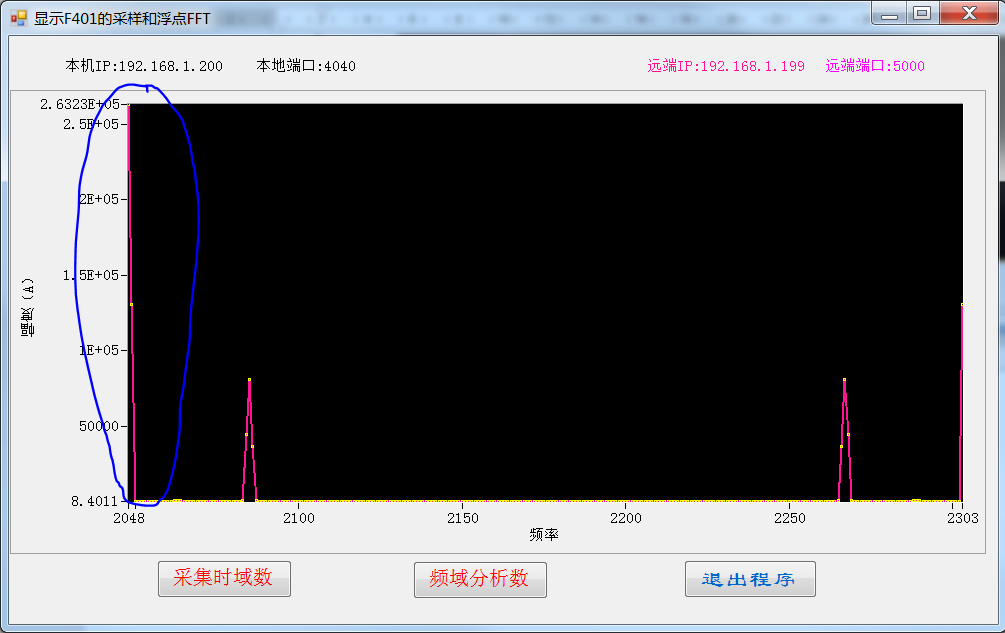
图5
不加汉宁窗结果如图6所示,可以观察到明显的能量泄露。
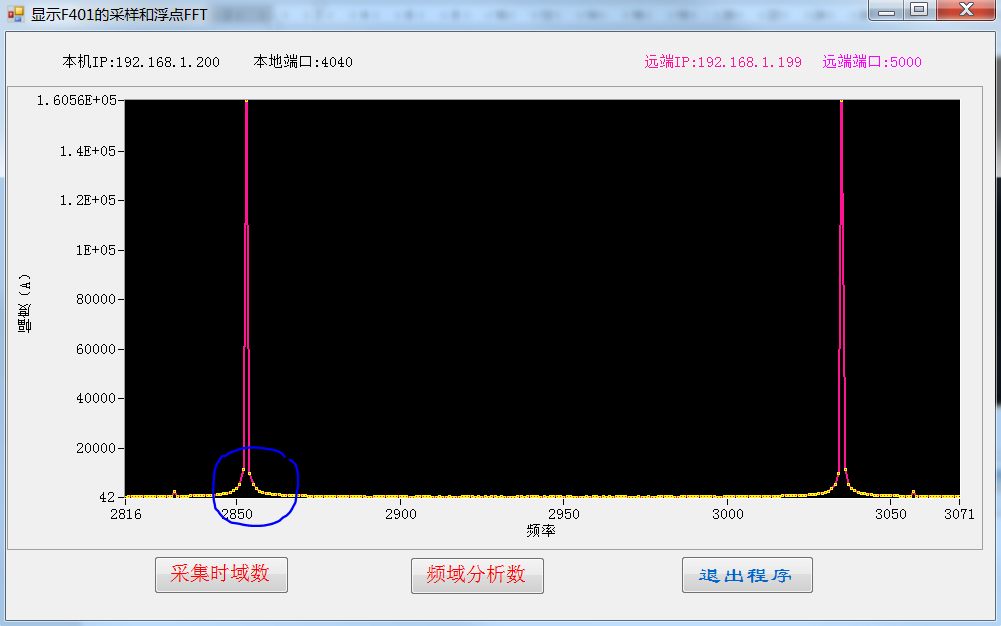
图6
若将输入改为锯齿波,如图7所示。可以明显的观察到几次谐波分量。
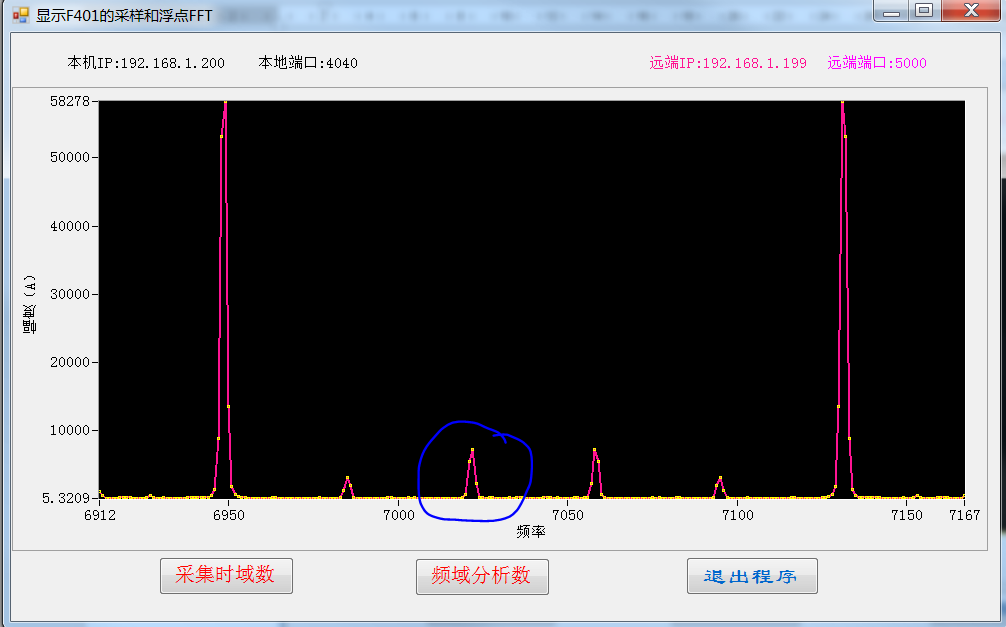
图7
2、STM32F40x浮点FFT转换时间性能
通过J-Link仿真器和Keil-MDK环境,对我使用的STM32F401RC@84MHz打开FPU和关闭FPU条件下256点的浮点FFT转换时间进行了测试,结果为——打开FPU:251.4us±5us;关闭FPU:4.9ms±100us
可见使用FPU后浮点FFT性能提高了约20倍。另外,读者如果想验证不使用FPU的算法时间,应将MDK工程中的库文件替代为arm_cortexM4l_math.lib,且options for target中的Floating Point Hardware选项(如图1所示)改为Not used。


![ARM DSP库CMSIS-DSP的使用——以STM32F4浮点FFT为例 [原创www.cnblogs.com/helesheng]](https://img2020.cnblogs.com/blog/1380455/202112/1380455-20211210184335734-2131974477.png) 本文介绍了使用STM32F4微控制器和ARM官方数字信号处理库(CMSIS DSP LIB)进行数字信号处理的基本操作和编程开发方法,并以快速傅里叶变换(FFT)为例,在MDK环境下,对STM32F4和CMSIS DSP LIB库的性能进行了评估。
本文介绍了使用STM32F4微控制器和ARM官方数字信号处理库(CMSIS DSP LIB)进行数字信号处理的基本操作和编程开发方法,并以快速傅里叶变换(FFT)为例,在MDK环境下,对STM32F4和CMSIS DSP LIB库的性能进行了评估。




【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 从 HTTP 原因短语缺失研究 HTTP/2 和 HTTP/3 的设计差异
· AI与.NET技术实操系列:向量存储与相似性搜索在 .NET 中的实现
· 基于Microsoft.Extensions.AI核心库实现RAG应用
· Linux系列:如何用heaptrack跟踪.NET程序的非托管内存泄露
· 开发者必知的日志记录最佳实践
· TypeScript + Deepseek 打造卜卦网站:技术与玄学的结合
· Manus的开源复刻OpenManus初探
· 写一个简单的SQL生成工具
· AI 智能体引爆开源社区「GitHub 热点速览」
· C#/.NET/.NET Core技术前沿周刊 | 第 29 期(2025年3.1-3.9)