关于数组为什么要1.5倍或者2倍扩容
一、为什么不是常数扩容而是成倍扩容
首先我们要明确数组是一块连续的内存，在添加元素的过程中，如果我们的数组存不下了，则需要开辟一块新的内存，把原来的元素复制到新开辟的地方，具体过程如下：
- 新开辟(allocate)足够大小的内存
- 把旧元素复制到新的内存中
- 释放(deallocate)原来的内存
其中第二步需要的时间复杂度为O(n)，这样我们有一个时间和空间的tradeoff，就是说如果我们新开辟的内存很大，一次开辟可以存很多新元素进去，我们reallocation、复制的次数会少，但是很可能会浪费很多空间；如果每次新开辟只比原来的内存大一点，空间浪费很少，不过reallocation、复制的次数会很多。
下面我们比较一下常数扩容和成倍扩容的时间复杂度：
1. 选择常数扩容，即每次扩容的空间比原来大c
假如说初始数组有1个元素，每次扩容空间增加1，最终扩容成容纳n个元素，则每次扩容，复制旧元素和加入新元素，添加元素(append)的次数如下：
扩容次数 数组长度 append次数
0 1 1 （复制0个，新加入1个）
1 2 2 （复制1个，新加入1个）
2 3 3 （复制2个，新加入1个）
... ... ...
n-1 n n
共计 1 + 2 + 3 + ... + n = \(O(n^2)\)，均摊到每个元素则是\(O(n)\)。（或者可以这样理解，到最后n个元素中，第一个元素（最老的元素）被append了n次，第二个元素被append了n-1次，以此类推，最后一个元素被append了1次）
扩容c个只有字母前面倍数的差别，均摊还是\(O(n)\)
2. 选择成倍扩容
每次扩容2倍，最终扩容成容纳n个元素，则复制的次数如图：
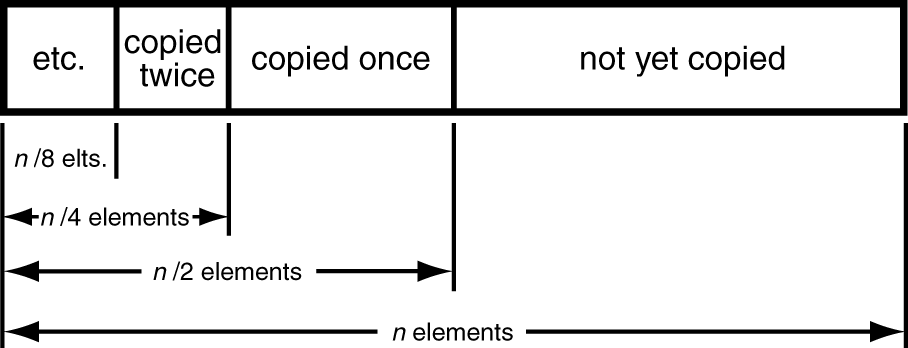
图中是被copy的次数，我们这里算被append的次数（被copy的次数加1）：
最终数组里的n个元素中，n个元素append次数至少是1，n/2个元素append次数至少是2，n/4个元素append次数至少是3，以此类推，则共计 n + n/2 + n/4 + n/8 + ... = \(O(n)\)，均摊到每个元素是\(O(1)\)
（解释一下这个式子，以第二项为例，n/2个元素是包含在n个元素里的，这n/2个元素的1次append已经在第一项里算过一遍了，所以每一项不用乘被append次数）
常数扩容均摊的时间复杂度为\(O(n)\)，根据时间复杂度的比较，我们选择成倍扩容
二、为什么选择2倍扩容或1.5倍扩容？
不选择更大倍数的扩容是为了避免浪费更多空间
选择1.5倍扩容还有一个好处，就是可以使用前面释放的空间，如图所示：
第一部分来自 https://www.drdobbs.com/c-made-easier-how-vectors-grow/184401375 解释了为什么不用常数扩容
第二部分来自 https://blog.csdn.net/qq_44918090/article/details/120583540 面试题：C++vector的动态扩容，为何是1.5倍或者是2倍
第二个链接关于扩容问题写的很全面
