DS博客作业02--栈和队列
0. PTA得分截图

1. 本周学习总结
1.1 总结栈和队列内容
1.1.1 栈
- 栈的定义
栈是一种只能在一端进行插入或删除的线性表,主要特点是先进后出
栈的几个概念
允许进行插入、删除操作的一端称为栈顶。
表的另一端称为栈底。
当栈中没有数据元素时,称为空栈。
栈的插入操作通常称为进栈或入栈。
栈的删除操作通常称为退栈或出栈。
- 顺序栈
假设栈的元素个数最大不超过正整数MaxSize,所有的元素都具有同一数据类型ElemType,则可用下列方式来定义顺序栈类型SqStack:
typedef struct
{ ElemType data[MaxSize];
int top;//栈顶指针
} SqStack;
假设MaxSize=5
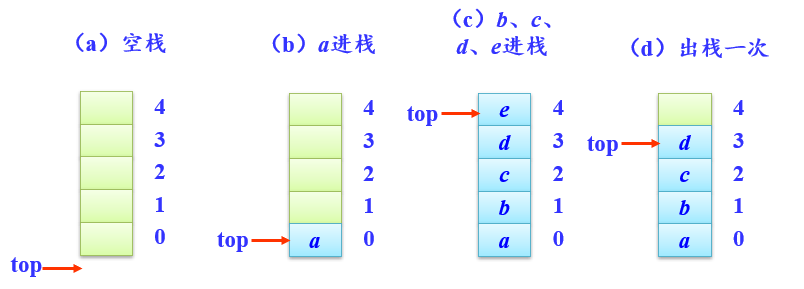
top指向栈顶元素,初始值为-1
当top=MaxSize-1时不能再进栈——即栈满
进栈时top+1,出栈时top-1
顺序栈4要素
栈空条件:top=-1
栈满条件:top=MaxSize-1
e进栈操作:top++;将e放在top处;
e出栈操作:从top处取出元素e;top--;栈内元素没有被删除
- 顺序栈的基本运算算法
初始化栈
- 建立一个新的空栈s,实际上是将栈顶指针指向-1即可
具体代码示例
void InitStack(SqStack &s)
{
s=new Stack;
s->top=-1;
}
销毁栈
- 释放栈s占用的存储空间
具体代码示例
void DestroyStack(SqStack &s)
{
delete s;
}
判断栈是否为空
- 栈为空的条件是s->top=-1
具体代码示例
bool StackEmpty(SqStack s)
{
return(s->top==-1);
}
进栈
- 在栈不满的条件下,先将栈指针+1,然后在该位置上插入元素e 一定要考虑栈满的情况!
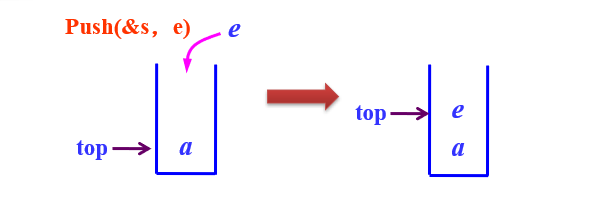
具体代码示例
bool Push(SqStack &s,ElemType e)
{
if (s->top==MaxSize-1) //栈满的情况,即栈上溢出
return false;
s->top++; //栈顶指针增1
s->data[s->top]=e; //元素e放在栈顶指针的地方
return true;
}
出栈
- 在栈不空的情况下,先将栈顶元素赋给e,然后将栈顶指针-1
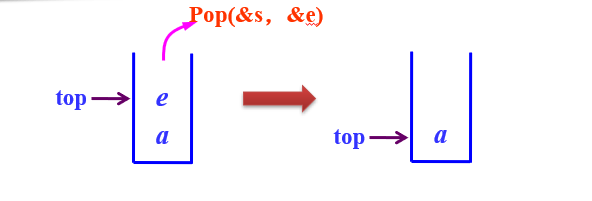
具体代码示例
bool Pop(SqStack &s,ElemType &e)
{
if (s->top==-1) //栈为空的情况,即栈下溢出
return false;
e=s->data[s->top]; //取栈顶指针元素
s->top--; //栈顶指针减1
return true;
}
取栈顶元素
- 在栈不空的情况下,将栈顶元素赋给e
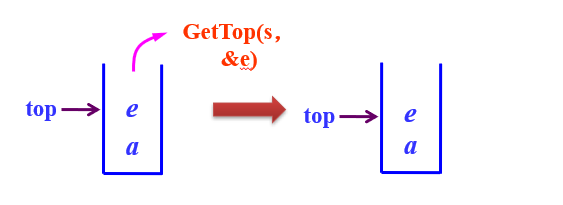
具体代码示例
bool GetTop(SqStack s,ElemType &e)
{
if (s->top==-1) //栈为空的情况,即栈下溢出
return false;
e=s->data[s->top]; //取栈顶指针元素的元素
return true;
}
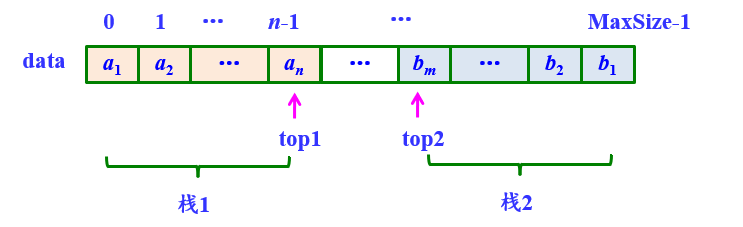
- 共享栈
如果需要用到两个相同类型的栈,可以用一个数组data[0..MaxSize-1来实现这两个栈,这称为共享栈。
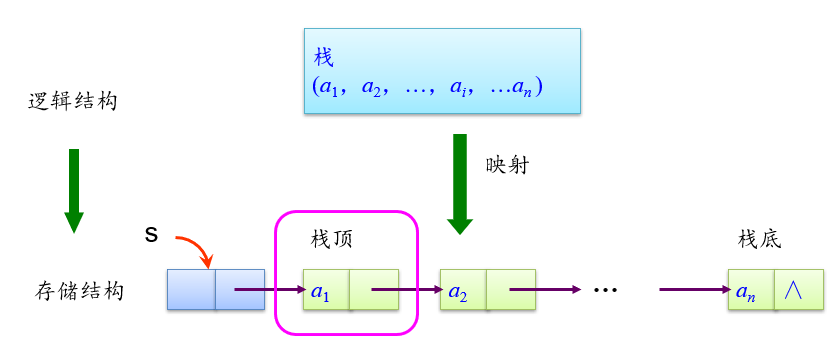
- 链栈
链栈中数据节点的类型LiStack定义如下:
typedef int ElemType;
typedef struct linknode
{ ElemType data; //数据域
struct linknode *next; //指针域
} LiNode,*LiStack;
链栈4要素
栈空条件:s->next=NULL
栈满条件:不考虑
进栈e操作:结点插入到头结点后,链表头插法
退栈操作:取出头结点之后结点的元素并删除
- 链栈的基本运算算法
初始化栈
void InitStack(LiStack &s)
{
s=new LiNode;
s->next=NULL;
}
销毁栈
- 释放栈s占用的全部存储空间,这里栈内元素是被删除的了
void DestroyStack(LiStack &s)
{
LiStack p;
while (s!=NULL)
{
p=s;
s=s->next;
free(p);
}
}
取栈顶元素
- 同样要在栈不为空的条件下操作
bool GetTop(LiStack s,ElemType &e)
{
if (s->next==NULL) //栈空的情况
return false;
e=s->next->data;
return true;
}
判断栈是否为空
- 栈为空的条件是s->next==NULL
bool StackEmpty(LiStack s)
{
return(s->next==NULL);
}
进栈
- 链栈与顺序栈不同,不需要考虑栈满的情况
void Push(LiStack &s,ElemType e)
{
LiStack p;
p=new LiNode;
p->data=e; //新建元素e对应的节点p
p->next=s->next; //插入p节点作为开始节点
s->next=p;
}
出栈
- 与顺序栈相同,也要考虑栈空的情况,不过链栈是将栈内数据物理删除,而顺序栈并没有删除栈内元素
bool Pop(LiStack &s,ElemType &e)
{
LiStack p;
if (s->next==NULL) //栈空的情况
return false;
p=s->next;
e=p->data;
s->next=p->next;
free(p); //释放p节点
return true;
}
- c++模板类:stack
#include<stack>头文件1.stack
s:初始化栈,参数表示元素类型 2.s.push(t):入栈元素t
3.s.top():返回栈顶元素
4.s.pop():出栈操作只是删除栈顶元素,并不返回该元素 物理删除,数据在栈内不存在
5.s1.empty():当栈空时,返回true
6.s1.size():访问栈中的元素个数
- 栈的应用
1.输入之后逆序输出
2.语法检查:括号匹配
每当扫描到大中小的括号后,令其进栈,当扫描到右括号时,则检查栈顶是否为相应的左括号,若是,则出栈处理,若不是,则出现了语法错误。当扫描到文件结尾,若栈为空则表明没有发现括号配对错误。
3.数制转换
十进制转八进制。例如(1348)十进制= (2504)八进制,N不断的除8,每次的余数就是结果的其中一个因子,注意先出来的因子是低位的数,可以考虑用栈来保存每次取余的结果,那么出栈的顺序就是实际的结果顺序。
| N | N/8 | N%8 |
|---|---|---|
| 1348 | 168 | 4 |
| 168 | 21 | 0 |
| 21 | 2 | 5 |
| 2 | 0 | 2 |
4.中缀和后缀表达式的转换及计算
1.中缀表达式转换成后缀表达式的转化思路
从头到尾扫描中缀表达式,若遇到数字则直接写入后缀表达式,若遇到运算符,则比较栈顶元素和该运算符的优先级,当该运算符的优先级大于栈顶元素的时候,表明该运算符的后一个运算对象还没有进入后缀表达式,应该把该运算符暂存于运算符栈中,然后把它的后一个运算对象写入到后缀表达式中,再令其出栈并写入后缀表达式中;若遇到的运算符优先级小于等于栈顶元素的优先级,表明栈顶运算符的两个运算对象已经被写入后缀表达式,应将栈顶元素出栈并写入后缀表达式,对于新的栈顶元素仍进行比较和处理,直到栈顶元素的优先级小于当前等待处理的运算符的优先级为止,然后令该运算符进栈即可。
对于左括号直接进栈,右括号则使左右两个括号内的运算符都出栈
2.后缀表达式求值
后缀表达式求值也需要一个栈,其元素类型为操作数的类型,此栈存储后缀表达式中的操作数、计算过程的中间结果及最后结果。
计算过程:扫描后缀表达式,若遇到操作数则进栈,若遇到操作符则弹出两个操作数进行计算,然后将结果压进栈,直到最后扫描完毕,栈中应该保存着最终结果。
1.1.2 队列
- 队列的定义

队列只能选取一个端点进行插入操作,另一个端点进行删除操作
队列的主要特点是先进先出
队列的几个概念
把进行插入的一端称做队尾(rear)
进行删除的一端称做队首或队头(front)
向队列中插入新元素称为进队或入队,新元素进队后就成为新的队尾元素
从队列中删除元素称为出队或离队,元素出队后,其后继元素就成为队首元素
- 顺序队
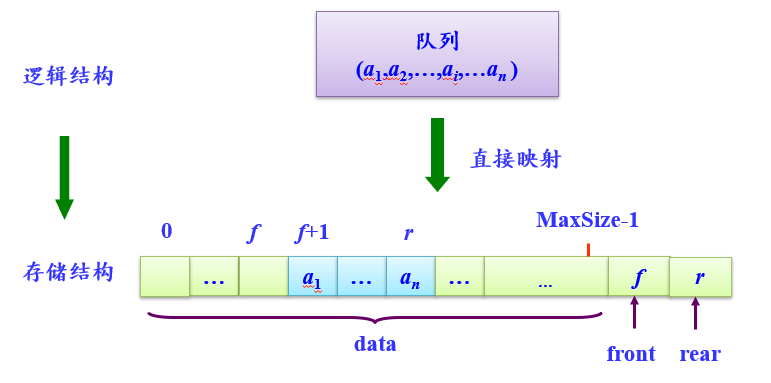
定义顺序队:
typedef struct
{
ElemType data[MaxSize];
int front,rear;//队首和队尾指针
}SqQueue;
因为队列的两端都在变化,所以需要两个指针来表示队列的状态
假设MaxSize=5
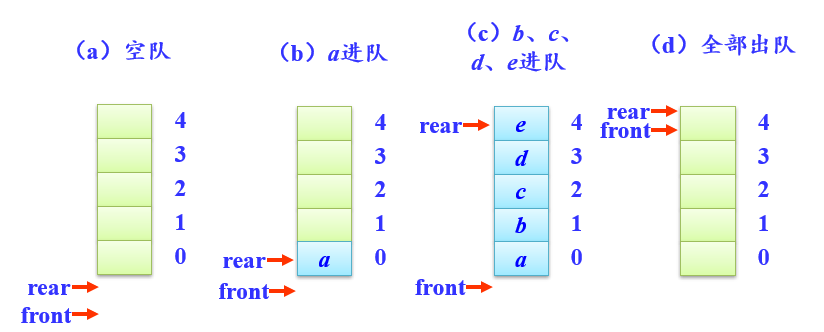
rear总是指向队尾元素
元素进队时,rear+1
front指向当前队中队头元素的前一个位置
元素出队时,front+1
当rear=MaxSize-1时不能再进队
- 队列的基本运算
初始化队列
- 构造一个空队列q,将front和rear指针均设置成初始状态即-1
void InitQueue(SqQueue *&q)
{
q=new SqQueue;
q->front=q->rear=-1;
}
销毁队列
void DestroyQueue(SqQueue *&q)
{
free(q);
}
判断队列是否为空
- 当q->front==q->rear时队列为空
bool QueueEmpty(SqQueue *q)
{
return(q->front==q->rear);
}
进队列
- 在队列不满的条件下,先将队尾指针rear循环增1,然后将元素添加到该位置
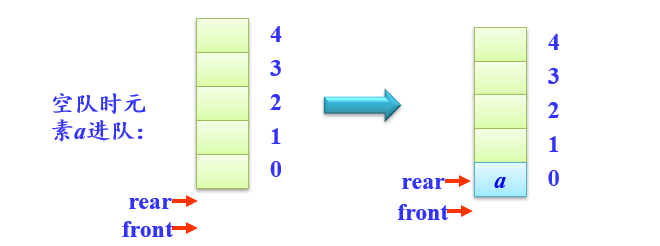
bool enQueue(SqQueue *&q,ElemType e)
{
if (q->rear==MaxSize-1) //队满上溢出
return false;
q->rear++;
q->data[q->rear]=e;
return true;
}
出队列
- 在队列q不为空的条件下,将队首指针front循环增1,并将该位置的元素值赋给e
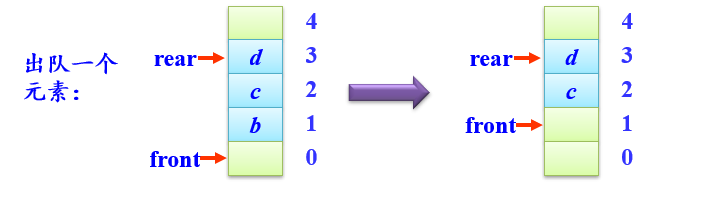
bool deQueue(SqQueue *&q,ElemType &e)
{
if (q->front==q->rear) //队空下溢出
return false;
q->front++;
e=q->data[q->front];
return true;
}
- 循环队列
当采用rear==MaxSize-1作为队满条件时,当其为真,队中可能还有若干空位置,这种溢出并不是真正的溢出,称为假溢出。
解决假溢出的问题,就需要把数组的前端和后端连接起来,形成一个环形的顺序表,即把存储队列元素的表从逻辑上看成一个环,称为环形队列或循环队列。
for example
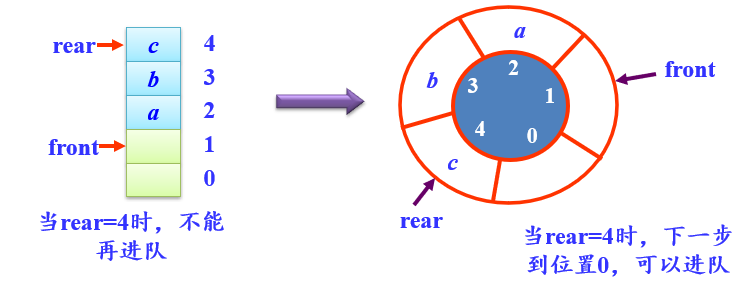
环形队列4要素
队空条件:front==rear
队满条件:(rear+1)%MaxSize==front
e进队操作:rear=(rear+1)%MaxSize //将e放在rear处
e出队操作:front=(front+1)%MaxSize //取出front处的元素e
已知front、rear,求count?
count=(rear-front+MaxSize)%MaxSize
已知front、count,求rear?
rear=(front+count)%MaxSize
已知rear、count,求front?
front=(rear-count+MaxSize)%MaxSize
- 链队列
优点
1.相比普通的队列,元素出队时无需移动大量元素,只需移动头指针。
2.可动态分配空间,不需要预先分配大量存储空间。
3.适合处理用户排队等待的情况。
入队
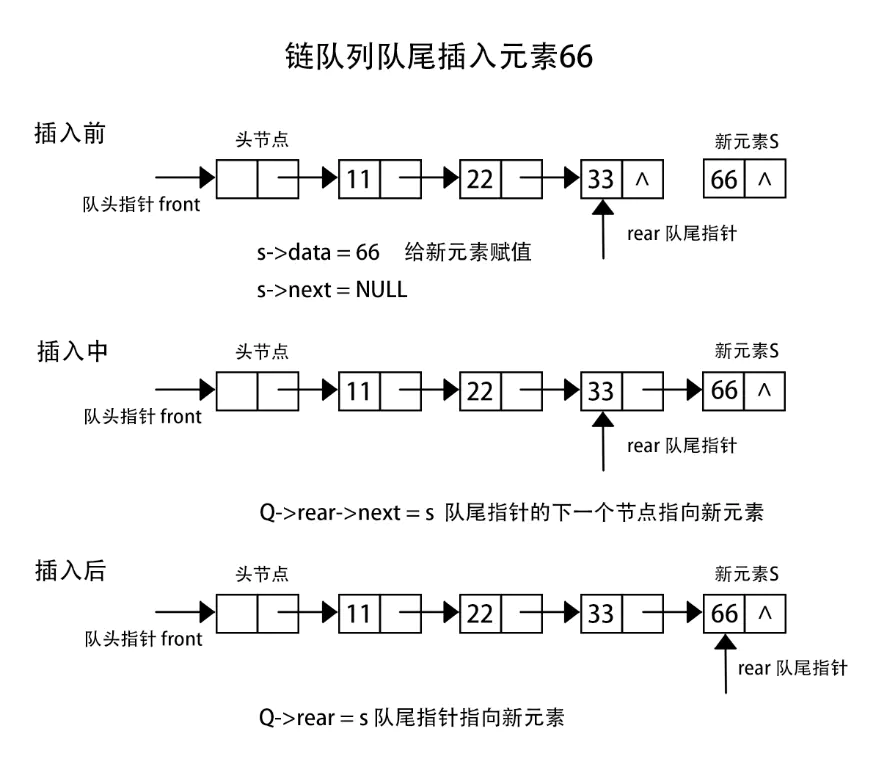
Status EnQueue(LinkQueue *Q, ElemType e)
{
// 给新节点分配空间
QueuePtr s =new QNode;
// 分配空间失败,结束程序
if (!s)
{
exit(OVERFLOW);
}
s->data = e; // 将值赋值给新节点
s->next = NULL; // 新节点指向NULL
Q->rear->next = s; // 队尾指针的下一个元素指向新节点
Q->rear = s; // 队尾指针指向新节点(新节点成为队尾指针的指向的节点)
return OK;
}
出队
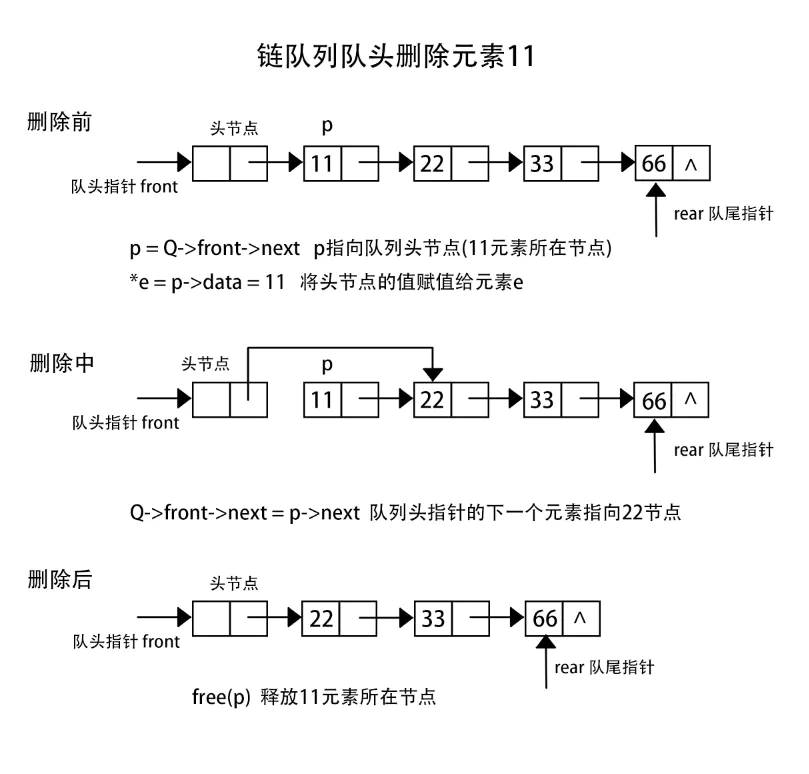
Status DeQueue(LinkQueue *Q, ElemType *e)
{
QueuePtr p; // 用于指向被删除节点
// 队列为空,出队失败
if (Q->front == Q->rear)
{
return ERROR;
}
p = Q->front->next; // p指向队列的第一个元素
*e = p->data; // 将队列头节点的值赋值给元素e
Q->front->next = p->next; // 头指针的下一个节点指向下下个节点(跳过头节点)
// 如果被删除节点是队尾指针指向的节点(删除后队列为空)
if (Q->rear == p)
{
Q->rear = Q->front; // 队尾指针指向队头指针
}
free(p); // 释放队头节点
return OK;
}
- c++容器:queue
#include<queue>q1.push(x):将x接到队列的末端
q1.pop():弹出队列的第一个元素 并不会返回被弹出元素的值,要先取队头再pop
q1.front():即最先被压入栈中的元素
q1.back():即最后被压入栈中的元素
q1.empty():当队列为空时返回true
q1.size():访问队列中的元素个数
- 队列的应用
1.输入之后正序输出
2.迷宫寻找最短路径
因为队列是深度优先搜索,可以比栈更快的找出最短路径
3.排队问题
比如售票机取票先排到的人就先取票 or 银行三兄弟经典问题 😄
1.1.3 栈与队列的异同
相同点
- 都是线性结构
- 插入操作都是在表尾进行
- 插入和删除的时间复杂度都是O(1),在空间复杂度上也相同
- 都可以通过顺序结构和链表实现
不同点
- 删除数据元素的位置不同,栈在表尾进行,队列在表头进行
- 顺序栈能够实现多栈空间共享,而顺序队列不能
- 应用场景不同;常见栈的应用场景包括括号问题的求解,表达式的转换和求值,函数调用和递归实现,深度优先搜索遍历等;常见的队列的应用场景包括银行排队和广度优先搜索遍历等
1.2 谈谈你对栈和队列的认识及学习体会
栈和队列从概念上相对比较好理解。一开始学习是通过数组的方式存储数据。接着后学习了用链表的方式存储数据。我们可以通过栈或队列,完成表达式转换,符号配对,迷宫等需要存储后在逆序或正序输出的程序功能。
目前接触到了c++容器stack(栈)和queue(队列),这两种模板很实用,但第一次使用还是容易出错:在调用模板的函数时没有加括号,如要对栈s调用pop函数,写成了s.pop,导致程序崩溃
还有就是在写程序的过程中要时刻记得判断是否为空,否则程序也会报错(自己写程序就容易忘记 害
2. PTA实验作业
2.1 报数游戏
报数游戏是这样的:有n个人围成一圈,按顺序从1到n编好号。从第一个人开始报数,报到m(m<n)的人退出圈子;下一个人从1开始报数,报到m的人退出圈子。如此下去,直到留下最后一个人。其中n是初始人数;m是游戏规定的退出位次(保证为小于n的正整数)。要求用队列结构完成。输出数字间以空格分隔,但结尾不能有多余空格。
2.1.1 代码截图
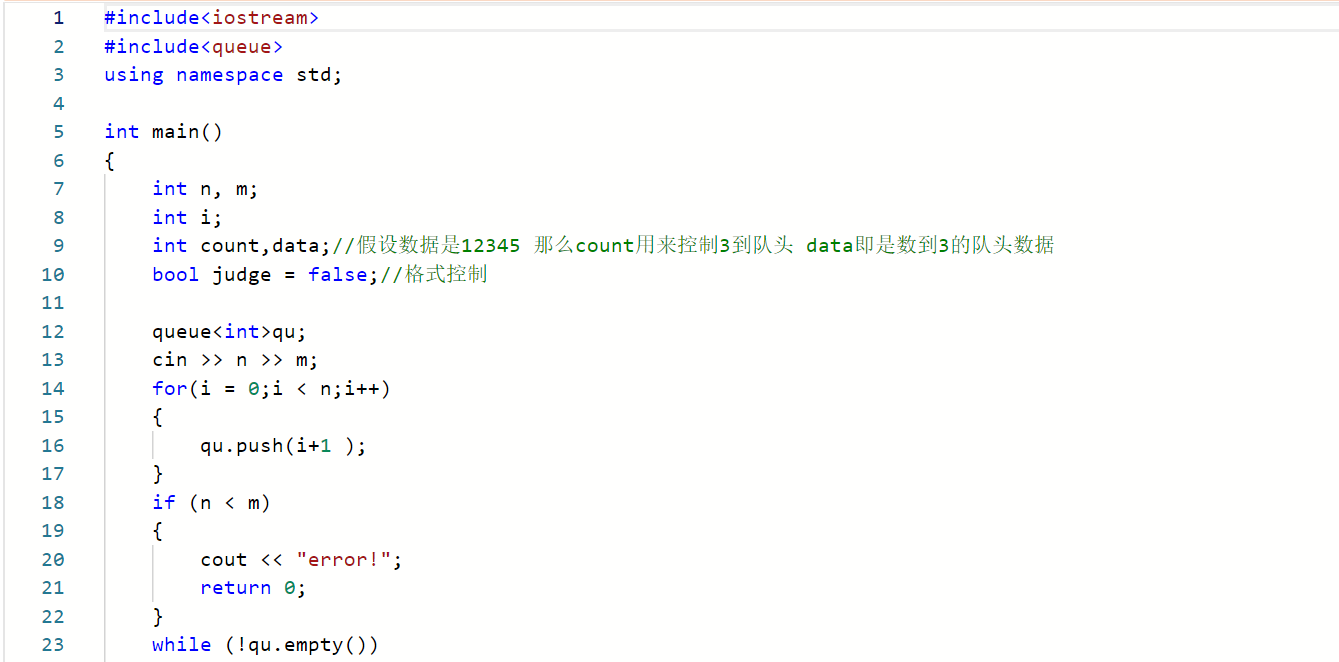
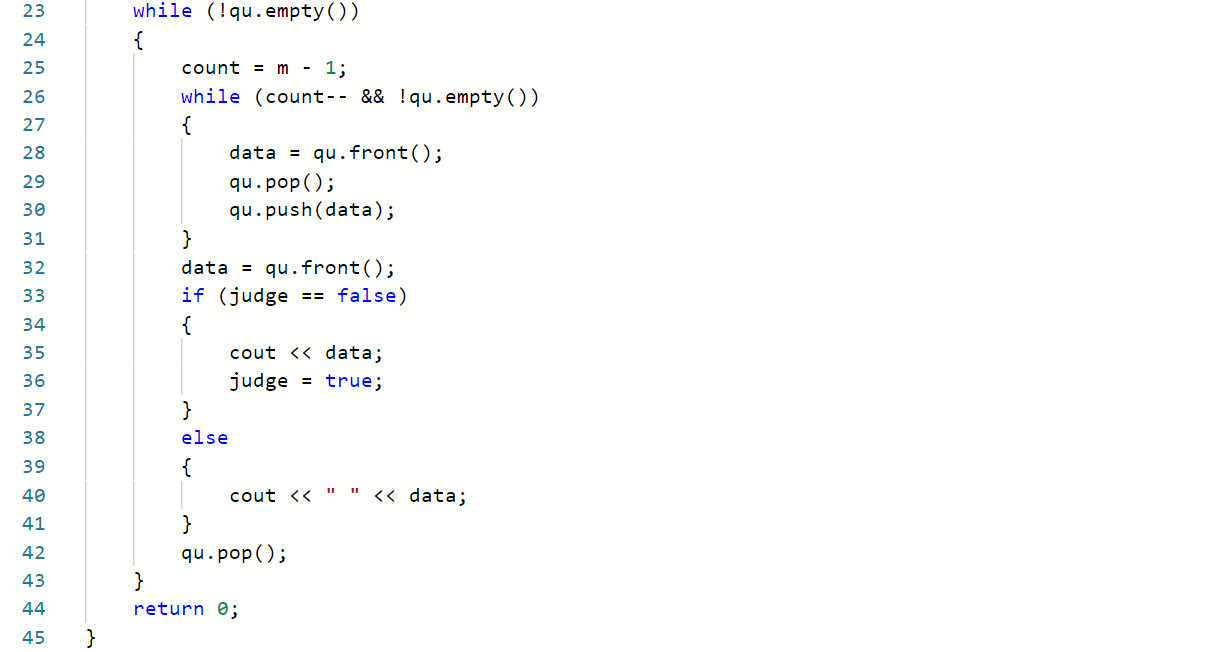
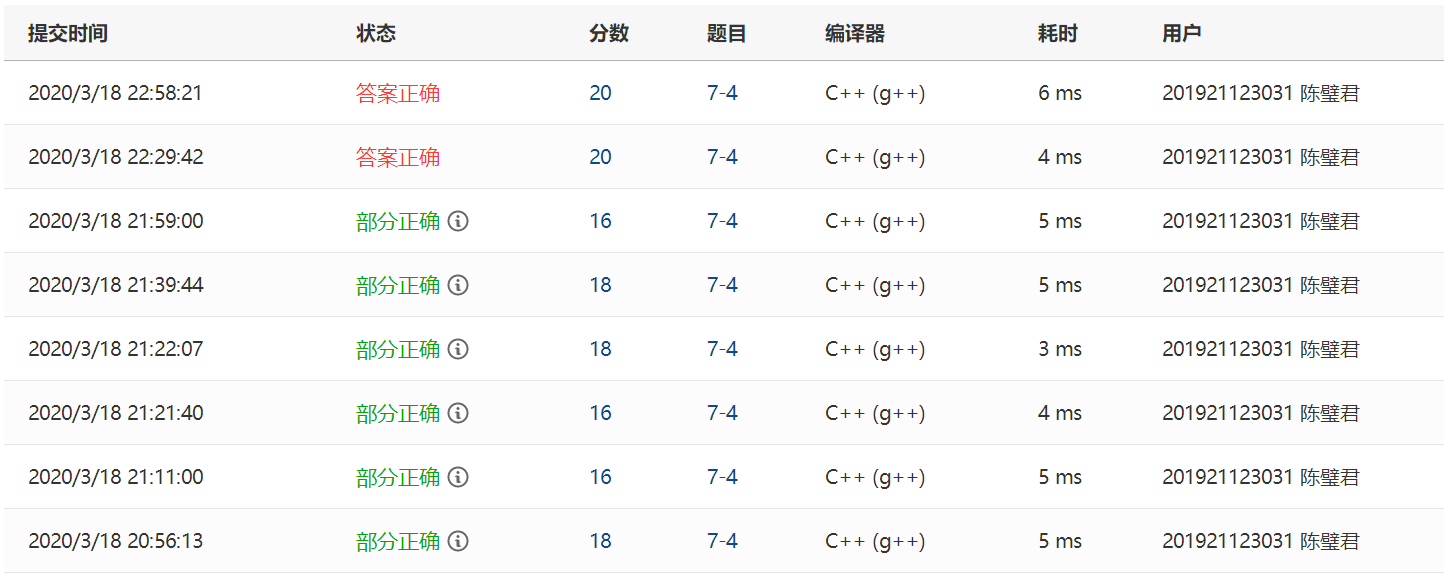
2.1.2 本题PTA提交列表说明
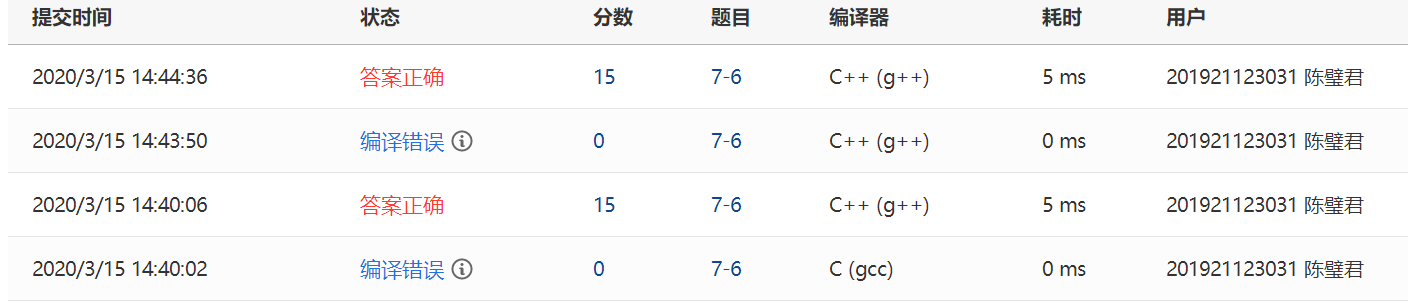
第一个编译错误是因为没有转换c++的编译器
第二个编译错误是因为在看代码的时候发现忘记加return 0了 结果在敲的时候把分号用中文输入法输入就错了
还有一个是在vs编译中,我一开始将编号入队的时候是用push(i),结果输出的数字都跟答案差1,然后经过调试发现应该要push(i+1)
2.2 符号配对
请编写程序检查C语言源程序中下列符号是否配对:
/*与*/、(与)、[与]、{与}
2.2.1 代码截图
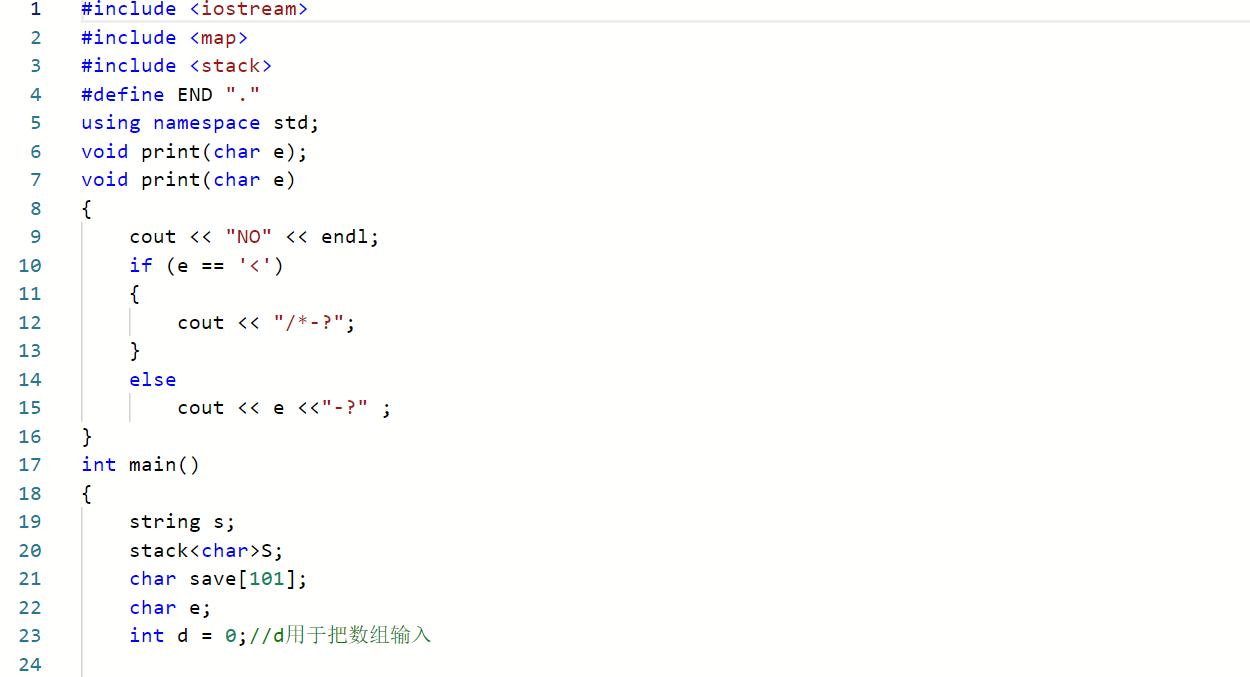

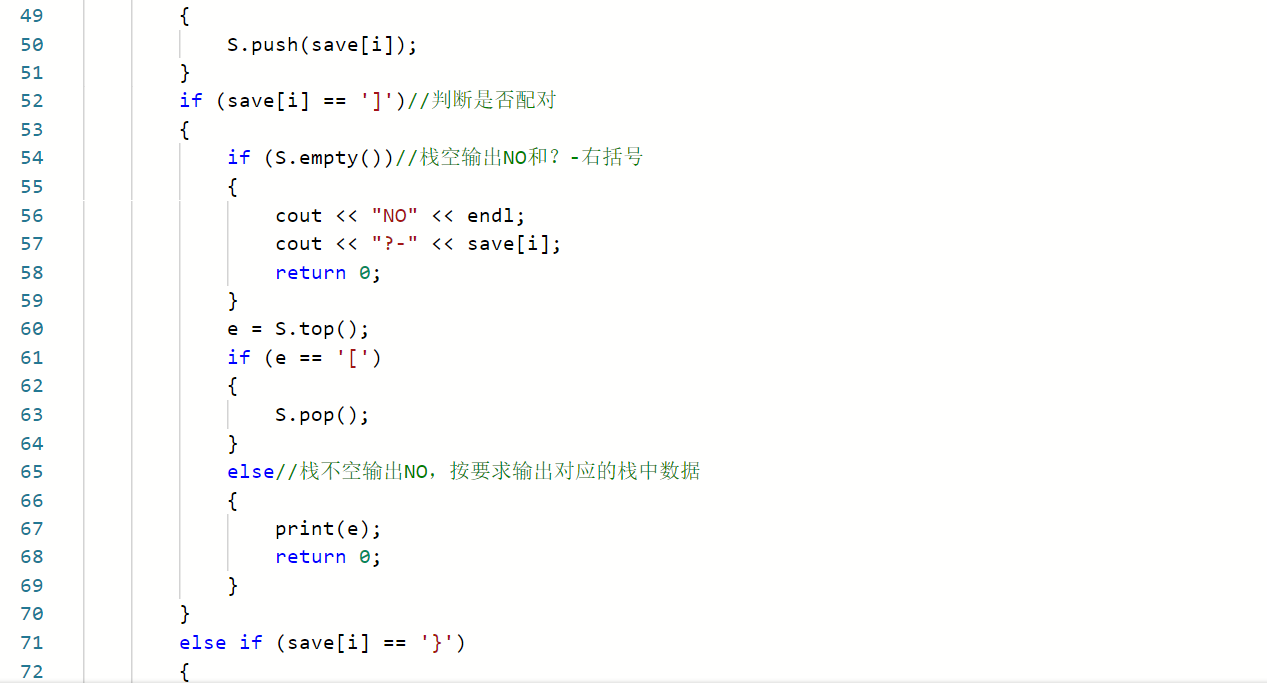



2.2.2 本题PTA提交列表说明
我觉得这道浙大的符号配对跟7-3比起来难度提升了不少,一开始是没什么头绪,没明白题目的意思。第一个不配对的字符我一开始以为是从左往右数的第一个,就一直搞不懂怎么判断。后来是参考CSDN的代码,才知道是从中间往两边数的第一个不配对字符。
在参考代码的同时我也学会了用
<>来代替/**/,这样的做法会比直接判断注释符是否配对来的简单耶然后提交了好几次代码,最后一个测试点老是过不了,也不太理解最后一个测试点的意思。
我一开始是以为我的数组太小了,但是后来改大了之后也还是过不了。问了同学之后才知道是我没有把第一个不配对的字符及时pop出去。
3. 阅读代码
3.1 题目及解题代码
-
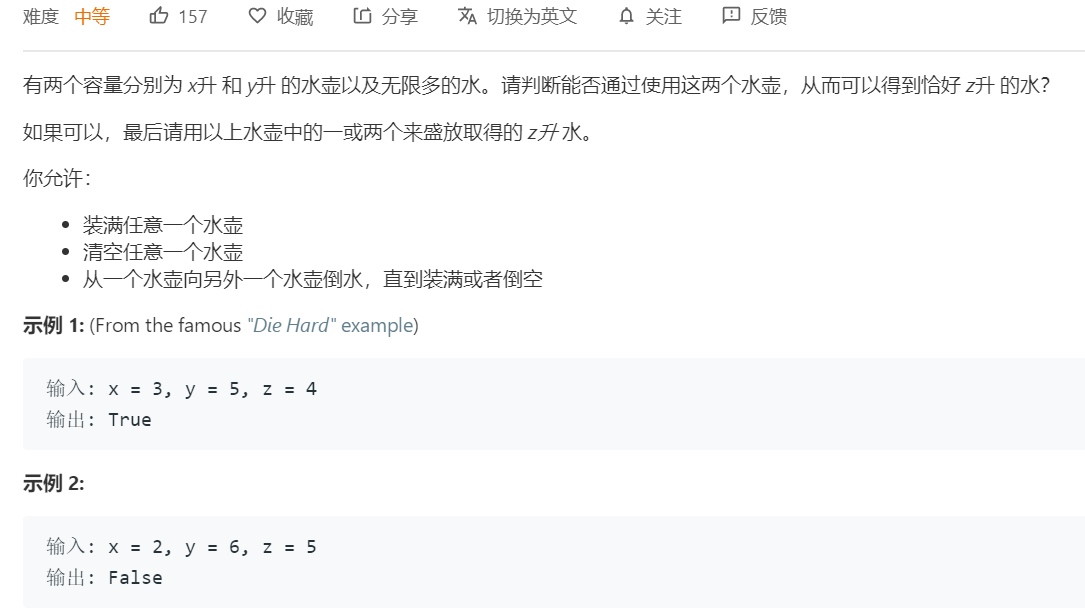
题目:
-
代码:
class Solution {
public:
bool canMeasureWater(int x, int y, int z) {
if (x + y < z) return false;
if (x == 0 || y == 0) return z == 0 || x + y == z;
return z % gcd(x, y) == 0;
}
};
3.1.1 设计思路
-
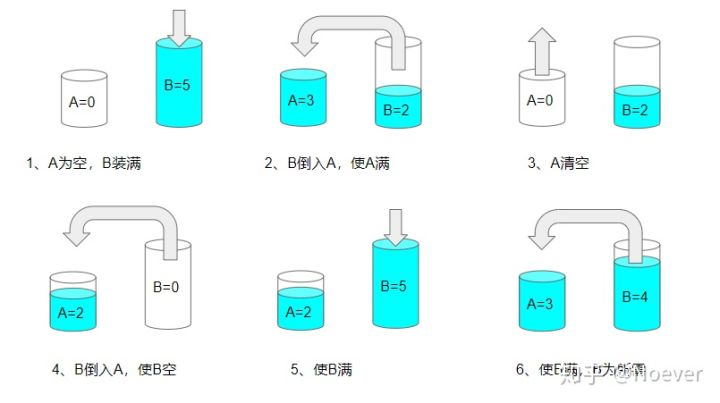
对于示例1的理解:
-
思路及算法
预备知识:贝祖定理
我们认为,每次操作只会让桶里的水总量增加 x,增加 y,减少 x,或者减少 y。
因此,我们可以认为每次操作只会给水的总量带来 x 或者 y 的变化量。因此我们的目标可以改写成:找到一对整数a,b,使得ax+by=z
而只要满足z≤x+y,且这样的a,b 存在,那么我们的目标就是可以达成的。这是因为:
若a≥0,b≥0,那么显然可以达成目标。
若a<0,那么可以进行以下操作:
往 y 壶倒水;
把 y 壶的水倒入 x 壶;
如果 y 壶不为空,那么 x 壶肯定是满的,把 x 壶倒空,然后再把 y 壶的水倒入 x 壶。
重复以上操作直至某一步时 x 壶进行了 a 次倒空操作,y 壶进行了 b 次倒水操作。
若b<0,方法同上,x 与 y 互换。
而贝祖定理告诉我们,ax+by=z 有解当且仅当 z 是 x,y 的最大公约数的倍数。因此我们只需要找到 x,y 的最大公约数并判断 z 是否是它的倍数即可。
时间复杂度:O(log(min(x,y)))
空间复杂度:O(1)
3.1.2 伪代码
if(所需要z的水量大于x+y的水壶可以盛水的总量)return false;
if(x或y为0) return z==0||x+y==z;
if(z是x、y最大公约数的倍数) return true;
else return false;
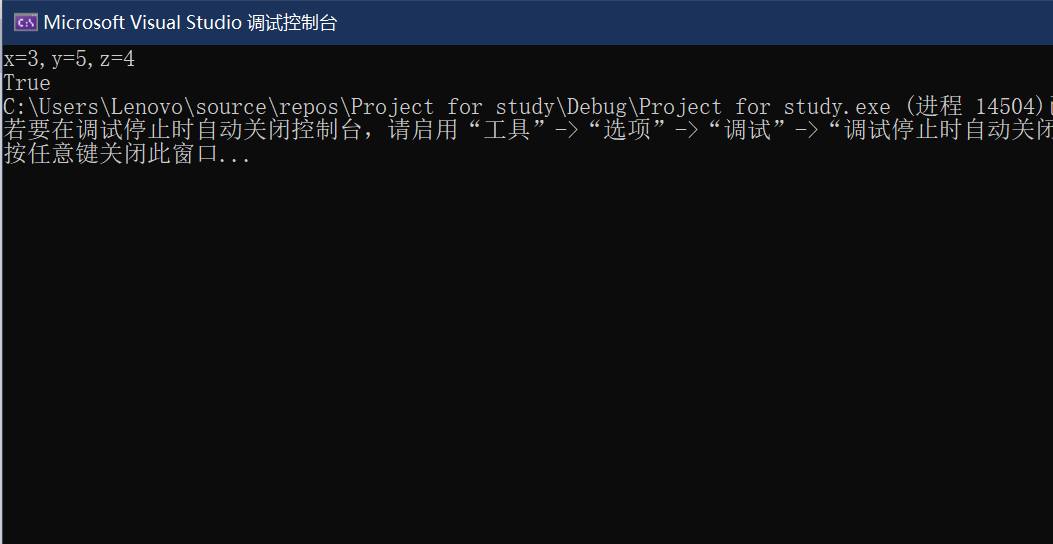
3.1.3 运行结果
3.1.4 分析该题目解题优势及难点
优点
1.这题运用数学原理来解题真的超快,一开始看题目连题目都没太看懂,然后看了官方解答,震惊于怎么会有这么机智的解法
2.与单纯的c++解法相比,时间复杂度和空间复杂度都小了很多
难点
1.这个数学原理虽然真的把代码简化了非常多,但是吧,对于没有了解过这个原理的人(比如我)来说,是真的难搞,数学思想真的有一定难度
3.2 题目及解题代码
-
题目:

-
代码:
class Solution {
public:
vector<vector<int>> reconstructQueue(vector<vector<int>>& people) {
// 先排序
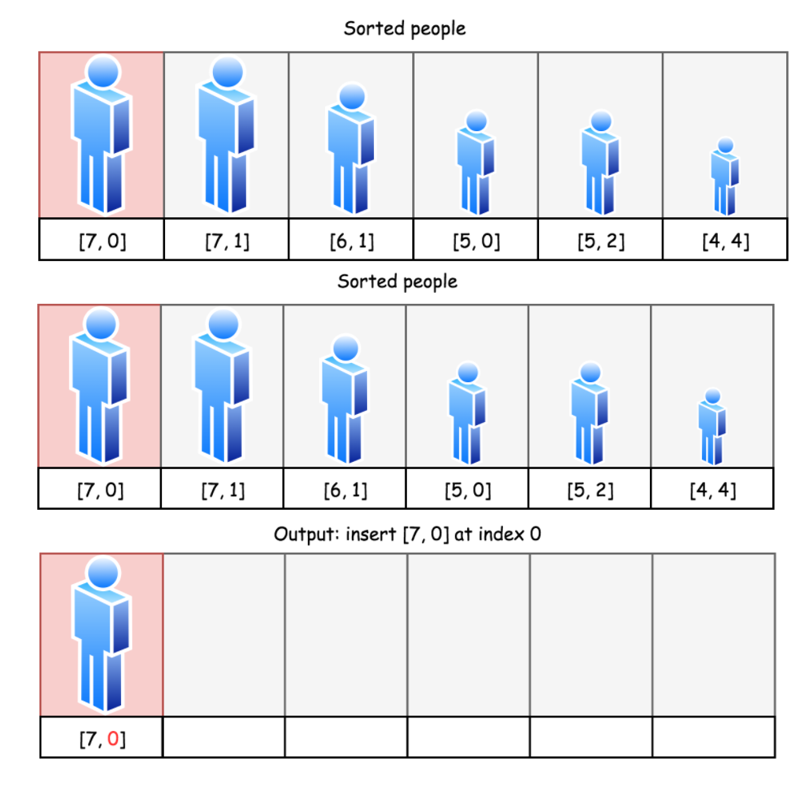
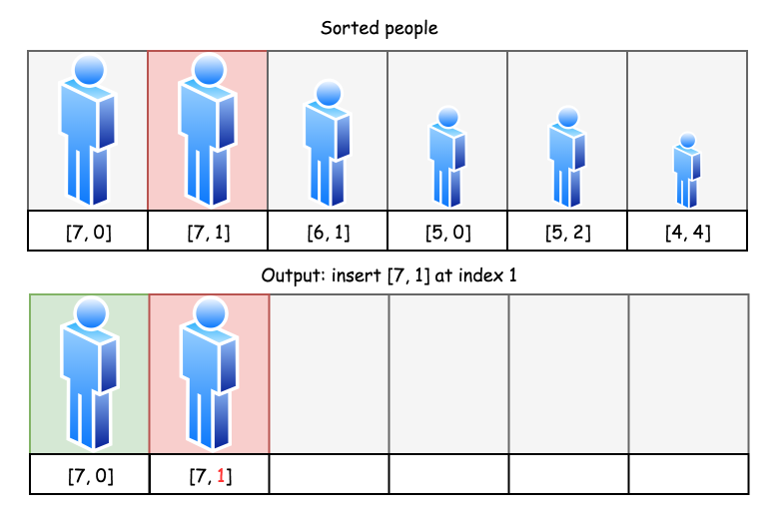
// [7,0], [7,1], [6,1], [5,0], [5,2], [4,4]
// 再一个一个插入。
// [7,0]
// [7,0], [7,1]
// [7,0], [6,1], [7,1]
// [5,0], [7,0], [6,1], [7,1]
// [5,0], [7,0], [5,2], [6,1], [7,1]
// [5,0], [7,0], [5,2], [6,1], [4,4], [7,1]
sort(people.begin(), people.end(), [](const vector<int>& a, const vector<int>& b) {
if (a[0] > b[0]) return true;
if (a[0] == b[0] && a[1] < b[1]) return true;
return false;
});
vector<vector<int>> res;
for (auto& e : people) {
res.insert(res.begin() + e[1], e);
}
return res;
}
};
3.2.1 设计思路
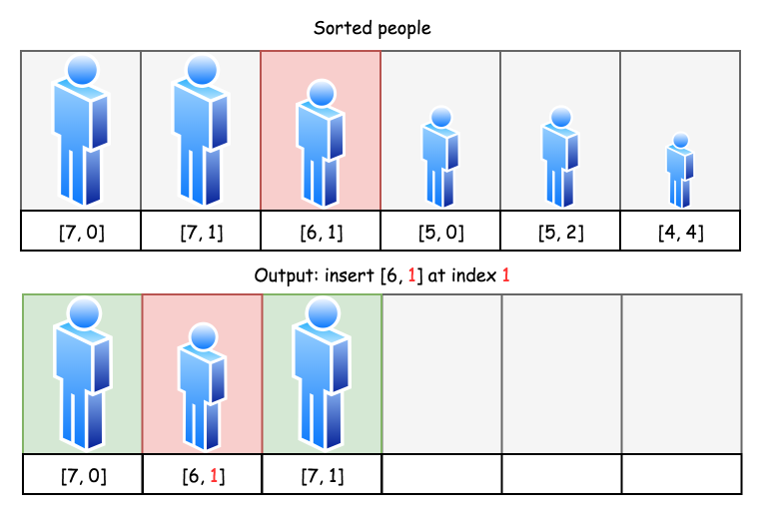
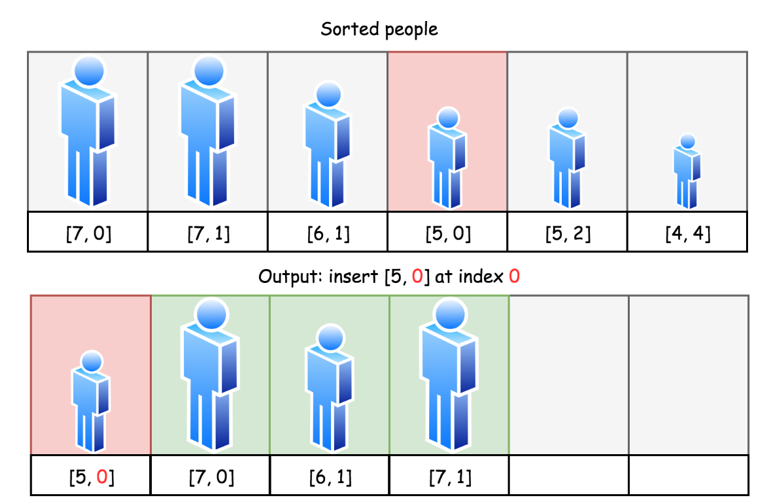

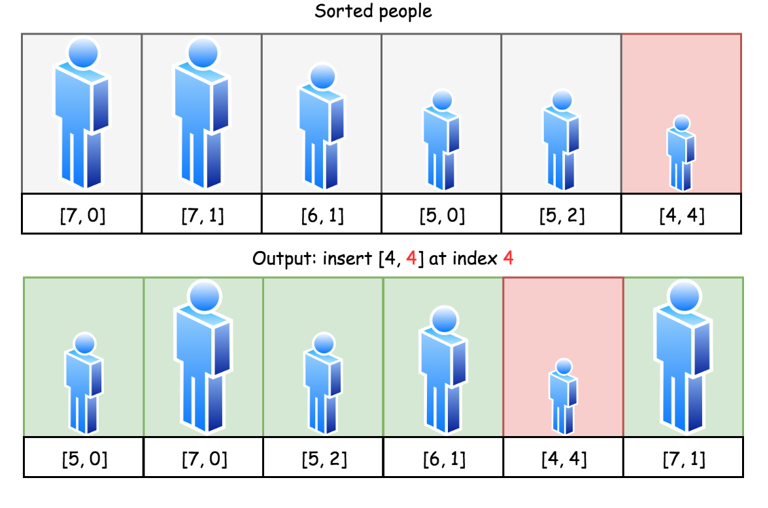
时间复杂度:O(N²) 排序使用了O(NlogN) 的时间,每个人插入到输出队列中需要O(k) 的时间,其中 k 是当前输出队列的元素个数
空间复杂度:O(N) 输出队列使用的空间
3.2.2 伪代码
按高度 h 降序排列;
if(h相同)
按 k 值的升序排列;
for(读取people)
{
根据k找到相应插入位置插入list;
}
return 输出队列;
3.2.3 运行结果
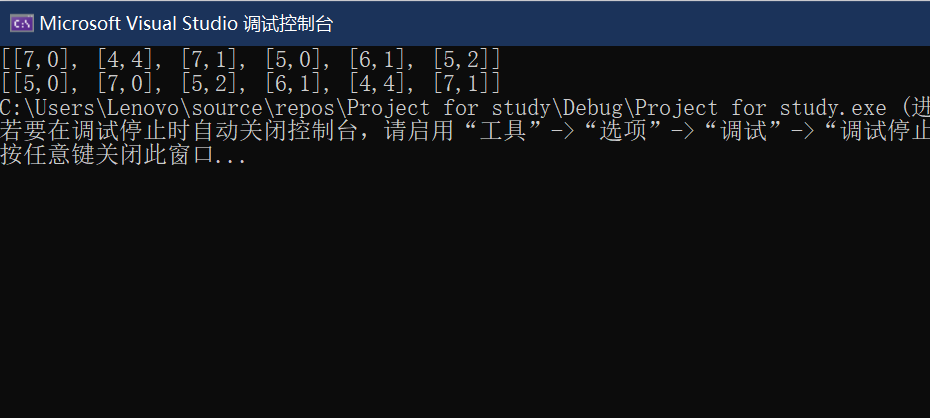
3.2.4 分析该题目解题优势及难点
优点
1.代码运用了各种c++容器,使得代码量变得很少,理解起来也很方便
2.运用贪心算法,思路简洁明了
难点
1.题目又是难懂,一开始看题目没明白是怎么回事,说的是身高应该降序排列为什么[5,0]会在[7,0]的前面,然后看了题解用的贪心算法,粗略看一遍之后也还是没明白是怎么个算法,然后再看一遍才明白过来,题目确实有点难想
2.对于C++的容器以及函数的应用比较多



