DS博客作业02--线性表
0.PTA得分截图

1.本周学习总结
1.1 总结线性表内容
1.1.1 顺序表相关
- 顺序表结构体
顺序表结构体包含元素和顺序表的长度length,其中元素既可以用数组的方式存储,也可以用指针指向元素的基地址

- 顺序表基本操作
- 初始化顺序表:
int i;
L=new list;
L->length=n;
for(i=0;i<n;i++)
cin>>L->data[i];
-
销毁线性表:
- 该运算结果是释放线性表L占用的内存空间
delete L;
-
判断是否为空表:
- 该运算返回一个值表示L是否为空表,若是返回true,不是则返回false
bool ListEmpty(SqList *L)
{
return(L->length==0);
}
-
求线性表长度:
return(L->length); -
输出线性表L:
需要判断表是否为空哦
int i;
for(i=0;i<L->length;i++)
cout<<L->data[i]
-
顺序表查找:
- 体现了顺序表的随机存取特性
for(int i=0;i<L->length;i++)
{
if(L->data[i]==想要查找的数据)
return i+1;//返回元素的逻辑位序
}
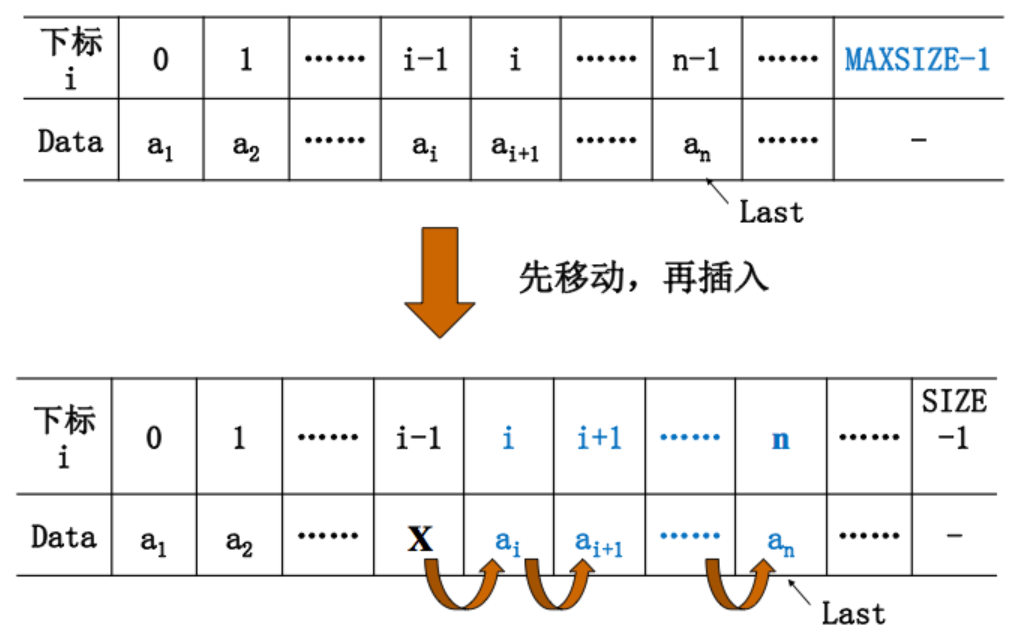
- 顺序表插入:
对于本算法来说,元素移动的次数不仅与表长L->length=n有关,而且与插入位置i有关
1.当i=n+1时,移动次数为0(即算法最好时间复杂度为O(1)
2.当i=1时,移动次数为n,达到最大值(即算法最坏时间复杂度为O(n)
int i,j;
for(j=L->length;j>i;j--)
{
L->data[j]=L->data[j-1];
L->data[j]=要插入的数据;
L->length++;
}
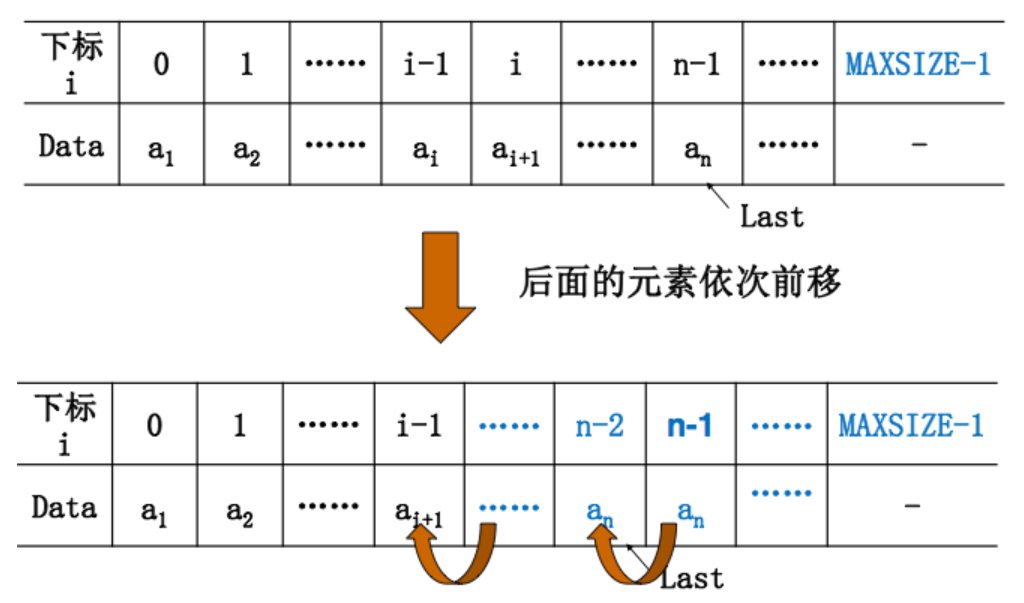
- 顺序表删除:
对于本算法来说,元素移动的次数也与表长n和删除元素的位置i有关:
1.当i=n时,移动次数为0(即算法最好时间复杂度为O(1)
2.当i=1时,移动次数为n-1(即算法最坏时间复杂度为O(n)
int i,j;
要删除的数据=L->data[i];
for(j=i;j<L->length-1;j++)
L->data[j]=L->data[j+1];
L->length--;
- 顺序存储结构的优缺点:
优点:
1.逻辑相邻,物理相邻
2.无需为表示表中元素之间的顺序关系增加额外的存储空间
3.可以随机存取任意一个元素
4.存储空间使用紧凑
缺点:
1.插入删除需要移动大量元素(除了在表尾进行操作)
2.预先分配空间要按最大空间分配,容易造成浪费
3.表容量难以扩充
1.1.2 单链表相关
- 链表结构:
- 节点=数据元素+指针
- 数据元素:存放数据
- 指针:存放该节点下一个元素的存储位置
for example
typedef struct LNode{
int data;
struct LNode *next;
}LNode,*LinkList;
TALK ABOUT: 在链表中设置头结点的优点?
1.便于首元结点的处理
2.便于空表和非空表的统一处理
- 单链表基本操作
- 构建空表:
L=new LNode;
L->next=NULL;
- 头插法建立单链表:

具体代码示例
int i;
int num;
LinkList p;
L = new LNode;
L->next = NULL;
for (i = 0;i < n;i++)
{
cin >> num;
p = new LNode;
p->data = num;
p->next = L->next;
L->next = p;
}
- 尾插法建立单链表:

具体代码示例
int i;
int num;
LinkList p, tail;
L = new LNode;
L->next = NULL;
tail = L;
for (i = 0;i < n;i++)
{
p = new LNode;
cin >> num;
p->data = num;
tail->next = p;
tail = p;
}
tail->next = NULL;
-
销毁线性表:
- 与顺序表不同,因为单链表的节点是一个个申请的,所以不能一下子全部delete,需要一个个删除。
LinkList p;
while(L)
{
p=L;
L=L->next;
delete p;
}
-
判断是否为空表:
return (L->next==NULL); -
求线性表长度:
int n=0;
LinkList p=L->next;
while(p)
{
n++;
p=p->next;
}
return (n);
- 输出线性表:
LinkList s = L->next;//s指向首结点
if (s != NULL)
{
cout<<s->data;
s = s->next;
while (s)
{
cout<<" "<<s->data;
s = s->next;
}
}
else
{
printf("空链表!");
}
- 查找第i个节点数据:
int j=0;
LinkList p=L;
while(j<i&&p!=NULL)
{
j++;
p=p->next;
}
data_i=p->data;
- 插入数据:
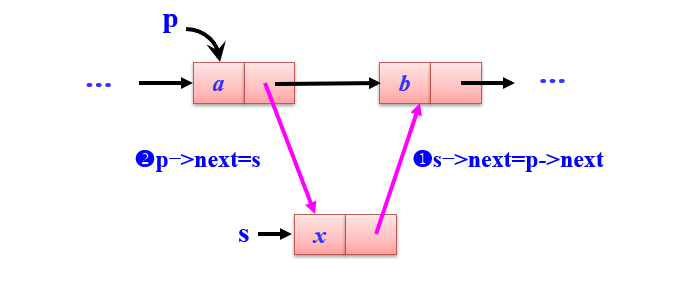
具体代码示例
/*假设p指向ai-1,s指向e*/
s=new LNode;
s->data=e;
s->next=p->next;
p->next=s;
- 删除数据:
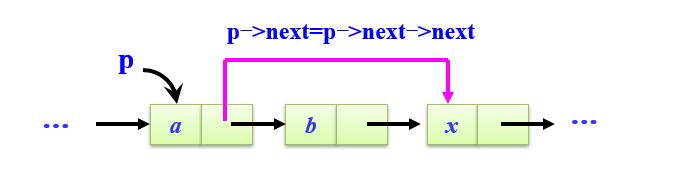
q=p->next;
p->next=q->next;
e=q->data;
delete q;
- 有序递增排列带头节点的单链表L
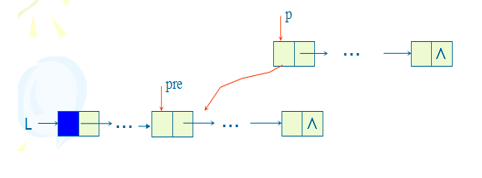
LinkList p,pre,q;
p=L->next->next;//p指向L的第2个数据节点
L->next->next=NULL;//构造只含一个数据节点的有序表
while(p!=NULL)
{
q=p->next;//q保存p节点后继节点的指针
pre=L;//从有序表开头进行比较,pre指向插入p的前驱节点
while(pre->next!=NULL&&pre->next->data<p->data)
{
pre=pre->next;//查找插入p的前驱节点pre
}
p->next=pre->next;//在pre之后插入p
pre->next=p;
p=q;//扫描剩下节点
}
1.1.3 有序表相关
-
有序表含义:
所谓有序表,是指其中所有元素以递增或递减的方式有序排列的线性表 -
有序顺序表的插入算法:
int i=0,j;
while(i<L->length&&L->data[i]<e)
{
i++;
}
for(j=长度n,j>i;j--)
{
L->data[j]=L->data[j-1];
}
L->data[i]=e;
L->length++;
- 有序单链表的插入算法:
LinkList pre=L,p;
while(pre->next!=NULL&&pre->next->data<e)
{
pre=pre->next;
}
p=new LNode;
p->data=e;
p->next=pre->next;
pre->next=p;
- 有序表的归并算法:
TALK ABOUT: 新建一个LC数组,存放LA和LB,然后对LC冒泡或选择法排序,这种做法的时间复杂度是?
设LA的数组长度为m,LB的数组长度为n,则时间复杂度为O((m+n)²)

做法

本算法时间复杂度和空间复杂度都为O(m+n)
- 双链表

双链表特点:
1.从任意一个节点出发可以快速找到其前驱节点和后继节点
2.从任意一个节点出发可以访问其他节点

-
双链表插入:

-
双链表删除:
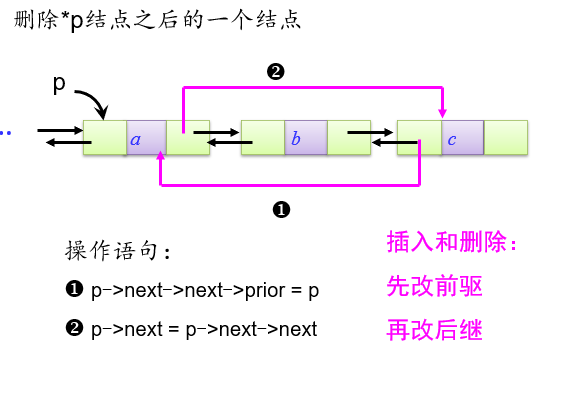
-
头插法建立双链表:
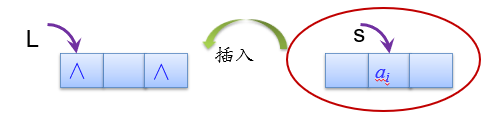
void CreateListF(DLinkNode *&L,ElemType a[],int n)
{ DLinkNode *s; int i;
L=new DLinkNode; //创建头结点
L->prior=L->next=NULL; //前后指针域置为NULL
for (i=0;i<n;i++) //循环建立数据结点
{
s=new DLinkNode;
s->data=a[i]; //创建数据结点*s
s->next=L->next; //将*s插入到头结点之后
if (L->next!=NULL) //若L存在数据结点,修改前驱指针
L->next->prior=s;
L->next=s;
s->prior=L;
}
}
- 尾插法建立双链表:
void CreateListR(DLinkNode *&L,ElemType a[],int n)
{ DLinkNode *s,*r;
int i;
L=new DLinkNode; //创建头结点
L->prior=L->next=NULL; //前后指针域置为NULL
r=L; //r始终指向尾结点,开始时指向头结点
for (i=0;i<n;i++) //循环建立数据结点
{
s=new DLinkNode;
s->data=a[i]; //创建数据结点*s
r->next=s;
s->prior=r; //将*s插入*r之后
r=s; //r指向尾结点
}
r->next=NULL; //尾结点next域置为NULL
}
- 循环链表
- 循环单链表含义:
将表中尾结点的指针域改为指向表头结点,整个链表形成一个环。由此从表中任一结点出发均可找到链表中其他结点。
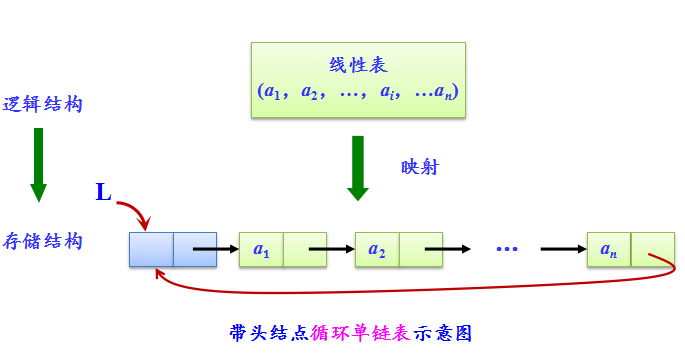
-
单链表特点:

-
循环双链表:
与循环单链表比较:
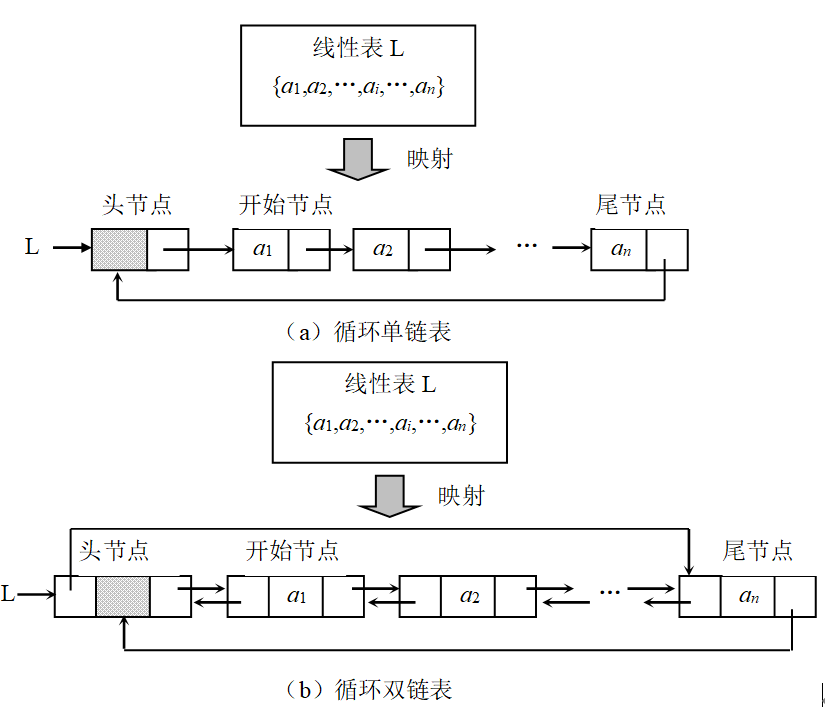
与非循环双链表比较:

1.2 谈谈你对线性表的认识及学习体会
线性表主要分为顺序存储结构和链式存储结构两种。其中顺序存储结构主要运用的是我们比较熟悉的数组的写法,而链式存储结构则运用的是链表。其实从上学期接触链表的时候就觉得链表这玩意有点乱(现在也觉得,但是这学期开始通过更加全面详细的教学,相对起上学期就不会觉得那么力不从心了,很多一开始没搞懂的链关系也解开了。随着学习的深入,调试的难度跟之前比起来也会大一些,没办法第一时间找到问题所在。经过pta的练习,能够对一些常出现的问题进行总结:如指针域未置空,申请空间失败。一开始写pta,写不出来的时候还是会参考网络上的代码,但是后来有好转。最大的体会是,对于程序当中每一句语句的意思都要理清它为什么要这样写,它的思路是什么,强行硬套就像背题,脱离模板就会出错。
2.PTA实验作业
2.1 顺序表删除重复元素
设计一个算法,从顺序表中删除重复的元素,并使剩余元素间的相对次序保存不变。
输入格式: 第一行输入顺序表长度。 第二行输入顺序表数据元素。中间空格隔开。
输出格式:数据之间空格隔开,最后一项尾部不带空格。
输出删除重复元素后的顺序表。
2.1.1 代码截图
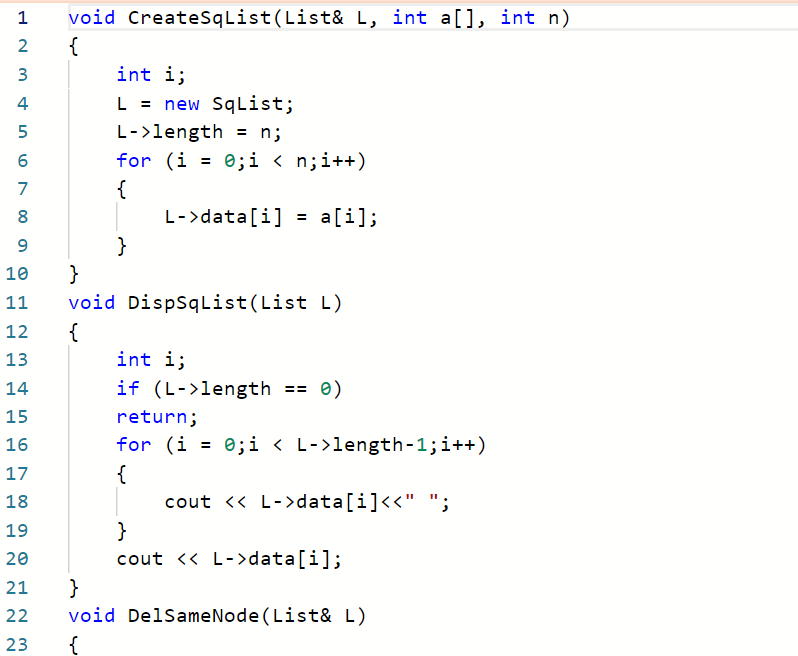

2.1.2 本题PTA提交列表说明

首先部分正确是因为有一个测试点“空表”没过,当初以为是表中全部都是重复数据的时候输出为空表,结果不是 应该是在顺序表长度为0的时候要return回去(不知道这样理解对不对 然后我在输出函数里补充了一个条件:if(L->length==0) return 这样就过了测试点
本题思路大概就是i用来遍历,然后j用来比较,当第i个数据与第j个数据相等时,用k来进行数组左移 这时候要注意循环条件要-1,要不然数组会越界,然后长度也要跟着-1
2.2 链表倒数第m个数
已知一个带有表头节点的单链表,查找链表中倒数第m个位置上的节点。
输入要求:先输入链表结点个数,再输入链表数据,再输入m表示倒数第m个位置。
输出要求:若能找到则输出相应位置,要是输入无效位置,则输出-1。
2.2.1 代码截图

2.2.2 本题PTA提交列表说明

首先部分正确是因为审题不认真(傻了傻了 题目中说要输出-1我就在原来的代码上直接cout<<"-1"了,后来发现其实是要return -1,输出的话题目提供的代码已经写好了 害
然后我这题的思路是逆转链表再进行查找第m个数,因为逆转之后原来倒数第m个数就会变成正数的第m个数,这样就会比较好找了
2.3 两个有序序列的中位数
已知有两个等长的非降序序列S1, S2, 设计函数求S1与S2并集的中位数。有序序列A0,A1,⋯,AN−1的中位数指A(N−1)/2的值,即第⌊(N+1)/2⌋个数(A0为第1数)。输入分三行。第一行给出序列的公共长度N(0<N≤100000),随后每行输入一个序列的信息,即N个非降序排列的整数。数字用空格间隔。
2.3.1 代码截图
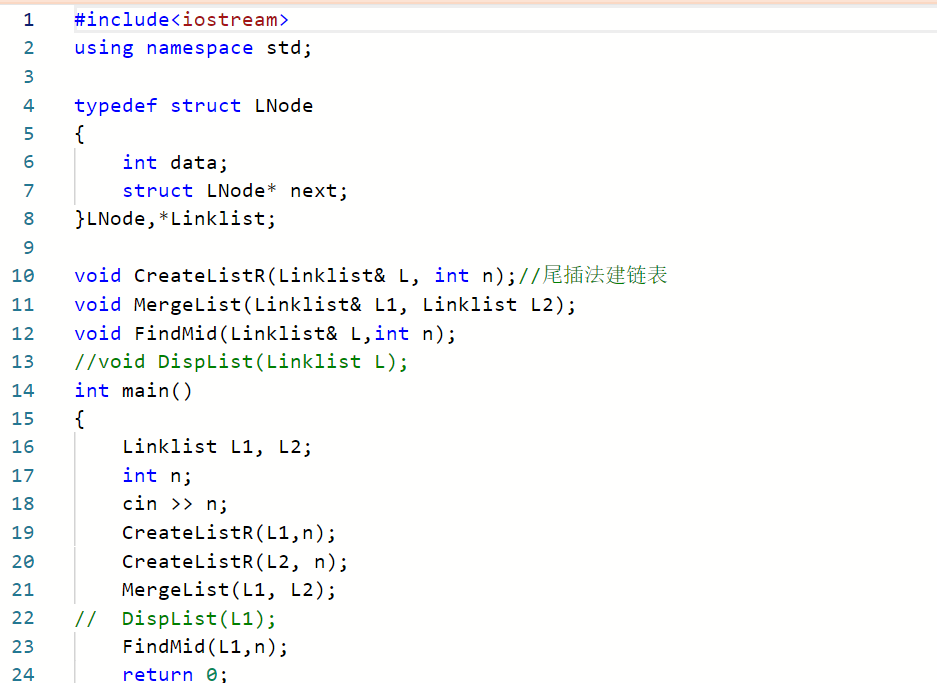

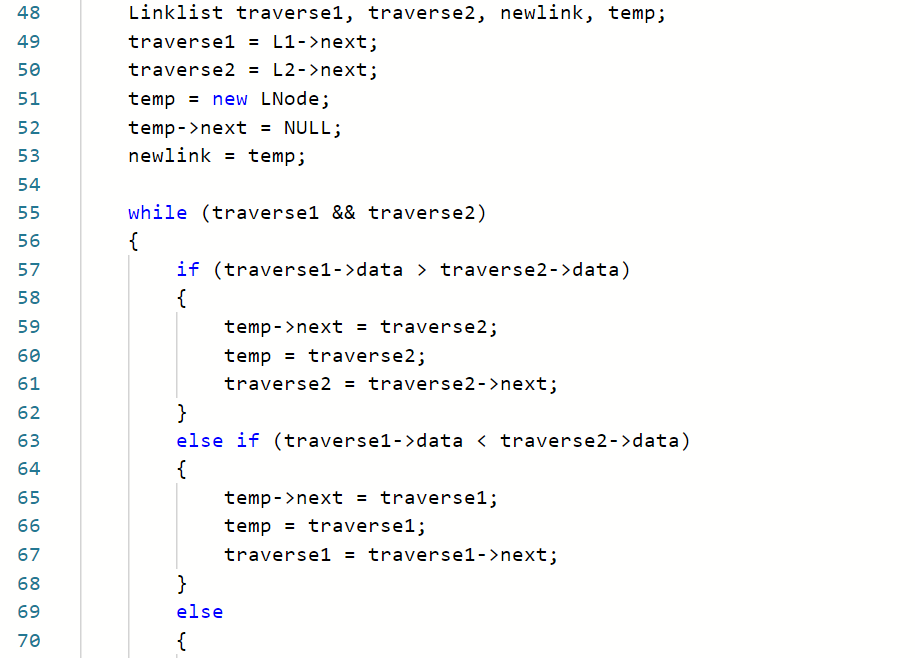


2.3.2 本题PTA提交列表说明

首先编译错误的问题是因为PTA中这一题好像是先默认了c的编译器,然后我的代码中有c++的语法导致不能通过编译,于是我把PTA的编译器改成c++了(不知道行不行emmm
然后这题我的大概思路是先输入两个链表数据,然后按升序合并两个链表,再查找中位数
我在vs上编译的时候错误主要有两点
第一点是排序问题,因为中位数的查找是要包括重复数据的,然后我按之前的写法来写的话重复数据就会被删除导致中位数查找不准确
第二点是查找中位数的问题,排序完成之后我查找出来的数字不知道为什么老是3,然后我就输出了一下链表看是不是我的链表有问题,看完之后发现链表很正常,然后我就调试看发现是查找的位置不对,我一开始直接按题目上给出的(N+1)/2来查找了,后来发现两条链合并找中位数的话应该是(2N-1)/2
3. 阅读代码
3.1 题目及解题代码
-
题目:

-
代码:
ListNode *addTwoNumbers(ListNode *l1, ListNode *l2)
{
int digit = 0;
int carryDigit = 0;
ListNode *res = new ListNode(0);
ListNode *tmpRes = res;
//carryDigit为进位数
while (l1 || l2 || carryDigit)
{
int tmpSum = 0;
if (l1)
{
tmpSum += l1->val;
l1 = l1->next;
}
if (l2)
{
tmpSum += l2->val;
l2 = l2->next;
}
tmpSum += carryDigit;
digit = tmpSum % 10;
carryDigit = tmpSum / 10;
ListNode *newLocation = new ListNode(digit);
tmpRes->next = newLocation;
tmpRes = tmpRes->next;
}
//删除哑节点
tmpRes = res->next;
delete res;
return tmpRes;
}
3.1.1 设计思路
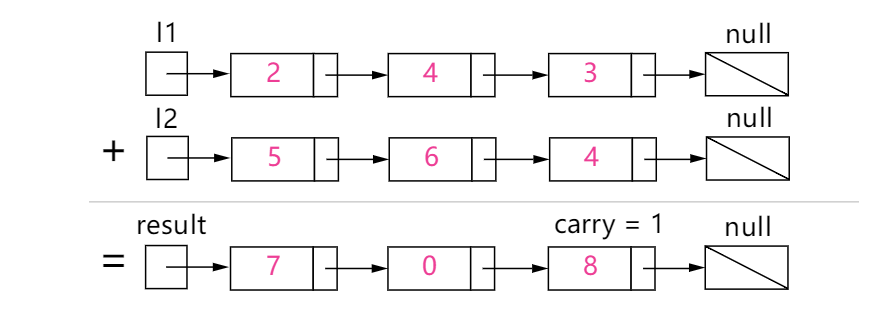
时间复杂度:O(n)
空间复杂度:O(n)
3.1.2 伪代码
将进位CarryDigit初始化为0;
ListNode *addTwoNumbers(ListNode *l1, ListNode *l2)
{
while(A or B or 进位数)
if(A非空)得出sum的值 A=A->next
if(B非空)得出sum的值 B=B->next
设定tmpSum=A+B+CarryDigit
更新进位的值,CarryDigit = sum / 10
创建一个新结点newLocation,并将其设置为当前结点的下一个结点,然后将当前结点前进到下一个结点
返回哑结点的下一个结点
}
3.1.3 运行结果
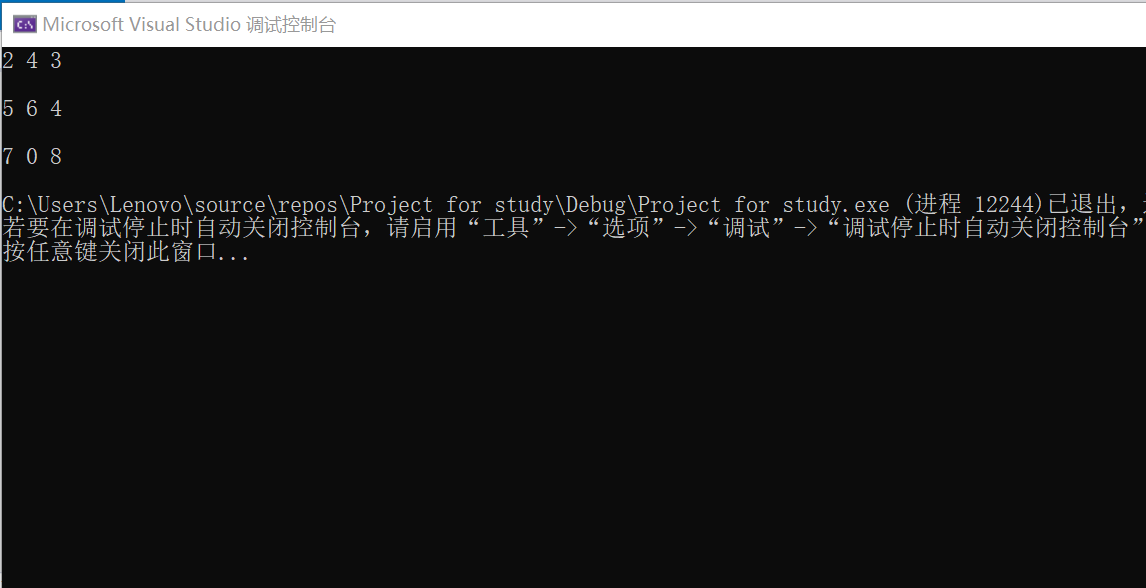
3.1.4 分析该题目解题优势及难点
优势:
1.使用哑结点来简化代码。如果没有哑结点,则必须编写额外的条件语句来初始化表头的值。
2.评论有一个思路是:将链表的数字转换成实际的数字(假设是逆序的,那就是[3,4.2] -> 243),然后将两数做运算(加减乘除),得到的数字再按位,按顺序(正序或逆序)转换成链表 但是这样做会造成int溢出、运行超时等问题,而且时间复杂度较高,而给出的代码能很好的解决这个问题
难点
1.要考虑进位数的可能性,进位数CarryDigit必然是0或1,这是因为两个数字相加(考虑到进位)可能出现的最大和为 9 + 9 + 1 = 19。
2.要考虑的特殊情况较多,例如当一个列表比另一个列表长时、出现空列表时、求和运算最后可能出现额外的进位,这一点很容易被遗忘。
3.2 题目及解题代码
-
题目:

-
代码:
TreeNode* sortedListToBST(ListNode* head)
{
return buildTree(head, nullptr);
}
TreeNode * buildTree(ListNode* head, ListNode * tail)
{
if(head == tail) return nullptr;
ListNode* slow = head, *fast = head;
while(fast != tail && fast->next != tail)
{
slow = slow->next;
fast = fast->next->next;
}
TreeNode * root = new TreeNode(slow->val);
root->left = buildTree(head, slow);
root->right = buildTree(slow->next, tail);
return root;
}
3.2.1 设计思路
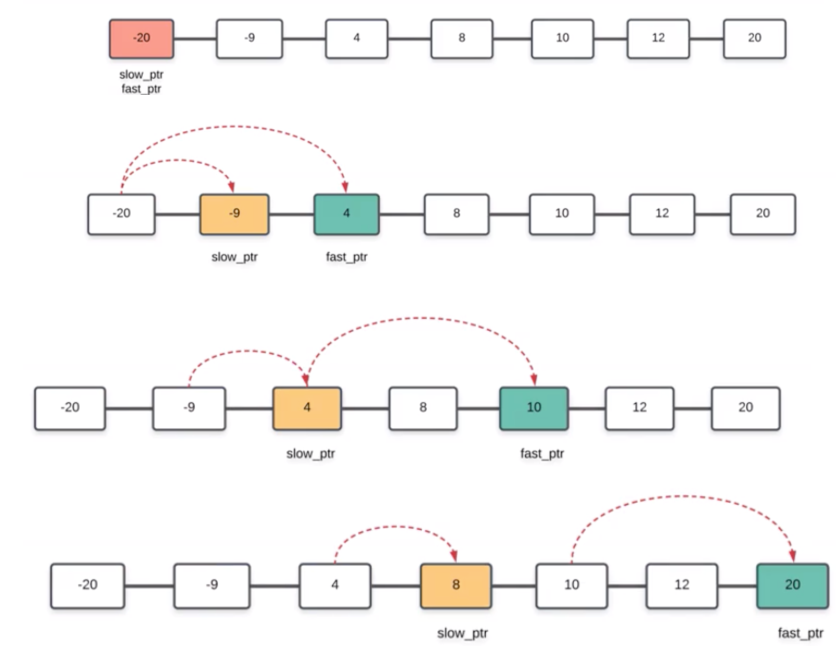

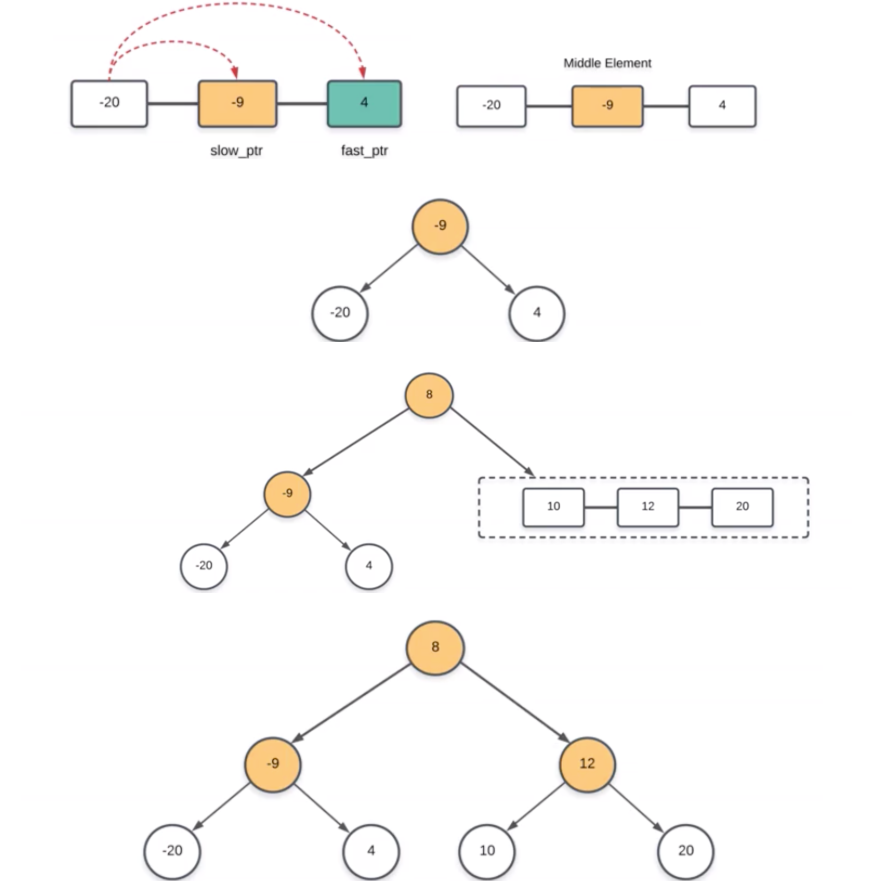
时间复杂度:O(NlogN)
空间复杂度:O(logN)
3.2.2 伪代码
TreeNode * buildTree(ListNode* head, ListNode * tail)
{
if(为空链表)返回null;
定义快慢指针;
while(fast != tail && fast->next != tail)
{
slow = slow->next;
fast = fast->next->next;
} //快指针每次走两步,慢指针每次走一步,当快指针走到链表尾部,慢指针就指向了中间位置。
//此时慢指针指向中间节点
定义root = new TreeNode(slow->val);
root->left = buildTree(head, slow);
root->right = buildTree(slow->next, tail);
return root;
}
3.2.3 运行结果
这里我把左右子树分开输出
3.2.4 分析该题目解题优势及难点
优势:
1.不需要数组辅助
2.利用快慢指针寻找中值节点,降低时间复杂度
3.不需要切割链表,[head, tail) 用于界定一个半开半闭区间,与断链比起来更方便
难点:
1.递归写法要观察本级递归的解决过程,比较抽象
2.要注意题目中提出的高度平衡条件
3.题目中所给出的输出null不是很理解 不知道为啥要输出一个null 😦



