伯努利分布及衍生分布、随机游走

伯努利实验

伯努利实验概念及性质

定义：事件域为：$\mathcal{F}=\{\varnothing ,A,\overline{A},\mathrm{\Omega }\}$，只两种可能结果的试验称为伯努利实验。
现考虑重复n次独立试验的伯努利实验（这里每个$A$概率不变），这种实验称之为n重伯努利实验，记为$E^n$。
其样本点形如：

$$({\hat{A}}_1,{\hat{A}}_2,...,{\hat{A}}_n)$$

其中每个都有两种可能取值。易得样本点一共有$2^n$。概率空间易得不再赘述。

伯努利分布

伯努利分布（Bernoulli Distribution）是一种离散型概率分布，它用于描述只有两种结果（例如成功和失败）的随机试验。伯努利分布可以用一个参数$p$来描述成功的概率。概率分布可简单表示为：

$$P(X=k)=kp+(1-k)(1-p)$$

其中k仅有0，1两个取值。这样写概率的好处在于：可以用于最大似然估计中的求导。
伯努利分布的期望和方差分别为：

$$E(X)=p\cdot 1+(1-p)\cdot 0=p$$

$$Var(X)=(EX{)}^2-E{X}^2=p(1-p)$$

伯努利分布通常用于二元分类问题中，例如预测一个事件是否发生、一次抛硬币的结果等。

二项分布

如果有多次独立的伯努利试验，可以使用二项分布（Binomial Distribution）来描述（简记为B）。
若记$B_k$为n重伯努利实验中事件$A$正好出现$k$次。则：

$$P(B_k)=C_n^k{p}^k{q}^{n-k}$$

二项分布的重要性质

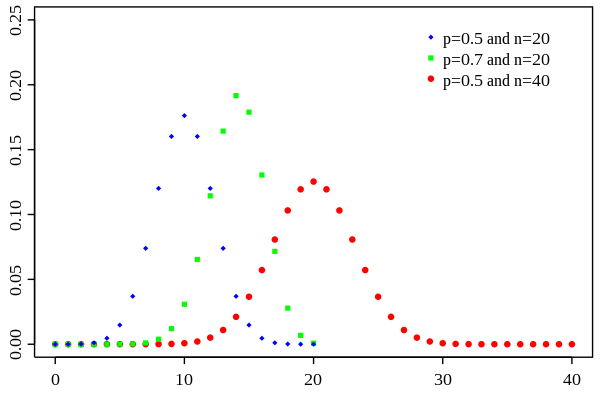
• 概率函数的形状：二项分布的概率函数呈现出类似钟形曲线的形状，当$p=0.5$时，概率函数的峰值达到最高。
  
• 期望和方差：二项分布的期望和方差分别为$E(X)=np$和$Var(X)=np(1-p)$
  由于每次试验独立，期望与方差可以简易地由伯努利分布的期望与方差推出。
  若要依据其概率分布来推，则二项分布期望推导如下：

$$E(X)=\sum _{k=0}^{n}kP(B_k)=\sum _{k=0}^{n}k{C}_n^k{p}^k(1-p{)}^{n-k}$$

而

$$\sum _{k=0}^{n}k{C}_n^k{p}^k(1-p{)}^{n-k}=\sum _{k=0}^n\frac{kn!}{k!(n-k)!}{p}^k(1-p{)}^{n-k}$$

$$=np\sum _{k=1}^n\frac{(n-1)!}{(k-1)!(n-k)!}{p}^{k-1}(1-p{)}^{n-k}$$

上式右边部分是$n-1$次实验抽到$k-1$个的概率对k求和，从而为1。
二项分布的方差推导如下：

$$E(X^2)=k(k-1)\sum _{k=0}^n{C}_n^k{p}^k(1-p{)}^{n-k}+k\sum _{k=0}^n{C}_n^k{p}^k(1-p{)}^{n-k}$$

与上面求期望的同理，把$k(k-1)$乘进$C$的表达式即可。这个构造我认为非常有用，这样的话即便是$E(X^3)$，也可以拆成$k(k-1)(k-2)+ak(k-1)+bk$的形式进一步求解。回到原话题，由上易得

$$E(X^2)=n(n-1)p^2+np$$

从而最终得到$Var(X)=np(1-p)$

• 大数定律：二项分布具有大数定律，即当试验次数$n$趋近于无穷大时，二项分布的概率函数逐渐趋近于正态分布

• 中心极限定理：二项分布满足中心极限定理，即当试验次数$n$足够大时，二项分布可以近似看作正态分布

几何分布

现在讨论在伯努利实验中手册成功出现在第k次实验的概率。记第k次实验出现$A$的事件为$W_k$，有：

$$P(W_k)=q^{k-1}p$$

几何分布性质

• 无记忆性：几何分布具有无记忆性，即在已知前$k$次试验失败的情况下，下一次试验仍然是独立的伯努利试验，成功的概率仍然是$p$
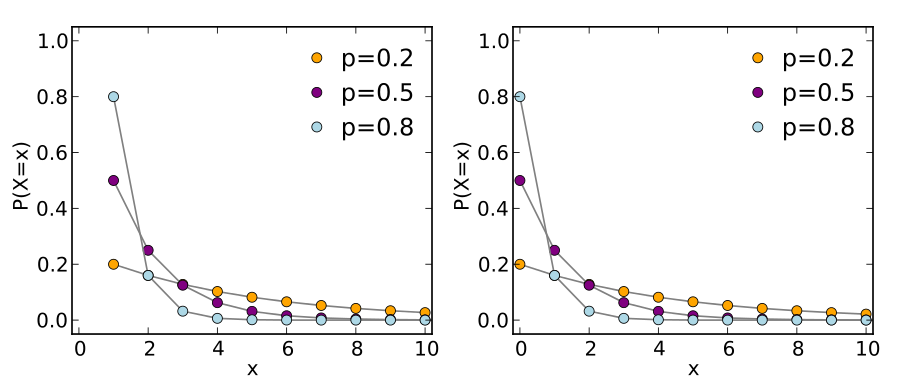
• 概率函数的形状：几何分布的概率函数呈现出右偏斜的单峰形状，随着等待次数$k$的增加，概率逐渐减小
  
• 期望和方差：几何分布的期望为$E(X)=\frac{1}{p}$，方差为$Var(X)=\frac{1-p}{p^2}$
  期望可由高中数列错位相减法处理，是比较易得的。方差稍微有些变化：

$$E(X^2)=\sum _{k=1}^{\mathrm{\infty }}{k}^{2}p{q}^{k-1}=p(\sum _{k=1}^{\mathrm{\infty }}k{q}^k{)}^{\prime }$$

接下来的部分就不写了，总之容易得到$Var(X)$。

帕斯卡分布

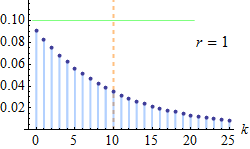
让我们以$C_k$表示第r次成功发生在第k次实验这一事件。

$$P(C_k)=C_{k-1}^{r-1}{p}^r{q}^{k-r}$$

这个概率分布被称之为帕斯卡分布。
典中典的就是分赌注问题。

帕斯卡分布与分赌注问题（Gambler's Ruin Problem）有着密切的联系。分赌注问题的确是一个比较正统的概率论问题，它也被看做是概率论诞生的事件。问题描述很简单，说甲乙两人下赌注，然后反复进行双人赌局，约定谁先赢$𝑡$局者获胜。显然，有限赌局后一定可以分出胜负，有趣的问题是：赌局在甲胜$r$局、乙胜$s$局后被迫中止，那赌注该如何分配？一种最简单粗暴的方法就是按照$r:s$的比例关系分配，这种方法只是符合了含糊的直觉，完全经不起推敲。
但用帕斯卡分布的模型来看，就经得起推敲了。可从3个角度确定甲赢的概率：
（1）根据乙赢的次数或总次数；（2）根据乙赢时甲赢的次数；（3）接下来的$m+n-1$局里甲胜的局数。它们其实是相等的。依照概率分赌注，就会显得相当合理了。

随机游走

随机游走（Random Walk）是指在规定的状态空间中，按照一定的概率分布，随机地向某个方向前进的过程。随机游走可以在一维、二维或更高维的状态空间中进行。

在随机游走中，每一步的移动通常是独立的，且每一步的概率分布只依赖于当前的状态，与之前的状态或历史无关。在一维随机游走中，例如，每一步可以向左或向右移动一个单位距离，且向左或向右的概率相等，即$p=0.5$。在二维随机游走中，每一步可以向上、向下、向左或向右移动一个单位距离，且四个方向的概率相等，即$p=0.25$。

若质点可以在整个数轴的整数点上游动，则称这种随机游走为无限制随机游走。若在某点有个吸收壁，质点到这就不再动了，则称之为有吸收壁的随机游走。

无限制随机游走

《随机过程》教科书给出了一维简单随机游走随机变量的数学模型

$$S=X_1+X_2+...+X_n$$

易得$E(S)=0,Var(S)=n$
表明一维简单随机游走$S_n$的方差与步数$n$成正比，因此，一维简单随机游走是一个类似于物理学布朗运动的扩散过程。
方差是用来刻画随机变量偏离均值分散程度的数字特征，度量的是所有样本轨道（小球或醉汉）偏离均值的发散程度，因此，方差表明：随着步数n的增加，大量一维简单随机游走的小球会远离原点。

n次移动移动到k(k可以为负整数)的概率为：

$$P(R=k)=C_n^{\frac{n+k}{2}}{q}^{\frac{n-k}{2}}{p}^{\frac{n+k}{2}}$$

其中p为向上移动的概率，$p+q=1$（注意n、k必须同奇偶）。
来一些问题：

• 无限制随机游走的期望距离：

$$E(R)=E(|\sum _{i=1}^n{X}_i|)$$

待补充：似乎是没有比较简洁的答案

• 无限制随机游走回到原点的期望步数：
  待补充：似乎是没有比较简洁的答案
• 一开始在数轴0位置，有P概率往右走，Q概率往左走，问第一次到达位置n的期望步数

二维推广：

• 首先是无限制随机游走的期望距离

$$E(R)=E(\sqrt{|\sum _{i=1}^n{X}_i{|}^2+|\sum _{i=1}^n{Y}_i{|}^2})$$

待补充：似乎是没有比较简洁的答案

有吸收壁的随机游走

经典面试概率题
假定质点在0时刻位于$a$，在$x=0$，$x=a+b$处各有一个吸收壁，我们来求在两个吸收壁被吸收的概率，用的是差分方程法。
若以$q_n$记质点初始位置为n而最终在$a+b$点被吸收的概率，我们易得：

$$q_0=0,q_{a+b}=1$$

若某时刻质点位于$x=n$，想要让他被$x=a+b$处吸收，有两种实现方法：要么接下去一次向$a+b$处移动，然后再移动被吸收；要么接下来一次向0移动，然后再移动被吸收。据此我们可列出：

$$q_n=p{q}_{n+1}+q{q}_{n-1},n=1,2,...,a+b-1$$

令$q_{n+1}-q_n=c_n$，可写作：

$$c_n=\frac{q}{p}{c}_{n-1}$$

当$q=p$时，q成等差数列，易得$q_n=\frac{n}{a+b}$。
当$q!=p$时，可解得$q_n=\frac{1-r^n}{1-r^{a+b}}$，其中$r=\frac{q}{p}$

同样的思路——状态n的概率与状态n-1/n+1的概率有关——还可以用到许多问题的求解上