单层卷积网络
如何构建卷积神经网络的卷积层？
如下图，6x6x3的RGB图像与2个3x3x3的卷积核做卷积，得到2个4x4的矩阵，然后再加上偏置b（对4x4矩阵每个元素均加上该偏置b），接着将其作为ReLU激活函数的输入，得到2个4x4的矩阵输出。即6x6x3的RGB图像与2个3x3x3的卷积核做卷积会得到一个4x4x2的输出。如果卷积核的数量时10，那么输出大小就是4x4x10。
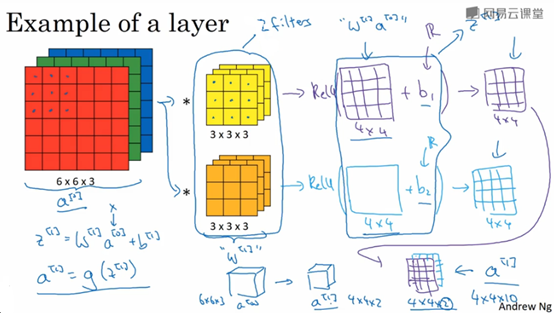
如何计算卷积运算中参数量？假设一层中有10个3x3x3的卷积核，则总共参数有总共有（3 x 3 x 3 + 1）x 10 = 280个参数。如下图所示。
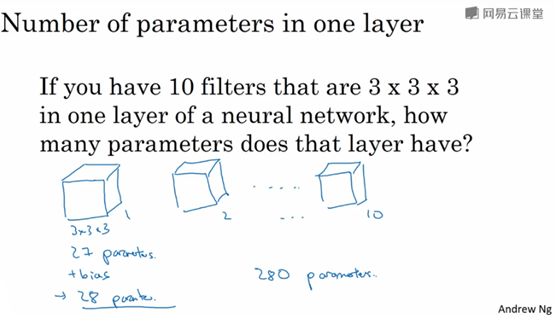
注：不论输入图片有多大，参数量都是一样的。这个有助于避免过拟合。
输入输出尺寸推导公式。如果第l层是卷积层，那么卷积核的通道数与输入的通道数，卷积核的个数等于输出的通道数。输出大小计算方法为(n+2p-f)/s+1。如下图。
注：
1）Filter大小：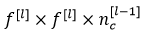
，其通道数等于输入的通道数
2）输出的通道数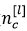
就是filter的个数
总结如下：
m表示batch size
偏差bias在代码中一般表示为一个
的四维向量或者四维张量
简单神经网络示意
假设你有一张图片x，大小为39x39x3；
filter1参数：每个filter大小3x3，stride=1，padding=0，总共有10个filter；
图片x与filter1卷积之后产生37x37x10大小的feature map1；
filter2参数：f=5，s=2，p=0，总共有20个filter；
feature map1与filter2做卷积，得到17x17x20大小的feature map2；
filter3参数：f=5，s=2，p=0，总共有40个filter；
feature map2与filter3做卷积，得到7x7x40大小的feature map3
39x39x3的原图像经过一系列的卷积操作之后，最后输出7x7x40大小的feature map，即为该图像提取了7x7x40=1960个特征。然后将展开（flatten）成1960个单元（即一个1960维的向量），最后经过logistic或者softmax单元，得到最后的分类值。
过程如下图：
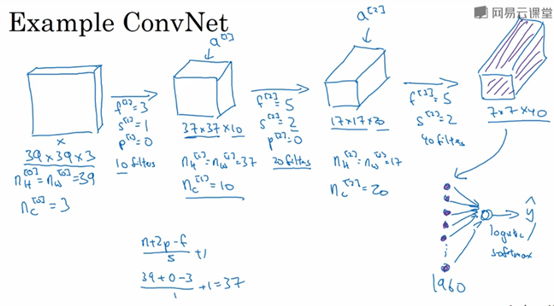
设计卷积神经网络的时候，确定这些超参数比较费功夫，要决定filter的大小、个数，stride，padding等。一般，feature map的大小不断变小，其channel不断的增大。
一个典型的卷积神经网络通常有3层，一个是卷积层（Conv），另一个是池化层（Pooling），最后一个是全连接层（Fully connected，FC）
池化层
用来减缩模型大小，提高计算速度，同时提高所提取特征的鲁棒性。
下图为最大池化（max pooling）示意图。其中，Filter size 2x2 stride=2
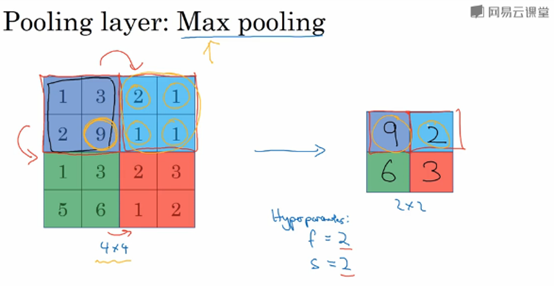
池化层的特点：
有一组超参数，但是没有参数需要学习，一旦确定了f和s，它就是一个固定的运算，梯度下降无需改变任何值。超参数一般是手动设置或者通过交叉验证设置的。
上面的把4x4的输入看做是某些特征的集合，数字大意为着可能提取了某些特定特征。
最大池化可以保留最显著的特征
人们使用最大池化的其中一个原因是，此方法在很多实验中效果都很好
另外一个例子：
最大池化，filter size：3x3，stride=1
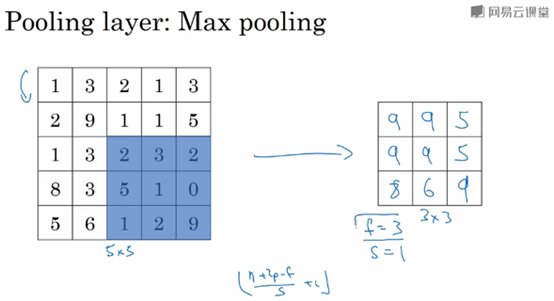
注：
对于输入是多维的情况，输出也是多维的；计算方式是，对每个通道分别执行最大池化过程
平均池化：选取的不是每个filter的最大值，而是平均值。
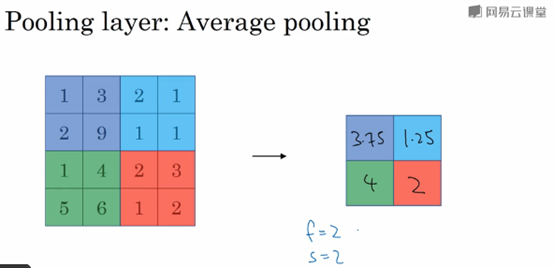
一般来说，目前最大池化比平均池化要更常用
但也有例外，就是深度很深的神经网络，你可以用平均池化来分解规模为7x7x1000的网络表示层，在整个空间内求平均值，得到1x1x1000
一般在最大池化中，使用padding是比较少的，但也有例外。
总结如下：
内容主要来自与：
Andrew Ng的卷积神经网络课程
