举例1:
比如输入是一个32x32x3的图像,3表示RGB三通道,每个filter/kernel是5x5x3,一个卷积核产生一个feature map,下图中,有6个5x5x3的卷积核,故输出6个feature map(activation map),大小即为28x28x6。
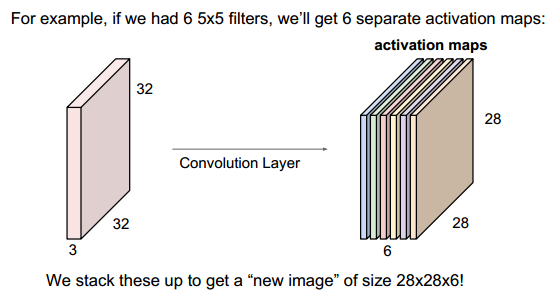
下图中,第二层到第三层,其中每个卷积核大小为5x5x6,这里的6就是28x28x6中的6,两者需要相同,即每个卷积核的“层数”需要与输入的“层数”一致。有几个卷积核,就输出几个feature map,下图中,与第二层作卷积的卷积核有10个,故输出的第三层有10个通道。
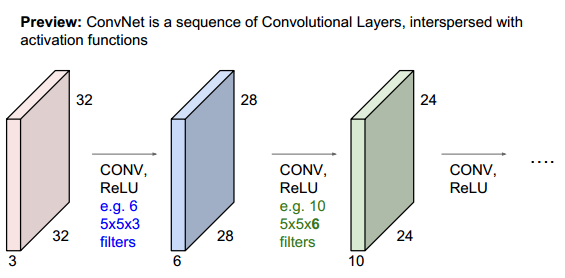
举例2:
NxN大小的输入(暂时不考虑通道数),与FxF大小的卷积核(暂时不考虑个数)做卷积,那么输出大小为多大?计算公式为:(N - F) / stride + 1,其中stride为做卷积是相邻卷积核的距离。

举例3:
当输入为7x7大小,卷积核为3x3,stride=1,在7x7周围补上一圈0(pad=1个像素),那么输出大小为多大?
是7x7。

举例3:
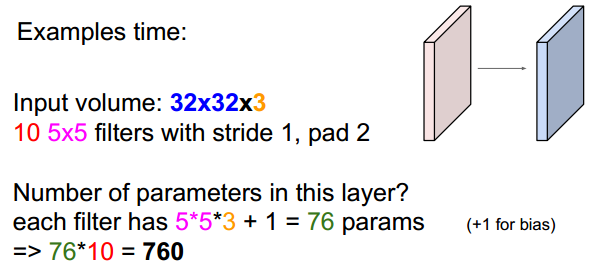
输入为32x32x3,卷积核大小为5x5,总共有10个卷积核,做卷积的时候stride=1,pad=2,那么这一层总共含有多少参数?
每个卷积核含有的参数个数为:5*5*3 + 1 = 76,其中1是偏置bias,由于有10个卷积核,故总参数为76*10=760。
总结:

其中,卷积核的数量K一般是2的整数次幂,这是因为计算方便(计算机计算2^n比较快)
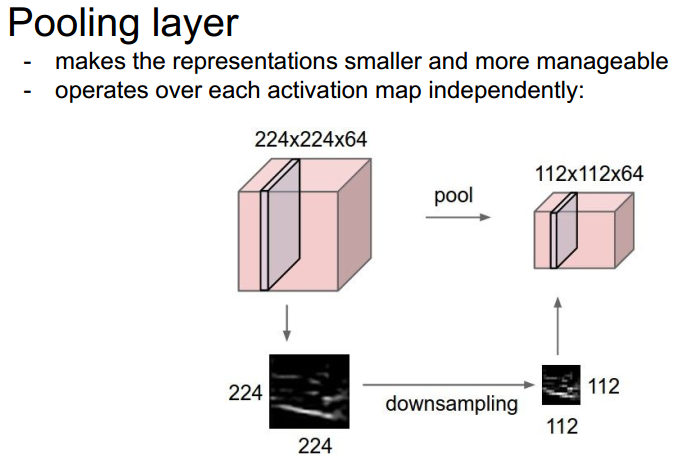
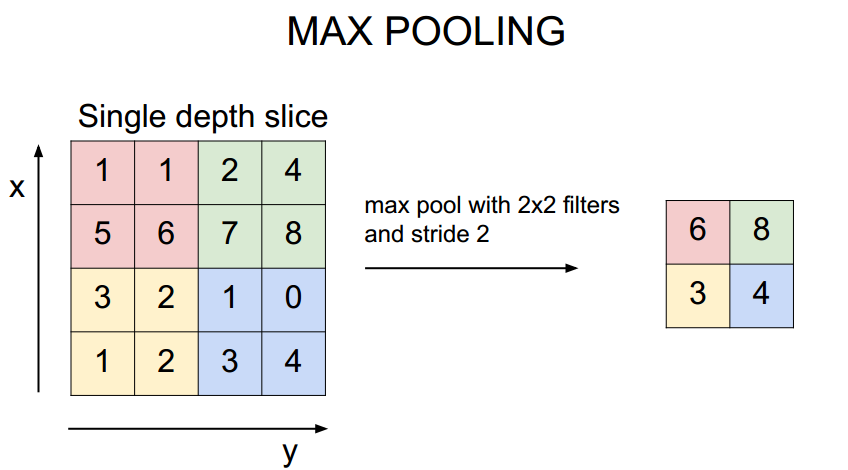
关于池化层的参数计算:

参考:
斯坦福大学CS231N课程PPT
http://cs231n.stanford.edu/slides/2016/winter1516_lecture7.pdf


 浙公网安备 33010602011771号
浙公网安备 33010602011771号