为什么LSTM可以防止梯度消失？从反向传播的角度分析
LSTM：温和的巨人
相比于RNN，虽然LSTM（或者GRU）看上去复杂而臃肿，但是LSTM（或者GRU）在实际中的效果是非常好的，它可以解决RNN中出现的梯度消失的问题。
梯度消失是指，在反向传播时，梯度值随着反向传播呈指数下降，最终造成的影响是越靠近输入的层梯度值越接近0，这些层因此无法得到有效的训练。对于RNN，这意味着无法跟踪任何长期依赖关系。 这是一种麻烦，因为RNN的全部意义在于跟踪长期依赖关系。
接下来介绍为什么LSTM（及其相关的模型）可以解决梯度消失的问题。
下面先介绍LSTM相关的符号。
LSTM的公式如下（省略bias）
梯度消失的情况
为了理解LSTM为什么有帮助，我们需要先理解普通RNN（ vanilla RNNs）中出现的问题。在普通的RNN中，隐含层向量和输出的计算方式如下：
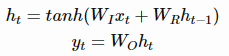
要通过时间进行反向传播（ backpropagation through time）来训练RNN，我们需要计算E关于
的梯度。 总误差梯度等于每一时间步的误差梯度之和。对于时间t，我们可以使用链式法则来推导出误差梯度，如下：
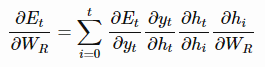
上面的式子中，
的具体形式如下：
关于
的偏导数如下：
其中，diag函数将一个向量转换为对角矩阵。
因此，如果我们通过时间步t来进行反向传播，梯度表示如下：
参考这篇文章（ On the difficulty of training Recurrent Neural Networks ），如果矩阵
的主特征值（ dominant eigenvalue）大于1，那么就会产生梯度爆炸（gradient explodes）；如果小于1，那么就会产生梯度消失（gradient vanishes）。注意到
的值总是小于1，因此如果
的值太小，将不可避免的会造成梯度值变成0；如果的值很大，那么导数/梯度就会变得很大。在实际中，梯度消失更加常见，因此我们更关注于梯度消失问题。
的主特征值（ dominant eigenvalue）大于1，那么就会产生梯度爆炸（gradient explodes）；如果小于1，那么就会产生梯度消失（gradient vanishes）。注意到的值总是小于1，因此如果的值太小，将不可避免的会造成梯度值变成0；如果的值很大，那么导数/梯度就会变得很大。在实际中，梯度消失更加常见，因此我们更关注于梯度消失问题。导数
可以告诉我们当我们改变时刻l（小写的L）的隐层状态时，时刻k的隐层状态将会改变多少。根据上面的数学公式，梯度消失的意思是前面隐藏层（ earlier hidden states）将对后面的隐藏层（later hidden states）不产生影响，这意味着没有学到长期依赖关系（no long term dependencies are learned）。具体的证明可以参考原始的LSTM文章和上面提到的那篇文章。
可以告诉我们当我们改变时刻l（小写的L）的隐层状态时，时刻k的隐层状态将会改变多少。根据上面的数学公式，梯度消失的意思是前面隐藏层（ earlier hidden states）将对后面的隐藏层（later hidden states）不产生影响，这意味着没有学到长期依赖关系（no long term dependencies are learned）。具体的证明可以参考原始的LSTM文章和上面提到的那篇文章。
使用LSTM来防止梯度消失
正如上面提到，造成梯度消失的最大原因就是我们需要计算递归导数
，我们如果可以解决这个问题，那么我们就可以学到长期依赖关系（long term dependencies）
，我们如果可以解决这个问题，那么我们就可以学到长期依赖关系（long term dependencies）针对这个问题，最原始的LSTM是这样解决的：使得递归导数（recursive derivative）的值为常量。在这种情况下，梯度就不会消失或者爆炸。该如何实现这一点呢？LSTM引进了一个单独的cell state
。在最原始的1997年版本的LSTM，的值取决于前一个cell state的值和按input gate加权的更新项（使用input gate的motivation可以参考这篇文章），具体公式如下：
。在最原始的1997年版本的LSTM，的值取决于前一个cell state的值和按input gate加权的更新项（使用input gate的motivation可以参考这篇文章），具体公式如下：
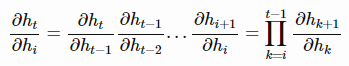
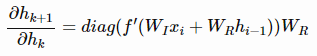
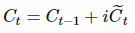
上面的公式效果并不好，原因是cell state可能会增长得无法控制。为了防止这个无限增长，引入了forget gate，公式如下：
一个常见的误解。LSTM为什么可以解决梯度消失的问题，大多数解释是在上述的更新公式下，递归导数（recursive derivative）的值等于1（原始的LSTM）或者值等于f（改进后的LSTM）。其中一个容易忘记的是，f、i和
都是关于
的函数，因此我们在计算梯度时必须将它们考虑在内。
都是关于的函数，因此我们在计算梯度时必须将它们考虑在内。接下来看看完整的LSTM的梯度。上面我们提到递归导数是造成梯度消失的主要原因，因此我们来解释一下完整的导数
。通过链式求导法则，我们可以得到
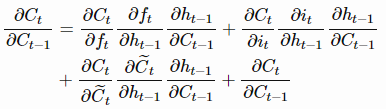
上述求导具体可以写为：
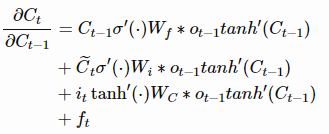
现在，如果我们要反向传播k个时间步，我们只要简单的将上述公式连乘k次就行。这与普通的RNN有很大的区别。对于普通的RNN，
的最终要么总是大于1，要么总是在[0, 1]范围内，这将导致梯度消失或者梯度爆炸。而对于LSTM，
在任何时间步，该值可以大于1，或者在[0, 1]范围内。因此，如果我们延伸到无穷的时间步，最终并不会收敛到0或者无穷。如果开始收敛到0，那么可以总是设置
的值（或者其他gate的值）更高一些，使得
的值接近1，从而防止了梯度消失（或者至少是，防止梯度不会那么快消失）。另外一个很重要的事情是，
的值是网络学习到的（根据当前的输入和隐藏层）。因此，在这种情况下，网络会学会决定什么时候让梯度消失，什么时候保持梯度，都可以通过设置gate的值来决定。
这看起来很神奇，但实际上如下两个原因：
- 为cell state的更新函数给出了一个更加“表现良好”的导数（ The additive update function for the cell state gives a derivative thats much more ‘well behaved’）
- 门控函数（gating function）允许网络决定梯度消失多少，并且可以在每个时间步长取不同的值。它们所取的值是从当前输入和隐藏状态学习到的。（ The gating functions allow the network to decide how much the gradient vanishes, and can take on different values at each time step. The values that they take on are learned functions of the current input and hidden state.）
以上就是LSTM解决梯度消失的本质。
附：
- recursive partial derivative 是一个雅可比矩阵（ Jacobian matrix）。
- 为了直观地理解递归权值矩阵的特征值的重要性，可以参考这篇文章。
- 对于LSTM的遗忘门（forget gate），递归导数仍然是许多0和1之间的数的和，然而在实践中，与RNN相比，这不是一个很大的问题。其中一个原因是我们的网络可以直接控制f的值。如果需要记住一些内容，网络可以很容易得将f取值高一点（如0.95左右）。因此，与tanh的导数值相比，这些值得收缩速度要慢的多。
- 为了完成完整的LSTM的推导，其实还有很多细节需要完成。本文不再赘述，感兴趣的可以参考这篇文章 PhD thesis of Alex Graves。
其他相关的文章链接：
RNN梯度消失和爆炸的原因 https://zhuanlan.zhihu.com/p/28687529
为什么相比于RNN，LSTM在梯度消失上表现更好？ https://www.zhihu.com/question/44895610
Why LSTMs Stop Your Gradients From Vanishing：A View from the Backwards Pass https://weberna.github.io/blog/2017/11/15/LSTM-Vanishing-Gradients.html
