机器学习中使用正则化来防止过拟合是什么原理?
什么是过拟合?在训练集上拟合非常好,在测试集上泛化非常差。另一种说法是, 当我们提高在训练数据上的表现时,在测试数据上反而下降。
过拟合现象有多种解释:
-
经典的是bias-variance decomposition ,但个人认为这种解释更加倾向于直观理解;
-
PAC-learning 泛化界解释, 这种解释是最透彻,最fundamental的;
-
Bayes先验解释,这种解释把正则变成先验, 在我看来等于没解释。
加入正则化是为了避免过拟合问题。
奥卡姆剃刀原理:如无必要,勿增实体。比如在机器学习领域,简单和复杂的模型都可以拟合数据,那么选择简单的那个模型。
L1正则化可以使得模型参数变得稀疏,L2正则化可以使得模型参数趋近于0。这可以使得模型变得简单(参数不那么极端),减少模型过拟合的风险。
“正则化削减了(容易过拟合的那部分)假设空间,从而降低过拟合风险”。
正则化其实就是对模型的参数设定一个先验,这是贝叶斯学派的观点,不过我觉得也可以一种理解。
L1正则是laplace先验,l2是高斯先验,分别由参数sigma确定。
L1正则化和L2正则化
L1正则化和L2正则化也被称为L1范数(l1-norm)和L2范数(l2-norm)
L1正则化和L2正则化可以看做是损失函数的惩罚项。所谓『惩罚』是指对损失函数中的某些参数做一些限制。对于线性回归模型,使用L1正则化的模型建叫做Lasso回归,使用L2正则化的模型叫做Ridge回归(岭回归)。
L1正则化是指权值向量w中各个元素的绝对值之和。
L2正则化是指权值向量w中各个元素的平方和然后再求平方根(可以看到Ridge回归的L2正则化项有平方符号)。
L1和L2的特点:
-
L1正则化可以产生稀疏权值矩阵,即产生一个稀疏模型,可以用于特征选择
-
L2正则化可以防止模型过拟合(overfitting);一定程度上,L1也可以防止过拟合
为什么L1会使得参数稀疏(参数值为0),为什么L2正则化会使得模型参数变得平滑?
角度1:L1正则化本身的导数性质
这个角度从权值的更新公式来看权值的收敛结果。
首先来看看L1和L2的梯度(导数的反方向):
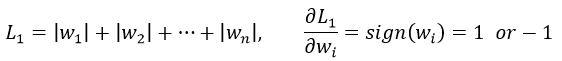
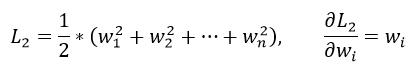
所以(不失一般性,我们假定:wi等于不为0的某个正的浮点数,学习速率η 为0.5):
L1的权值更新公式为wi = wi - η * 1 = wi - 0.5 * 1,也就是说权值每次更新都固定减少一个特定的值(比如0.5),那么经过若干次迭代之后,权值就有可能减少到0。
L2的权值更新公式为wi = wi - η * wi = wi - 0.5 * wi,也就是说权值每次都等于上一次的1/2,那么,虽然权值不断变小,但是因为每次都等于上一次的一半,所以很快会收敛到较小的值但不为0,所以会比较平滑。
此外,我们还可以得到,L2相对L1更稳定一些。
角度2:几何空间
假设我们的Loss函数是(y-wx)^2, 那么我们的几何解释如下图所示:
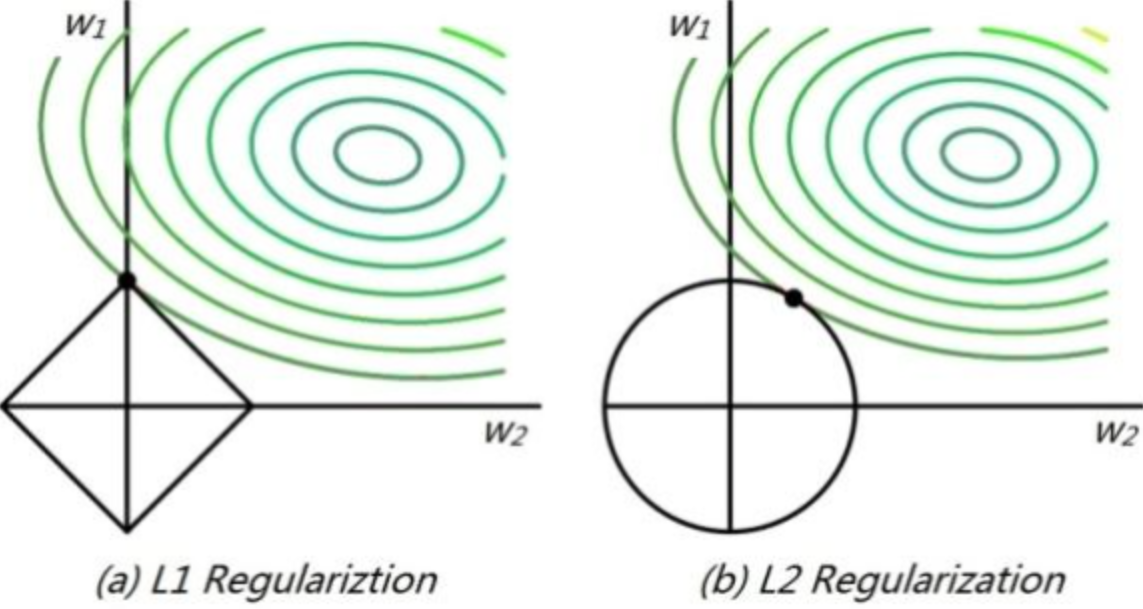
其中左图表示L1,右图表示L2。绿色代表的是loss的等高线,w1和w2 在L1中的取值空间如左图的菱形所示。在L2中的取值空间如右图的圆形所示。从等高线和取值空间的交点可以看到L1更容易倾向一个权重偏大一个权重为0。L2更容易倾向权重都较小。
为什么等高线是类似圆形?以linear regression举例,我们的目标函数E(w)=(y-wx)^2,可以看到E是关于w的平方函数,所以是类似圆形(椭圆形)。
为什么梯度下降的等值线与正则化函数第一次交点是最优解? 这是带约束的最优化问题,因为这里要用到拉格朗日乘子。参考:带约束的最优化问题(https://blog.csdn.net/NewThinker_wei/article/details/52857397)
参考链接:
机器学习中正则化项L1和L2的直观理解 https://blog.csdn.net/jinping_shi/article/details/52433975
为什么L1正则项产生稀疏的权重,L2正则项产生相对平滑的权重 https://blog.csdn.net/liangdong2014/article/details/79517638
L1正则化在0处不可导时怎么处理?
由于L1正则项在0处不可导,因此梯度下降法将不再有效。
方法1:坐标轴下降法
坐标轴下降法和梯度下降法具有同样的思想,都是沿着某个方向不断迭代,但是梯度下降法是沿着当前点的负梯度方向进行参数更新,而坐标轴下降法是沿着坐标轴的方向。 假设有m个特征个数,坐标轴下降法进参数更新的时候,先固定m-1个值,然后再求另外一个的局部最优解(EM思想),从而避免损失函数不可导问题。
算法过程如下:
- 给θ向量随机选取一个初值,记做θ0;
- 对于第k轮的迭代,从θ1k开始计算,θnk到为止,即先固定θ2k,θ3k,...,θnk,求取使得目标函数J最小的θ1k;然后固定θ1k,θ3k,...,θnk,求取使得目标函数J最小的θ2k;以此类推。
计算公式如下:
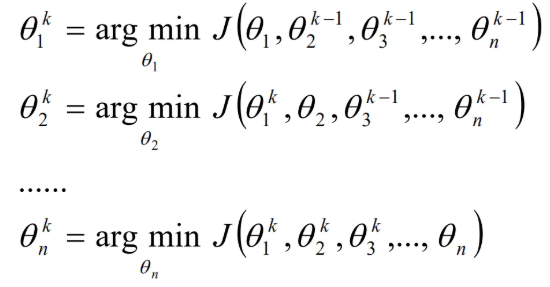
检查θk和θk-1向量在各个维度上的变化情况,如果所有维度的变化情况都比较小的话,那么认为结束迭代,否则继续k+1轮的迭代。
PS:在求解每个参数局部最优解的时候可以求导的方式来求解。
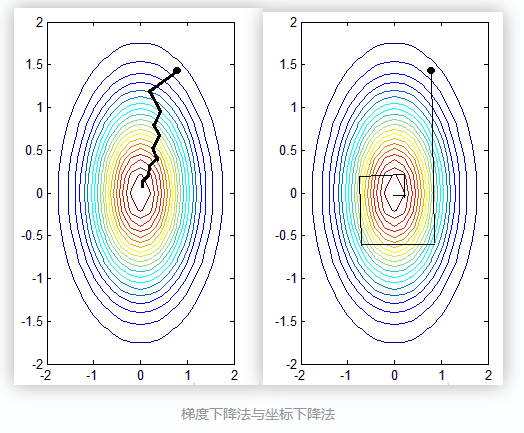
通过以上迭代过程可以看出
1. 坐标轴下降法进行参数更新时,每次总是固定另外m-1个值,求另外一个的局部最优值,这样也避免了Lasso回归的损失函数不可导的问题。
2. 坐标轴下降法每轮迭代都需要O(mn)的计算。(和梯度下降算法相同)
参考:
主题模型-坐标轴下降法 https://www.jianshu.com/p/6156764203de
方法2:Proximal Gradient Descent Algorithms 近端梯度下降
略


