从 SGD 到 Adam —— 常见优化算法总结

1 概览

虽然梯度下降优化算法越来越受欢迎，但通常作为黑盒优化器使用，因此很难对其优点和缺点的进行实际的解释。本文旨在让读者对不同的算法有直观的认识，以帮助读者使用这些算法。在本综述中，我们介绍梯度下降的不同变形形式，总结这些算法面临的挑战，介绍最常用的优化算法，回顾并行和分布式架构，以及调研用于优化梯度下降的其他的策略。

 

2 Gradient descent 变体

 

有3种基于梯度下降的方法，主要区别是我们在计算目标函数（ objective function）梯度时所使用的的数据量。

 

 

2.1 Batch gradient descent 批梯度下降法

 

计算公式如下：

 

 

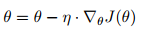
其中η表示学习率。

该方法在一次参数更新时，需要计算整个数据集的参数。

 

优点：可以保证在convex error surfaces 条件下取得全局最小值，在non-convex surfaces条件下取得局部极小值。

缺点：由于要计算整个数据集的梯度，因此计算比较慢，当数据量很大时，可能会造成内存不足。另外，该方法也无法在线（online）更新模型。

 

计算的伪代码如下：

for i in range ( nb_epochs ):
    params_grad = evaluate_gradient ( loss_function , data , params )
    params = params - learning_rate * params_grad

其中，params和params_grad均是向量（vector）。

2.2 Stochastic gradient descent（SGD） 随机梯度下降

计算公式如下：

随机梯度下降法每次更新参数时，只计算一个训练样本(x(i), y(i))的梯度。

 

优点：计算速度快，可以用于在线更新模型。

缺点：由于每次只根据一个样本进行计算梯度，因此最终目标函数收敛时曲线波动可能会比较大。 由于SGD的波动性，一方面，波动性使得SGD可以跳到新的和潜在更好的局部最优。另一方面，这使得最终收敛到特定最小值的过程变得复杂，因为SGD会一直持续波动。

然而，已经证明当我们缓慢减小学习率，SGD与批梯度下降法具有相同的收敛行为，对于非凸优化和凸优化，可以分别收敛到局部最小值和全局最小值。

 

 

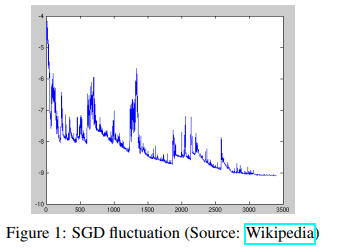
示例代码如下：

for i in range(nb_epochs):
    np.random.shuffle(data)
    for example in data:
        params_grad = evaluate_gradient(loss_function, example, params)
        params = params - learning_rate * params_grad

注：每次循环中，我们需要先将样本打乱。

 

2.3 Mini-batch gradient descent 

小批量梯度下降法结合了上述两种方法的优点，在每次跟新参数时使用小批量（n个样本）的训练样本。

 

 

优点：1）减少了参数更新时的方差，也就是目标函数收敛时的曲线波动没那么大了，这样也得到更加稳定的收敛结果。

          2）可以利用最新的深度学习库中高度优化的矩阵优化方法，高效地求解每个小批量数据的梯度。

 

小批量数据n的大小在50到256之间，也可以根据不同的应用有所变化。

当训练神经网络模型时，小批量梯度下降法是典型的选择算法，当使用小批量梯度下降法时，也将其称为SGD。

 

 

注意：在下文的改进的SGD中，为了简单，我们省略了参数。

 

示例代码如下：

for i in range(nb_epochs):
    np.random.shuffle(data)
    for batch in get_batches(data, batch_size=50):
        params_grad = evaluate_gradient(loss_function, batch, params)
        params = params - learning_rate * params_grad

3 Challenges

mini-batch梯度下降法虽然有上述的优点，但是仍然还是有一些问题：

1）选择一个合适的学习率比较困难。学习率太小会导致收敛缓慢，学习率太大会损失函数在最小值附近波动甚至无法收敛。

2）学习率调整（ Learning rate schedules）在训练时，根据预定义的策略（如目标函数的相邻迭代之间的下降值小于阈值时）减少学习率。这种方法需要提前设置好策略和阈值，而且可能无法适应数据集的特点。

3）所有参数的更新使用同一个学习率。如果我们的数据是稀疏的，同时特征的频率差异很大，我们可能不想使用同样的学习率更新所有的的参数，对于那些出现次数较少的特性，我们对其使用更大的学习率。

4）非凸误差函数普遍出现在神经网络中，在优化这类函数时，其中一个挑战就是使函数避免陷入次优的局部最小值。 Dauphin等人指出出现这种困难实际上并不是来自局部最小值，而是来自鞍点，即那些在一个维度上是递增的，而在另一个维度上是递减的。这些鞍点通常被具有相同误差的点包围，因为在任意维度上的梯度都近似为0，所以SGD很难从这些鞍点中逃开。

 

 

 

4 Gradient descent optimization algorithms

    下面我们将介绍一些在深度学习中广泛使用的优化算法，来解决上述提到的问题。我们不会讨论实际中不适合高维数据集中计算的算法，如牛顿法的二阶方法。

 

 

4.1 Momentum 动量法

 

    动量法改进自SGD算法，让每一次的参数更新方向不仅仅取决于当前位置的梯度，还受到上一次参数更新方向的影响。

 

SGD很难通过陡谷（指在一个维度上的表面弯曲程度远大于其他维度的区域），这种情况通常出现在局部最优点附近。 在这种情况下，SGD摇摆地通过陡谷的斜坡，同时，沿着底部到局部最优点的路径上只是缓慢地前进，这个过程如图2a所示。

 

 

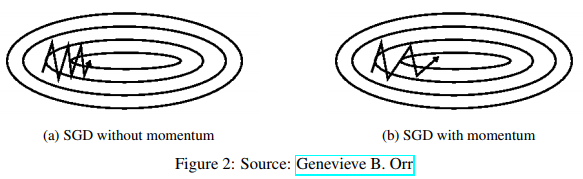
如图2b所示，动量法[16]是一种帮助SGD在相关方向上加速并抑制摇摆的一种方法。动量法将历史步长的更新向量的一个分量增加到当前的更新向量中（部分实现中交换了公式中的符号）

 

公式如下：

 

其中，动量项γ一般取值为0.9或者类似的值。

 

从本质上说，动量法，就像我们从山上推下一个球，球在滚下来的过程中累积动量，变得越来越快（直到达到终极速度，如果有空气阻力的存在，则γ<1）。同样的事情也发生在参数的更新过程中：对于在梯度点处具有相同的方向的维度，其动量项增大，对于在梯度点处改变方向的维度，其动量项减小。因此，我们可以得到更快的收敛速度，同时可以减少摇摆。

 

4.2 Nesterov accelerated gradient (NAG)

 

NAG是在Momentum的基础上改进的。 NAG就对Momentum说：“既然我都知道我这一次一定会走的量，那么我何必还用现在这个位置的梯度呢？我直接先走到之后的地方，然后再根据那里的梯度再前进一下，岂不美哉？”所以就有了下面的公式：

跟上面Momentum公式的唯一区别在于，梯度不是根据当前参数位置θ，而是根据先走了本来计划要走的一步后，达到的参数位置计算出来的。

 

对于这个改动，很多文章给出的解释是，能够让算法提前看到前方的地形梯度，如果前面的梯度比当前位置的梯度大，那我就可以把步子迈得比原来大一些，如果前面的梯度比现在的梯度小，那我就可以把步子迈得小一些。这个大一些、小一些，都是相对于原来不看前方梯度、只看当前位置梯度的情况来说的。

但是我个人对这个解释不甚满意。你说你可以提前看到，但是我下次到了那里之后不也照样看到了吗？最多比你落后一次迭代的时间，真的会造成非常大的差别？可是实验结果就是表明，NAG收敛的速度比Momentum要快。 

对NAG原来的更新公式进行变换，得到的等效形式如下：

 

注：上述公式对应的原公式为：

 

这个NAG的等效形式与Momentum的区别在于，本次更新方向多加了一个，它的直观含义就很明显了：如果这次的梯度比上次的梯度变大了，那么有理由相信它会继续变大下去，那我就把预计要增大的部分提前加进来；如果相比上次变小了，也是类似的情况。这样的解释听起来好像和原本的解释一样玄，但是读者可能已经发现了，这个多加上去的项不就是在近似目标函数的二阶导嘛！所以NAG本质上是多考虑了目标函数的二阶导信息，怪不得可以加速收敛了！其实所谓“往前看”的说法，在牛顿法这样的二阶方法中也是经常提到的，比喻起来是说“往前看”，数学本质上则是利用了目标函数的二阶导信息。

 

分析详见：https://zhuanlan.zhihu.com/p/22810533/

 

既然我们能够使得我们的更新适应误差函数的斜率以相应地加速SGD，我们同样也想要使得我们的更新能够适应每一个单独参数，以根据每个参数的重要性决定大的或者小的更新。

 

4.3 Adagrad

Adagrad是这样一种基于梯度的优化算法：它让学习率适应参数，对于出现次数较少的特征，我们对其采用更大的学习率，对于出现次数较多的特征，我们对其采用较小的学习率。因此，Adagrad非常适合处理稀疏数据。

AdaGrad算法就是将每一个参数的每一次迭代的梯度取平方累加后在开方，用全局学习率除以这个数，作为学习率的动态更新。

 

具体的计算方法如下：

1）计算梯度

2）累计平方梯度

3）计算更新

注：上述计算方法为：逐元素地应用除法和求平方根

 

4）应用更新

 

其中，G为梯度累积变量（是一个d*d的对角矩阵，矩阵中第(i,i)的元素为第i个参数的平方和），ε是一个小的常数，避免分母为0。

 

简版迭代公式如下：

 

 

经验上已经发现，对于训练深度神经网络模型而言，从训练开始时积累梯度平方会导致有效学习率过早和过量的减小。Adagrad在某些深度学习模型上效果不错，但不是全部。

 

Adagrad的其中一个优点就是不需要手动的调整学习率，一般默认使用0.01作为初始学习率。

Adagrad的一个主要缺点是它在分母中累加梯度的平方：由于没增加一个正项，在整个训练过程中，累加的和会持续增长。这会导致学习率变小以至于最终变得无限小，在学习率无限小时，Adagrad算法将无法取得额外的信息。接下来的算法旨在解决这个不足。

 

4.4 Adadelta

 

Adadelta是Adagrad的一种扩展算法，以处理Adagrad学习速率单调递减的问题。不是计算所有的梯度平方，Adadelta将计算计算历史梯度的窗口大小限制为一个固定值。

 

在Adadelta中，无需存储先前的w个平方梯度，而是将梯度的平方递归地表示成所有历史梯度平方的均值。在t时刻的均值只取决于先前的均值和当前的梯度（分量类似于动量项）：

一般γ取0.9。

我们将adagrad中的G替换为，则有

上述分母相当于梯度的均方根（root mean aquared， RMS），因此可以用RMS简写

 

作者指出上述更新公式中的每个部分（与SGD，动量法或者Adagrad）并不一致，即更新规则中必须与参数具有相同的假设单位。为了实现这个要求，作者首次定义了另一个指数衰减均值，这次不是梯度平方，而是参数的平方的更新：

 

 

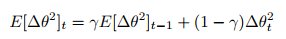
因此，参数更新的均方根误差为：

 

由于是未知的，我们利用参数的均方根误差来近似更新。利用替换先前的更新规则中的学习率，最终得到Adadelta的更新规则：

 

算法最终实现如下：

 

 

使用Adadelta算法，我们甚至都无需设置默认的学习率，因为更新规则中已经移除了学习率。

 

4.5 RMSprop

 

RMSprop是一个未被发表的自适应学习率的算法，该算法由Geoff Hinton在其Coursera课堂的课程6e中提出。

RMSprop和Adadelta在相同的时间里被独立的提出，都起源于对Adagrad的极速递减的学习率问题的求解。实际上，RMSprop是先前我们得到的Adadelta的第一个更新向量的特例：

 

 

 

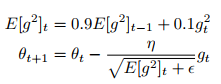
同样，RMSprop将学习率分解成一个平方梯度的指数衰减的平均。Hinton建议将γ设置为0.9，对于学习率，一个好的固定值为0.001。

 

4.6 Adam

 

 

自适应矩估计（Adaptive Moment Estimation，Adam）[9]是另一种自适应学习率的算法，Adam对每一个参数都计算自适应的学习率。除了像Adadelta和RMSprop一样存储一个指数衰减的历史平方梯度的平均，Adam同时还保存一个历史梯度的指数衰减均值，类似于动量：

 

 

和分别是对梯度的一阶矩（均值）和二阶矩（非确定的方差）的估计，正如该算法的名称。当​和​初始化为0向量时，Adam的作者发现它们都偏向于0，尤其是在初始化的步骤和当衰减率很小的时候（例如β1和β2趋向于1）。

 

通过计算偏差校正的一阶矩和二阶矩估计来抵消偏差

正如我们在Adadelta和RMSprop中看到的那样，他们利用上述的公式更新参数，由此生成了Adam的更新规则：

 

作者建议β1取默认值为0.9，β2为0.999，ε​为1e-8。他们从经验上表明Adam在实际中表现很好，同时，与其他的自适应学习算法相比，其更有优势。

 

4.7 AdaMax

 

见原文

 

4.8 Nadam

 

见原文

 

 

 

 

4.9 Visualization of algorithms

下面两张图给出了上述优化算法的优化行为的直观理解。（还可以看看这里关于Karpathy对相同的图片的描述以及另一个简明关于算法讨论的概述）。

在图4a中，我们看到不同算法在损失曲面的等高线上走的不同路线。所有的算法都是从同一个点出发并选择不同路径到达最优点。注意：Adagrad，Adadelta和RMSprop能够立即转移到正确的移动方向上并以类似的速度收敛，而动量法和NAG会导致偏离，想像一下球从山上滚下的画面。然而，NAG能够在偏离之后快速修正其路线，因为NAG通过对最优点的预见增强其响应能力。

图4b中展示了不同算法在鞍点出的行为，鞍点即为一个点在一个维度上的斜率为正，而在其他维度上的斜率为负，正如我们前面提及的，鞍点对SGD的训练造成很大困难。这里注意，SGD，动量法和NAG在鞍点处很难打破对称性，尽管后面两个算法最终设法逃离了鞍点。而Adagrad，RMSprop和Adadelta能够快速想着梯度为负的方向移动，其中Adadelta走在最前面。

 

              

 

 

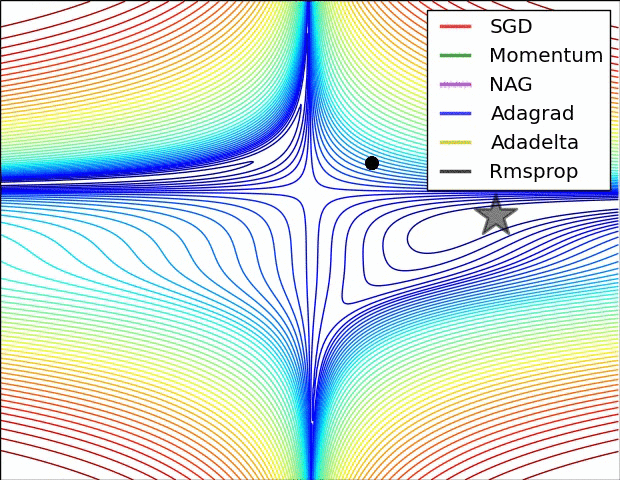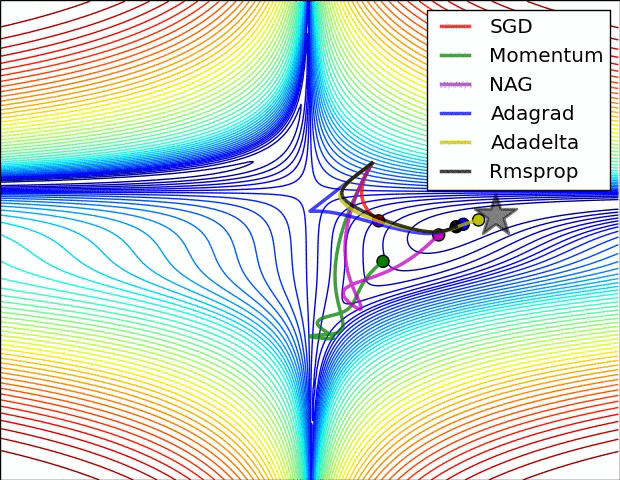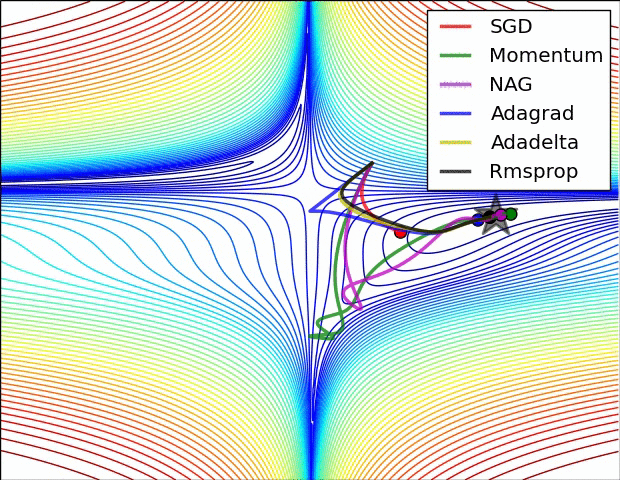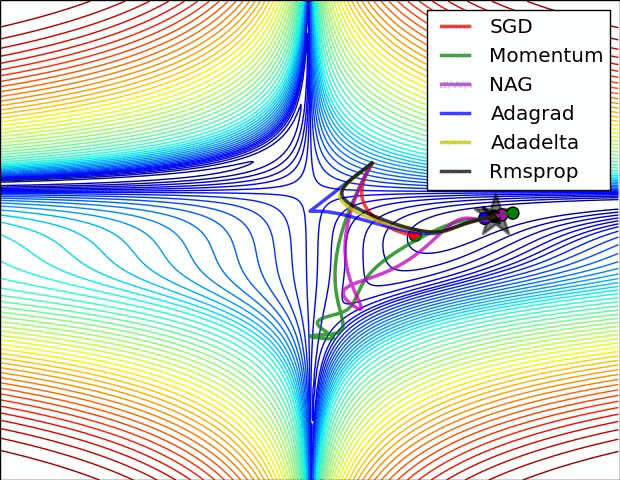
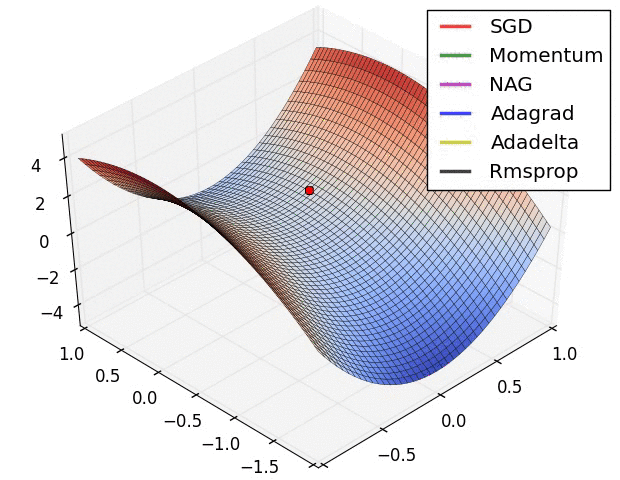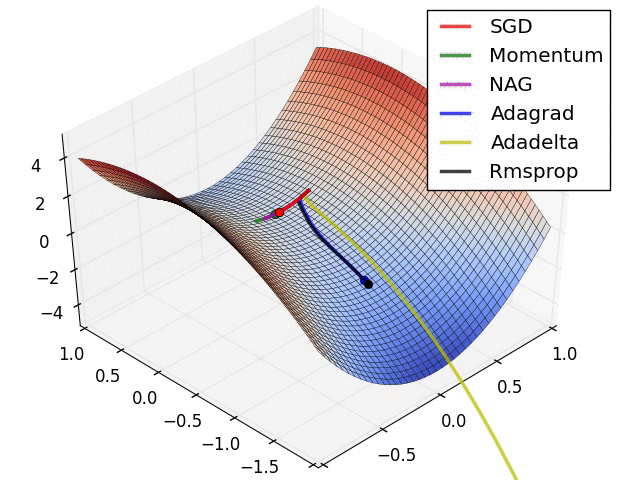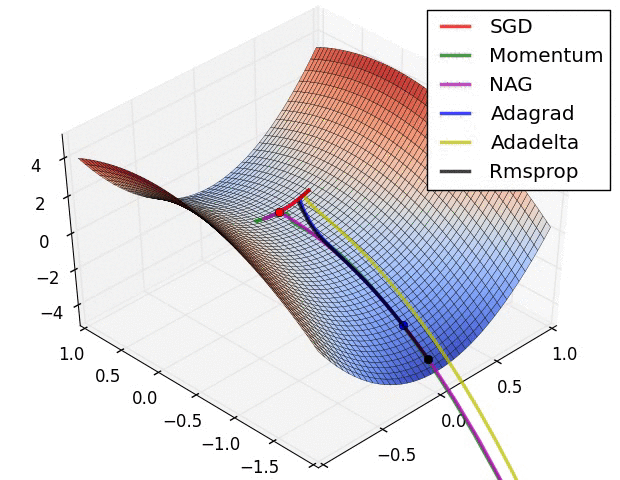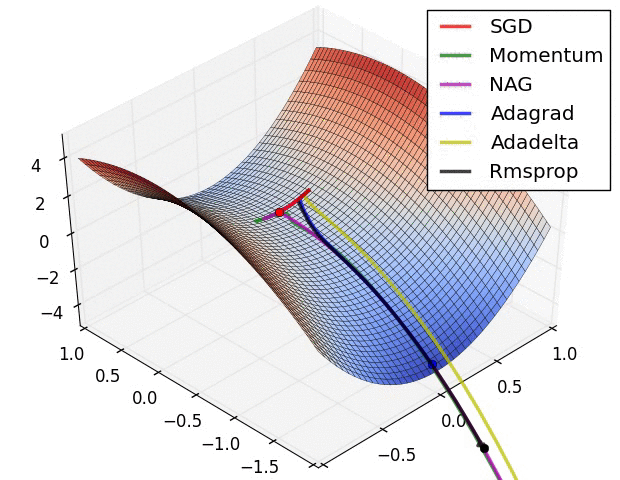
正如我们所看到的，自适应学习速率的方法，即 Adagrad、 Adadelta、 RMSprop 和Adam，最适合这些场景下最合适，并在这些场景下得到最好的收敛性。

 

4.10 Which optimizer to use?

 

那么，我们应该选择使用哪种优化算法呢？如果输入数据是稀疏的，选择任一自适应学习率算法可能会得到最好的结果。选用这类算法的另一个好处是无需调整学习率，选用默认值就可能达到最好的结果。

 

总的来说，RMSprop是Adagrad的扩展形式，用于处理在Adagrad中急速递减的学习率。RMSprop与Adadelta相同，所不同的是Adadelta在更新规则中使用参数的均方根进行更新。最后，Adam是将偏差校正和动量加入到RMSprop中。在这样的情况下，RMSprop、Adadelta和Adam是很相似的算法并且在相似的环境中性能都不错。Kingma等人[9]指出在优化后期由于梯度变得越来越稀疏，偏差校正能够帮助Adam微弱地胜过RMSprop。综合看来，Adam可能是最佳的选择。

有趣的是，最近许多论文中采用不带动量的SGD和一种简单的学习率的退火策略。已表明，通常SGD能够找到最小值点，但是比其他优化的SGD花费更多的时间，与其他算法相比，SGD更加依赖鲁棒的初始化和退火策略，同时，SGD可能会陷入鞍点，而不是局部极小值点。因此，如果你关心的是快速收敛和训练一个深层的或者复杂的神经网络，你应该选择一个自适应学习率的方法。

 

 

参考：

博客原文： https://ruder.io/optimizing-gradient-descent/

An overview of gradient descent optimization algorithms

https://blog.csdn.net/qq_16234613/article/details/78912322

Nesterov accelerated gradient 深入理解：https://zhuanlan.zhihu.com/p/22810533/

https://cs231n.github.io/neural-networks-3/#sgd

深度学习优化方法-AdaGrad https://blog.csdn.net/program_developer/article/details/80756008