相似度计算方法

1.余弦相似度

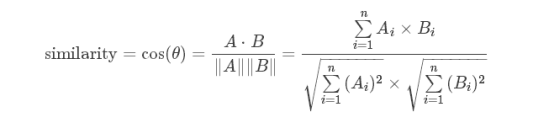
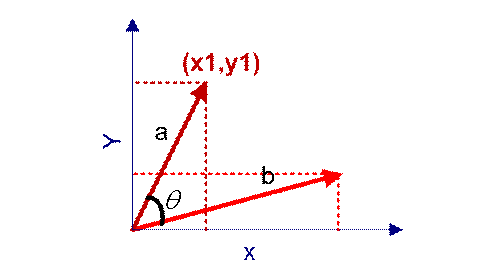
在平面系 a向量与b向量的夹角越小，说明相似度越大，余弦值越接近1，就表明夹角越接近0度，也就是两个向量越相似，这就叫"余弦相似性"。

在三维也是一个道理（x,y,z）确定的一点与点（a,b,c）一点的夹角

高中学过向量a与向量b的乘积定义为：

所以两者的夹角为 cos=a*b/|a|*|b|

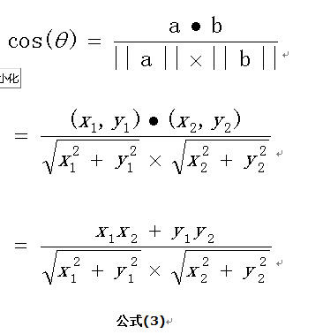
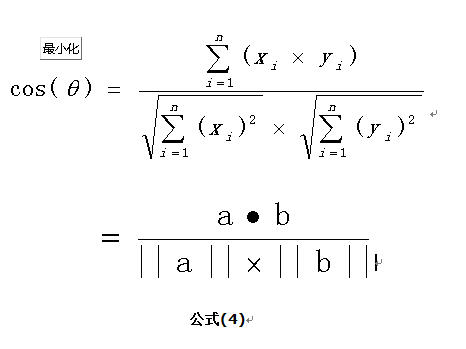
分子代表：集合n个(x*y)之和

分母：所有集合n个x^2之和开方+n个y^2之和开方  代表向量a集合n维的模

对于多维的也是一样的

集合A：(1，1，2，1，1，1，0，0，0)

集合B：(1，1，1，0，1，1，1，1，1)

 

2.欧氏距离：

 

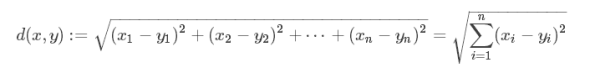
就是计算空间上两点间的距离。下图很好体现了欧氏距离和余弦相似度的差异。

所以可以看出 欧氏距离 适用于 那些 对数值差异大小敏感的 相似度计算，

而 余弦相似度 更适用于 判别方向上的差异，而对绝对的数值不敏感的，比如 通过用户对 内容的评分来区分兴趣的相似度，修正了不同用户之间可能存在度量标准不统一的问题（有的用户默认高分，有的用户默认低分，对于默认低分用户来说7分就表示他喜欢了，而对默认高分用户来说10分才表示喜欢）。