深度优先搜索和广度优先搜索
深度优先搜索(DFS)和广度优先搜索(BFS)是图的两种遍历方式。
举个例子，如果我们需要遍历下面这张图的全部节点，有两种选择：
1.选择其中一个节点，一直往前遍历，直至走到死胡同再往后退一步，如果有其他路的话就换条路继续往前走(没路就只能再往后退一步)，直至遍历完所有节点。这就是DFS，显然这种方式蕴含了递归+回溯的思想。
2.选择其中一个节点，先遍历与其相邻的所有节点，记为节点集合A，然后遍历与集合A相邻的所有节点记为集合B，以此类推。这就是BFS，显然其蕴含了迭代的思想。
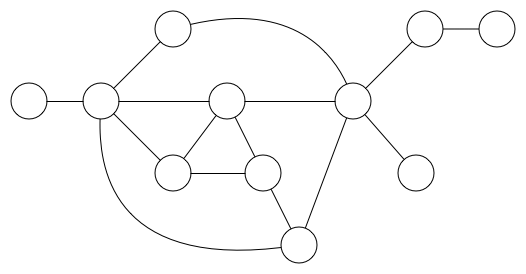
我想从几道算法题来说明一下这两种算法。
一.深度优先搜索
问题一：给定一个包含了一些 0 和 1 的非空二维数组 grid 。
一个岛屿是由一些相邻的1(代表土地)构成的组合，这里的「相邻」要求两个1必须在水平或者竖直方向上相邻。
你可以假设 grid 的四个边缘都被 0（代表水）包围着。找到给定的二维数组中最大的岛屿面积。(如果没有岛屿，则返回面积为0。)
[[0,0,1,0,0,0,0,1,0,0,0,0,0], [0,0,0,0,0,0,0,1,1,1,0,0,0], [0,1,1,0,1,0,0,0,0,0,0,0,0], [0,1,0,0,1,1,0,0,1,0,1,0,0], [0,1,0,0,1,1,0,0,1,1,1,0,0], [0,0,0,0,0,0,0,0,0,0,1,0,0], [0,0,0,0,0,0,0,1,1,1,0,0,0], [0,0,0,0,0,0,0,1,1,0,0,0,0]] 结果为6
这是leetcode上一道经典的DFS问题，难度中等，类似问题岛屿数量思路基本一致。
思路就是对每一个岛屿求面积，输出最大值。而求岛屿面积的方式就是深度优先搜索，从其中的一个1入手通过递归的方式寻找与其相邻的1来得到岛屿的面积，递归终止于某个 附近没有未遍历的1的 1，比如我们从grid[0][7]入手，将终止于grid[1][9]。我们一起来看一下代码(Python)：
def maxAreaOfIsland(grid): def dfs(x, y, grid):
#递归终止条件 if grid[x][y] == 0: return 0
#面积初值为1 val = 1 grid[x][y] = 0 #访问过的1记为0 d = [(1,0),(-1,0),(0,1),(0,-1)] #上下左右四个方向 for dx,dy in d: if 0<=x+dx<=len(grid)-1 and 0<=y+dy<=len(grid[0])-1: val += dfs(x+dx, y+dy, grid) #面积累积 return val res = 0 for i in range(len(grid)): for j in range(len(grid[0])): res = max(res, dfs(i, j, grid)) return res
代码整体思路应该是比较清晰的，相关说明在注释中有所展现。
上述代码还有一些优化空间，比如在遍历grid的时候，无需将每个元素都调用dfs函数，只需对值1执行即可(当然，dfs函数也要做相应修改)。这样是为了将递归的终止条件更清晰地展现出来，即grid[x][y]==0。
实际上，我们运用DFS最多的地方可能是树的相关问题，因为树的特点完美契合DFS算法，我们也会发现DFS算法解决树的问题会让代码更清晰、更简单，比如下面这个问题。
问题二：输入一棵二叉树的根节点，判断该树是不是平衡二叉树。 如果某二叉树中任意节点的左右子树的深度相差不超过1，那么它就是一棵平衡二叉树。 给定二叉树 [3,9,20,null,null,15,7] 3 / \ 9 20 / \ 15 7 返回 true 。
在不了解DFS算法的情况下，这个问题将变得无从下手，如果采用层次遍历(实际上就是BFS)的方式，这个问题的复杂度很高，而且代码也很难写。但是用DFS思路就简单多了，这个题无非就是在求每个节点的左右子树的深度，从根节点到叶子节点依次加1即可。
def isBalanced(root): def dfs(root): if not root: return 0 lt = dfs(root.left) rt = dfs(root.right) if lt == -1 or rt == -1 or abs(lt-rt) > 1: return -1 return max(lt, rt) + 1 return dfs(root) != -1
这里有个小技巧，就是用-1作为返回值起到一个标志位的作用，这样可以避免设置一个全局变量。我们这里用到了一个内部函数dfs，如果设置一个全局变量的话是只能引用而无法改变其值的。当然如果是在leetcode上刷题，我们编写的是一个Solution类，那就可以设置类变量来作为标志，即self.flag = True这样。
运用DFS解决问题最重要的就是一点：我们写的这个DFS函数到底要做什么。这是我认为是这类问题的下手点，也是最大的难点。很多同学读完问题能隐约感觉的到要用DFS，但是不知道DFS函数如何写，包括终止条件、函数逻辑和参数列表都无从下手，在我看来就是没抓住一个核心的问题：要写的DFS函数的功能是什么。比如第一题中DFS做的事情就是要求grid中每个元素所在的岛屿面积，那么函数逻辑就是求上下左右的各个元素所在的岛屿面积并将访问过的1变为0，终止条件就是当前元素值为0，参数列表就是元素的坐标和grid(因为我们要维护一个不断更新的grid，1→0)，这样就很清晰了。
二.广度优先搜索
接下来我们再看看BFS。由于BFS比较好理解，我们直接来看看最经典的层次遍历二叉树：
从上到下打印出二叉树的每个节点，同一层的节点按照从左到右的顺序打印。 例如: 给定二叉树: [3,9,20,null,null,15,7] 3 / \ 9 20 / \ 15 7 返回：[3,9,20,15,7]
这个问题显然使用BFS的方式会简单很多，我们看一下BFS标准的代码是怎么写的：
def levelOrder(root): if not root: return [] queue = [root] res = [] while queue: temp = [] for i in queue: res.append(i.val) if i.left: temp.append(i.left) if i.right: temp.append(i.right) queue = temp return res
这样的遍历方式很符合我们一般的思维方式，一层一层的来就可以。首先用根节点来初始化一个队列，然后对这个队列进行迭代，迭代的方式就是依次地将左右子节点放入队列中(如果存在的话)，遍历完当前队列之后更新一次(长江后浪推前浪)，前浪是当前队列queue，后浪我们借助一个临时队列temp。循环终止于队列为空，此时迭代结束返回结果。
当然，很多问题都是DFS与BFS都可以解决(可以说只要其中一种方法行，那另外一种方法肯定也行，无非就是复杂程度不同)。我们来对比一下同一个问题用两种方式的区别：
给定一个二叉树，找出其最小深度。最小深度是从根节点到最近叶子节点的最短路径上的节点数量。 输入：root = [3,9,20,null,null,15,7]
3
/ \
9 20
/ \
15 7
输出：2
这个问题其实初学者很容易看到求树的深度就立马往DFS的方向思考，于是写出下面的代码：
def minDepth(root): if not root: return 0 if not root.left: return minDepth(root.right) + 1 if not root.right: return minDepth(root.left) + 1 return min(minDepth(root.left), minDepth(root.right)) + 1
DFS其实就是计算出了根到所有叶节点的路径长度取最小值，但是我们考虑一种情况，如果根节点的左子树很长，而右子树很短，那么右子树的高度以后的计算就都是多余的了。在示例中，当我们发现9是叶子节点就可以直接返回结果了，也就是说这个问题无需遍历全部节点：
def minDepth(root): res = 0 if not root: return 0 queue = [root] while queue: temp = [] res += 1 for i in queue: if not i.left and not i.right: return res if i.left: temp.append(i.left) if i.right: temp.append(i.right) queue = temp
与上一题的思路一致，结果返回于找到某一节点为叶子节点，无需遍历节点。
有关树和图的问题思路基本上就是DFS或者BFS，在方法选择时，我们可以根据具体问题的要求，模拟解决问题的流程，这样就可以比较DFS和BFS哪个更合适了。
