PCA
PCA
如果1,二维数据,在维空间可以通过不同的正交坐标系表示,数据在坐标系上的方差可以表示数据的信息量。要完成降维工作,需要信息方差最大的坐标系。如图2,保留主元1坐标系。

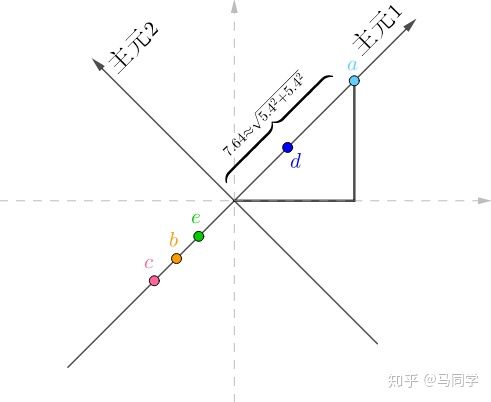
同一点在不同坐标系的转换可以通过矩阵运算实现。如下所示:
\[\bigl(\begin{smallmatrix}
1/\sqrt{2}& 1/\sqrt{2}\\ -1/\sqrt{2}
& 1/\sqrt{2}
\end{smallmatrix}\bigr)*\begin{pmatrix}
3\\2
\end{pmatrix}=\begin{pmatrix}
5/\sqrt{2}\\ -1/\sqrt{2}
\end{pmatrix}
\]
将一组N维向量降为K维(K大于0,小于N),目标是是选择K个单位正交基,使原始数据变换到这组基上后,各字段两两协方差为0,字段的方差则尽可能大。




