STL的集合set

集合：

集合是由元素组成的一个类，其成员可以是一个集合，也可以是一个原子，通常一个元素在一个集合中不能多次出现；由于对实现集合不是很理解，只简单写下已有的STL中的set集合使用；

C++中set基本运算及操作：

begin():返回指向第一个元素的迭代器

clear()：清除所有元素；

empty():判断集合是否为空，若为空，返回true；

end()：返回指向最后一个元素的迭代器；

size():返回集合中元素的数目；

lower_bound():返回指向大等于某值的第一个元素的迭代器；

set_union():合并两个集合；

set_intersection():两个集合的交集；

set_difference()：前面集合对后面集合的差集；

合并集合：

调用代码：

#include<cstdio>
#include<cstdlib>
#include<algorithm>
#include<iostream>
#include<set>
using namespace std;
struct Stu
{
	int ID;
	int val;
};
struct cmp
{
	bool operator()(const Stu& t1, const Stu& t2)
	{
		if (t1.val<t2.val)return true;
		else if (t1.val == t2.val)
		{
			if (t1.ID<t2.ID)return true;
		}
		else return false;
	}
};
int main()
{
	set<Stu, cmp>s1;
	set<int>s2;
	set<int>s3;
	set<int>uni;
	set<int>inter;
	set<int>dif;
	Stu stu1, stu2, stu3;
	stu1.val = 80; stu2.val = 85; stu3.val = 85;
	stu1.ID = 31602114; stu2.ID = 31602113; stu3.ID = 31602115;
	s1.insert(stu1); s1.insert(stu2); s1.insert(stu3);
	s2.insert(10); s2.insert(13); s2.insert(54); s2.insert(7);
	s3.insert(1);s3.insert(12);s3.insert(54);s3.insert(13);
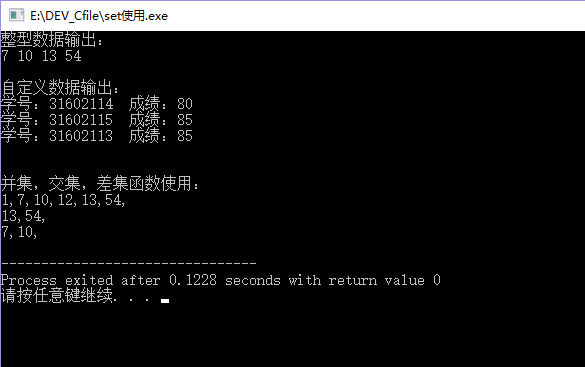
	printf("整型数据输出：\n");
	set<int>::iterator int_iter;
	set<Stu, cmp>::iterator Stu_iter;
	for (int_iter = s2.begin(); int_iter != s2.end(); int_iter++)
		printf("%d ", *int_iter);
	printf("\n\n");
	printf("自定义数据输出：\n");
	for (Stu_iter = s1.begin(); Stu_iter != s1.end(); Stu_iter++)
		printf("学号：%d  成绩：%d\n", Stu_iter->ID, Stu_iter->val);
	printf("\n\n");
	printf("并集，交集，差集函数使用：\n"); 
	set<int>::iterator s;
	set_union(s2.begin(),s2.end(),s3.begin(),s3.end(),inserter(uni,uni.begin()));                            //s2与s3的并集 ,放入到uni中了 ； 
	set_intersection(s2.begin(),s2.end(),s3.begin(),s3.end(),inserter(inter,inter.begin()));                 //s2与s3的交集 ，放入到inter中了； 
	set_difference(s2.begin(),s2.end(),s3.begin(),s3.end(),inserter(dif,dif.begin()));                       //s2对s3的差集 ，放入到dif中了； 
	for(s=uni.begin();s!=uni.end();s++)
		printf("%d,",*s);
	printf("\n");
	for(s=inter.begin();s!=inter.end();s++)
		printf("%d,",*s);
	printf("\n");
	for(s=dif.begin();s!=dif.end();s++)
		printf("%d,",*s);
	printf("\n"); 
	
	return 0;
}

这里讲到lower_bound就简要写一下lower_bound的使用：假设存在一个数组num[]：5,16,19,75,94,101；位置变量pos;

pos=lower_bound(num,num+6,15);

即pos返回的是第一个比15大等的元素的位置，此时pos=1；

pos=lower_bound(num,num+6,110);

pos是返回第一个比110大等的元素的位置，若不存在，则返回最右端元素的下一位下标，即size;此时pos=6；

lower_bound的核心思想：使用二分法对元素进行查找；

大致实现源代码：

//这个算法中，first是最终要返回的位置
int lower_bound(int *array, int size, int key)
{
    int first = 0, middle;
    int half, len;
    len = size;

    while(len > 0) {
        half = len >> 1;
        middle = first + half;
        if(array[middle] < key) {     
            first = middle + 1;          
            len = len-half-1;       //在右边子序列中查找
        }
        else
            len = half;            //在左边子序列（包含middle）中查找
    }
    return first;
}

还有需要自己实现的集合代码没有学习，之后有空再补上吧；