树的实现及应用
树
树是由一个集合及在该集合上定义的一种层次关系构成的。几个树中的名词:
度:
一个节点的儿子节点个数称为该节点的度,一棵树的度是指该树中节点的最大度数。
叶节点:
树中度为0的节点称为叶节点(终端节点);
内部节点:
树中除根节点的且度不为0的节点称为内部节点;
路径:
如果存在树中的一个节点序列k1,k2,...kj,使得节点ki是ki+1的父节点(1<=i<j),则称该节点序列是树中从节点ki到节点kj的一条路径;
高度:
树的一个节点的高度是指从该节点到各叶节点的最长路径的长度;
深度:
从树根到任一节点n有唯一的一条路径,称这条路径的长度为节点n的深度或层次;
树的遍历:
如图假设为一棵树,其中T1,T2可看成是子树(不一定只有一个节点)
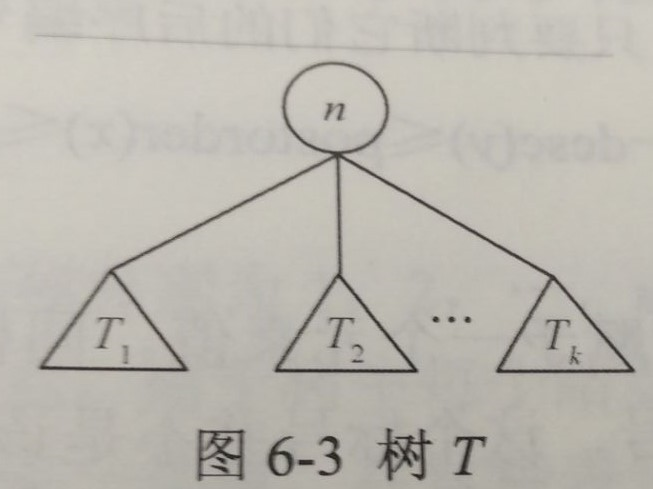
树的遍历就是将树中的每个节点访问一次且仅访问一次;一般有三种遍历方式:
前序遍历:
先访问树根n,然后依次前序遍历T1,T2,T3...,Tk;
中序遍历:
先中序遍历T1,然后访问树根n,接着对T2,T3,Tk进行中序遍历;(如果T2这些不是单个节点,则遍历方式就是一个类似的过程,对以T2为根节点的子树中序遍历)
后序遍历:
先一次对T1,T2,T3,...,Tk进行后序遍历,最后访问树根n;
遍历图解: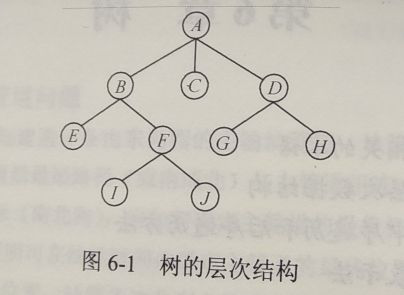
通过三种遍历方式遍历上图列表:
前序:A B E F I J C D G H
中序:E B I F J A C G D H
后序:E I J F B C G H D A
思路:在对每一个节点遍历,都是对将其作为根节点的子树进行遍历;
树的表示:
父节点数组表示法:开辟一个fa[]数组,从1到n的编号代表每个节点的编号,其中保存的值就是这个节点的父亲节点编号;
儿子链表示法:每个节点建立一个节点表,各节点的儿子表表头存放于数组header中;
二叉树:
二叉树中每个节点至多有两个儿子,并且有左、右之分,任一节点要么没有儿子,要么只有左儿子,要么只有右儿子,要么有一个左儿子和一个右儿子这四种情况;
二叉树的性质:
1、高度h>=0的二叉树至少有h+1个节点;
2、高度不超过h的二叉树至多有2^(h+1)-1个节点;
3、含有n>=1个节点的二叉树的高度至多为n-1,至少为logn;
典型问题:
具有n个节点的不同二叉树的数目有多少?二叉树是递归定义的,因此易知其递归方程是
Bn=1; n=0;
Bn=Sum(Bi*Bn-i-1) (i=0,1,2,3,...n-1) n>=1;
Bn的通解是Bn=C(2n,n)/(n+1),也就是常见的Catalan数;
Catalan数参考博客:http://blog.csdn.net/mobius_strip/article/details/39229895
满二叉树及近似满二叉树:
满二叉树:
每一层上的节点数都达到最大值;
近似满二叉树:
二叉树中至多只有最下面的两层上节点的度数可以小于2,并且最下面一层的节点都集中在最左边,称之为近似满二叉树;
图析:
二叉树的指针实现代码:
#include<cstdio>
#include<cstdlib>
#include<algorithm>
#include<malloc.h>
typedef struct node* link;
typedef struct node
{
link parent;
int element;
link lchild;
link rchild;
}Node;
//typedef struct atree* Tree;
//typedef struct atree
//{
// link root;
//}Atree;
void print_sorted_tree(link tr) //中序遍历输出树 ;
{
if(tr==NULL)return;
print_sorted_tree(tr->lchild);
printf("%d \n",tr->element);
print_sorted_tree(tr->rchild);
}
link find_min(link tr) //寻找tr为根节点的树中的最小值;
{
link np=tr;
if(np==NULL)return NULL;
while(np->lchild!=NULL)
{
np=np->lchild;
}
return np;
}
link find_max(link tr) //寻找tr为根节点的树中的最大值 ;
{
link np=tr;
if(np==NULL)return NULL;
while(np->rchild!=NULL)
{
np=np->rchild; //根据二叉树的定义,右儿子一定比其大,则每次都往右边找值;
}
return np;
}
link find_value(link tr,int value) //寻找树中是否有value这个值,如果有则,输出其位置(link),否则输出NULL;
{
if(tr==NULL)return NULL;
if(tr->element==value)return tr;
else if(value<tr->element)return find_value(tr->lchild,value);
else return find_value(tr->rchild,value);
}
int is_root(link np) //判断np节点是否是根节点;
{
return (np->parent==NULL);
}
int is_leaf(link np) //判断np节点是否是叶节点;
{
return (np->lchild==NULL&&np->rchild==NULL);
}
int delete_leaf(link np) //np是叶节点时,删除叶节点;
{
int element;
link parent;
element=np->element;
parent=np->parent;
if(!is_root(np)) //直接将np的父节点的左或右儿子置为NULL即可;
{
if(parent->lchild==np)
{
parent->lchild=NULL;
}
else parent->rchild=NULL;
}
free(np); //将np释放;
return element;
}
int delete_node(link np) //删除某个节点,里面还需要判断其是否是叶节点跳转到叶节点删除函数;
{
link replace;
int element;
if(is_leaf(np))return delete_leaf(np);
else
{
replace=(np->lchild!=NULL)?find_max(np->lchild):find_min(np->rchild); //此时np有儿子,则要么将左边比它小的最大数放到其位置,要么将右边比它大的最小数放到其位置;
element=np->element;
np->element=delete_node(replace); //即最后通过删除一个叶节点(最大值或最小值),将其值放到删除值节点的位置;
return element;
}
}
void insert_node_to_nonempty_tree(link tr,link np) //当树非空的时候,通过比较数的大小进行插入;
{
if(np->element<=tr->element)
{
if(tr->lchild==NULL)
{
tr->lchild=np;
np->parent=tr;
return;
}
else insert_node_to_nonempty_tree(tr->lchild,np);
}
else
{
if(tr->rchild==NULL)
{
tr->rchild=np;
np->parent=tr;
return;
}
else insert_node_to_nonempty_tree(tr->rchild,np);
}
}
link insert_value(link tr,int value) //将value插入到树中,里面需要判断树是否是空的是否需要跳转到插入非空树函数;
{
link np;
np=(link)malloc(sizeof(Node));
np->element=value;
np->parent=np->lchild=np->rchild=NULL;
if(tr==NULL)tr=np;
else
{
insert_node_to_nonempty_tree(tr,np);
}
return tr;
}
int main()
{
link tr;
link np;
int element;
tr=NULL;
tr=insert_value(tr,19);
tr=insert_value(tr,4);
tr=insert_value(tr,2);
tr=insert_value(tr,8);
tr=insert_value(tr,81);
tr=insert_value(tr,101);
printf("FirstTree:\n");
print_sorted_tree(tr);
np=find_value(tr,8);
if(np!=NULL)
{
delete_node(np);
printf("Deletion:\n");
print_sorted_tree(tr);
}
return 0;
}
第六次作业:
1、(一棵树,给一个节点求以其作为根节点的子树的所有value和和value中的最大值,输入时通过给出每个点的父节点存储)这题可能会先认为需要对每个节点存储其儿子节点,那会相对复杂一些,可以通过逆向的存储父节点,然后从后往前计算value和就可以解决;题目博客链接
2、(一棵二叉树,每从一个节点到另一个节点步数就加一,求第一次到指定节点的步数)可以通过深搜的思路,每个节点有到该点的步数step,是否访问vis,当前权值val,左儿子,右儿子,然后根据深搜,每次往下搜步数加一,同步到每个之前未经过的到达的节点,搜到底之后往上返回父节点时步数也加一;题目博客链接


