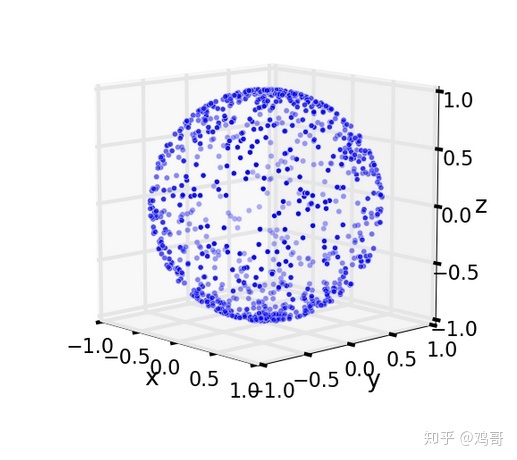
球面均匀采样

写games101作业七的时候，计算间接光照的时候需要对着色点所在的半球面进行一次均匀采样来获得其他物体到着色点的入射光的方向。但是框架中的采样函数我实在看不懂

Vector3f Material::sample(const Vector3f &wi, const Vector3f &N){
	switch(m_type){
		case DIFFUSE:
		{
			// uniform sample on the hemisphere
			float x_1 = get_random_float(), x_2 = get_random_float();
			float z = std::fabs(1.0f - 2.0f * x_1);
			float r = std::sqrt(1.0f - z * z), phi = 2 * M_PI * x_2;
			Vector3f localRay(r*std::cos(phi), r*std::sin(phi), z);
			return toWorld(localRay, N);
			break;
		}
	}
}

为了搞清楚这里采样的原理，搜索了一下相关知识。
本文参考了球谐光照与PRT学习笔记（二）：蒙特卡洛积分与球面上的均匀采样和球面采样 Spherical Sampling以及逆变换采样 (inverse transform sampling) 的原理这三篇博客

对球面的均匀采样

由于我们采样的结果是着色点的入射光方向，因此我们可以通过球坐标系的两个分量：$ (\theta,\phi) $来表示采样结果。

直接对\((\theta,\phi)\)进行均匀采样

直接在\((\theta,\phi)\)进行均匀采样即：

\[\begin{cases} \theta=\xi_x,&\xi_x \sim U(0，1)\\ \phi=\xi_y,&\xi_y \sim U (0,1) \end{cases} \]

但是这样得到的采样结果不是均匀分布

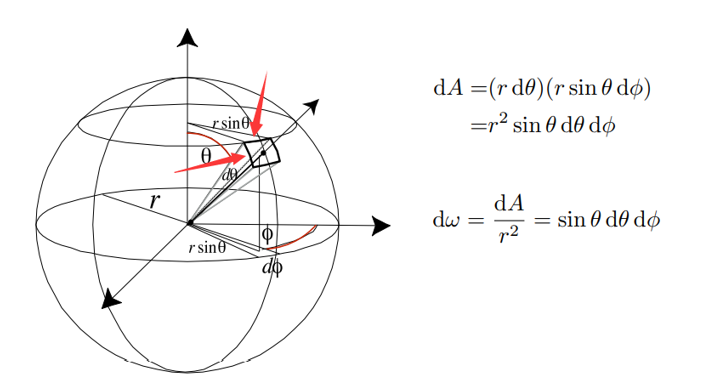
为什么采样结果不均匀呢？原作者提供了一种直观的理解方式：球面可以看作垂直于\(z\)轴的圆的累加，对\(\phi\)采样即是对这些圆的采样，由于这些圆的半径不同，根据圆弧长度与半径和角度之间的关系(如下图所示)圆上采样点之间的距离也不同，因此球面上的采样并不均匀

面积微元 \(dA=r^2sin\theta d\theta d\phi\)，当\(sin\theta\)小的时候立体角也小，面积微元也更小，因此采样点更加密集，随着\(sin\theta\)的增大，立体角也不断增大，面积微元也更大，因此采样点更加稀疏。所以采样结果在球面的两极更加密集。因此直接对\((\theta,\phi)\)均匀采样无法得到对球面均匀采样的结果。

将均匀随机变量映射到\((\theta,\phi)\)进行采样

我们已知由于立体角在不同的\(\theta\)下大小并不相同，这就造成了不同角度下面积微元内的样本密度不同，我们需要构造新的映射方式：

\[\begin{cases} \theta=f(\xi_x),&\xi_x \sim U(0,1)\\ \phi=g(\xi_y),&\xi_y \sim U(0,1) \end{cases} \]

使得在不同角度下的面积微元的样本密度保持一致。
考虑对单位球面采样的情况下，设\(p(v)\)为采样的概率密度函数，\(v\)为采样方向，理想状态下即均匀采样下\(p(v)\)是一个常数，由于单位球面立体角为\(4\pi\)，即\(p(v)=1/4\pi\)。单位球面下面积微元内的采样概率与单位立体角内的采样概率相等，即:

\[P(A)=\int p(v)dw=1/4\pi dw=1/4\pi sin\theta d\theta d\phi \]

用\((\theta,\phi)\)表达的概率密度函数为\(p(\theta,\phi)=dP(A)/d\theta d\phi=1/4\pi sin\theta.\)
现在我们有了理想状态下的概率分布函数\(p(\theta,\phi)\)，还需要求出\((\theta,\phi)\)与\((\xi_x,\xi_y)\)之间的映射关系，我们可以通过Inverse Transform Sampling来得到二者之间的映射关系，即通过均匀分布变量\((\xi_x,\xi_y)\),构造出\((\theta,\phi)\leftarrow(F^{-1}_\theta(\xi_x),F^{-1}_\phi(\xi_y))\),使得\(\theta \sim F_\theta(\theta),\phi \sim F_\phi(\phi).\)因此只要求出\(F^{-1}_\theta(\theta)\)与\(F^{-1}_\phi(\phi)\)即可得到映射关系。我们求出\(\theta\)与\(\phi\)的边缘概率密度：

\[\begin{cases} f(\theta)=\int_{0}^{2\pi} p(\theta,\phi)d\phi=sin\theta/2\\ f(\phi)=\int _{0}^\pi p(\theta,\pi)d\theta=1/2\pi \end{cases} \]

根据边缘概率分布函数我们可以求出边缘分布函数：

\[\begin{cases} F_\theta(\theta)=\int_{0}^\theta f(\hat \theta)d\hat \theta={1-cos\theta\over 2}\\ F_\phi(\phi)=\int _{0}^\phi f(\hat \phi)d\hat \phi=\phi/2 \end{cases} \]

这样就得到了\((\theta,\phi)\)与\((\xi_x,\xi_y)\)之间的映射关系：

\[\begin{cases} \theta=arccos(1-2\xi_x)\\ \phi=2\pi\xi_y \end{cases} \]

将球面换成半球面求得的结果即为框架中的采样函数的映射方式。

Inverse Transform Sampling的证明

给定随机变量\(X \sim P_X(x),Y=f(X)\),当f(X)为递增函数时,随机变量\(Y\)的分布函数\(F_Y(y)\)为：

\[F_Y(y)=Pr(Y\le y)=Pr(X\le f^{-1}(y))=F_X(f^{-1}(y)). \]

随机变量\(Y\)的概率密度函数为：

\[P_Y(y)={dF_Y(y)\over dy}={dF_X(f^{-1}(y))\over dy}=P_X(f^{-1}(y)){df^{-1}(y)\over dy}=P_X(x){dx\over dy}. \]

当\(f(x)\)为递减函数时,随机变量\(Y\)的分布函数为：

\[F_Y(y)=Pr(Y\le y)=Pr(X\ge f^{-1}(y))=1-Pr(X\le f^{-1}(y))=1-F_X(f^{-1}(y)). \]

概率密度函数为：

\[P_Y(y)={dF_Y(y)\over dy}={-dF_X(f^{-1}(y))\over dy}=-P_X(f^{-1}(y)){df^{-1}(y)\over dy}=-P_X(x){dx\over dy}. \]

综上：

\[P_Y(y)=P_X(x)|{dx\over dy}| \]

现在给定随机变量\(X \sim U(0,1),Y \sim F_Y(y),Y=f(X)\),令:

\[f(x)=F^{-1}(x) \]

\(F\)为任意分布函数，则\(Y\)的概率密度函数为：

\[P_Y(y)=P_X(x)|{dx\over dy}|=1*|{dF(y)\over dy}|=P(y) \]

因此

\[F_Y(y)=F(y) \]