Milking Grid POJ - 2185 || 最小覆盖子串
最小覆盖子串:
最小覆盖子串(串尾多一小段时,用前缀覆盖)长度为n-next[n](n-pre[n]),n为串长。
当n%(n-next[n])==0时,有最小循环节(就是最小覆盖子串)。
快照:
我对KMP的一些理解(lyp点拨的):pre[i](或next[i])的实质是串str[1..i]的最长且小于i的“相等前、后缀”分别为str[1..pre[i]](前缀)与str[(i-pre[i]+1)..i](后缀),通俗讲就是:使str[1..i]前k个字母与后k个字母相等的最大k值。
KMP算法详解可见:http://blog.csdn.net/fjsd155/article/details/6864233
另外一个结论:
最小覆盖子串(串尾多一小段时,用前缀覆盖)长度为n-next[n](n-pre[n]),n为串长。
证明分两部分:
1-长为n-next[n]的前缀必为覆盖子串。
当next[n]<n-next[n]时,如图a,长为next[n]的前缀A与长为next[n]的后缀B相等,故长为n-next[n]的前缀C必覆盖后缀B;
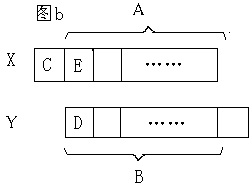
当next[n]>n-next[n]时,如图b,将原串X向后移n-next[n]个单位得到Y串,根据next的定义,知长为next[n]的后缀串A与长为前缀串B相等,X串中的长为n-next[n]的前缀C与Y串中的前缀D相等,而X串中的串E又与Y串中的D相等……可见X串中的长为n-next[n]的前缀C可覆盖全串。
2-长为n-next[n]的前缀是最短的。
如图c,串A是长为n-next[n]的前缀,串B是长为next[n]的后缀,假设存在长度小于n-next[n]的前缀C能覆盖全串,则将原串X截去前面一段C,得到新串Y,则Y必与原串长度大于next[n]的前缀相等,与next数组的定义(使str[1..i]前k个字母与后k个字母相等的最大k值。)矛盾。得证!有人问,为什么Y与原串长大于next[n]的前缀相等?由假设知原串的构成必为CCC……E(E为C的前缀),串Y的构成必为CC……E(比原串少一个C),懂了吧!

首先是这种情况:最长公共前缀后缀不重合
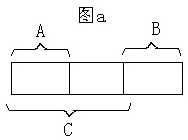
此时显然C串是覆盖子串(C能覆盖C;由于B和A相同而C覆盖A,C也能覆盖B)。为什么是最小的呢?
首先,此时A和B已经是最长的公共前缀后缀,也就是不可能使得公共前缀后缀有重合部分。假设有一个更小的覆盖子串D,那么D右侧的剩余部分E一定长于B,而由于D能覆盖E,E一定是D的开头一部分,E一定是公共前缀后缀,而E大于B,B却是最长的公共前缀后缀,矛盾。
然后是这种情况:最长公共前缀后缀重合
http://www.cnblogs.com/wuyiqi/archive/2012/01/06/2314078.html
http://www.cnblogs.com/chenxiwenruo/p/3546457.html

(端点到底算哪段并不影响)
两段红的为最长公共前缀后缀,表明s[k..j]==s[m..i]。
记s[a..b]为ab.
取x点使得x到j的长度等于j到i的长度,由于xj和ji分别是kj和mi最后的相同长度的一段,xj=ji。
那么kj=kx+xj, mi=mj+ji.
而kj=mi, xj=ji,因此kx=mj。
这一步由kj=mi得到了kx=mj和xj=ji。由kx=mj可以继续按原来的模型证下去,直到最长公共前缀后缀不重叠。可以发现这是一个递归/递推的证明过程。
例1:
ababababa
abababa
abababa
123456789
17=15+67
39=37+89
67=89,17=39-->15=37
15=13+45
37=35+67
15=37,45=67-->13=35
13=1+23
35=3+45
13=35,23=45-->1=3
23=45=67=89,2=4=6=8,1=3=5=7=9,因此也可以视为12=34=56=78

例2:
abababab
ababab
ababab
12345678
16=14+56
38=36+78
16=38,56=78-->14=36
14=12+34
36=34+56
14=36,34=56-->12=34
12=34=56=78

那么为什么是最小的覆盖子串呢?
http://blog.csdn.net/fjsd155/article/details/6866991

如图,根据前一步的证明,原串可以表示为ABABABABA
(A可能为空串,A、B连接起来(表示为AB)就是最小覆盖子串)
假设存在长度小于AB的前缀CD能覆盖全串,那么全串能表示为CDCD...CDC。则将原串X截去前面一段CD,得到新串Y,那么Y能表示为CD...CDC(比全串少一个CD)。显然,Y是原串的公共前后缀,而且Y比原串去掉一个AB得到的公共前后缀要长(因为AB长于CD,相同长度的原串减去CD后的长度一定长于减去AB后的长度),这与原串去掉一个AB得到的公共前后缀是"最长公共前后缀"的条件矛盾。
这道题很容易想错,有一大堆错误题解。
错误方法:
求每行最小覆盖子串的lcm,就是宽度。
hack数据:
2 8 aaabcaaa abababab 4 7 aaaaaaa abababa abcabca abcdabc 2 12 abababababab abcabcabcabc
正解:
http://poj.org/showmessage?message_id=153316
http://blog.csdn.net/maxmercer/article/details/76168361
http://www.cnblogs.com/chenxiwenruo/p/3549967.html
http://blog.sina.com.cn/s/blog_69c3f0410100tyjl.html
代码:
1 #include<iostream> 2 #include<cstring> 3 #include<algorithm> 4 #include<string> 5 using namespace std; 6 int ans_col[80];//ans_col[i]表示0..i-1列可以覆盖整行的行的数量 7 int f[10080],x; 8 int ma_size; 9 int r,c;//m=c 10 string s[10010]; 11 bool cmp(int a,int b) 12 { 13 int i; 14 for(i=0;i<x;i++) 15 if(s[a][i]!=s[b][i]) 16 return true; 17 return false; 18 } 19 void getf(const string& s) 20 { 21 int i=0,j=f[0]=-1; 22 while(i<c) 23 { 24 while(j>=0&&s[i]!=s[j]) j=f[j]; 25 i++;j++; 26 f[i]=j; 27 } 28 } 29 int getf2() 30 { 31 int i=0,j=f[0]=-1; 32 while(i<r) 33 { 34 while(j>=0&&cmp(i,j)) j=f[j]; 35 i++;j++; 36 f[i]=j; 37 } 38 return r-f[r]; 39 } 40 void work(int i) 41 { 42 while(f[i]>=0) 43 { 44 ans_col[c-f[i]]++; 45 i=f[i]; 46 } 47 } 48 int main() 49 { 50 ios::sync_with_stdio(false); 51 int i,t; 52 cin>>r>>c; 53 for(i=0;i<r;i++) 54 { 55 cin>>s[i]; 56 getf(s[i]); 57 work(c); 58 } 59 for(i=1;i<=c;i++) 60 if(ans_col[i]==r) 61 { 62 x=i; 63 break; 64 } 65 //x就是最小的子矩阵列数 66 cout<<getf2()*x; 67 return 0; 68 }
曾经错误:f和row开小,只有80,导致WA。只比较每一行的前宽度个字符,但写成了比较整一行,似乎...并不会导致错误?
1 #include<iostream> 2 #include<cstring> 3 #include<map> 4 #include<algorithm> 5 #include<string> 6 using namespace std; 7 map<string,int> ma;//其实根本就没有用 8 int ans_col[80];//ans_col[i]表示0..i-1列可以覆盖整行的行的数量 9 int f[10080],x; 10 int row[10080],ma_size; 11 int r,c;//m=c 12 string s[10010]; 13 void getf(const string& s) 14 { 15 int i=0,j=f[0]=-1; 16 while(i<c) 17 { 18 while(j>=0&&s[i]!=s[j]) j=f[j]; 19 i++;j++; 20 f[i]=j; 21 } 22 //return m-f[m]; 23 } 24 int getf2() 25 { 26 int i=0,j=f[0]=-1; 27 while(i<r) 28 { 29 while(j>=0&&row[i]!=row[j]) j=f[j]; 30 i++;j++; 31 f[i]=j; 32 } 33 return r-f[r]; 34 } 35 //void work(int i) 36 //{ 37 // if(f[i]>=0) work(f[i]),ans_col[m-f[i]]++; 38 //} 39 void work(int i) 40 { 41 while(f[i]>=0) 42 { 43 ans_col[c-f[i]]++; 44 i=f[i]; 45 } 46 } 47 int main() 48 { 49 ios::sync_with_stdio(false); 50 int i,t; 51 cin>>r>>c; 52 for(i=0;i<r;i++) 53 { 54 cin>>s[i]; 55 getf(s[i]); 56 work(c); 57 } 58 for(i=1;i<=c;i++) 59 if(ans_col[i]==r) 60 { 61 x=i; 62 break; 63 } 64 //x就是最小的子矩阵列数 65 for(i=0;i<r;i++) 66 if(ma.count(s[i])==0) 67 { 68 row[i]=ma_size; 69 ma[s[i]]=ma_size++; 70 } 71 else 72 row[i]=ma[s[i]]; 73 cout<<getf2()*x; 74 return 0; 75 }


