栈 && 教授的测试
卡特兰数：https://blog.csdn.net/wu_tongtong/article/details/78161211
https://www.luogu.org/problemnew/show/P1044
n的答案就是C[n]
证明的话，设n的答案为ans[n]，只要考虑最后一个出栈的数（设为x），那么显然大于x的数在出栈序列中相邻，小于x的数在出栈序列中也相邻，所以这个x产生的贡献为ans[x]*ans[n-x-1]；总答案ans[n]=ans[0]*ans[n-1]+ans[1]*ans[n-2]+...+ans[n-1]*ans[0]=C[n]
http://210.33.19.103/contest/985/problem/5
教授的测试
转眼之间，新学期已经过去几个月了，F大学计算机系的W教授决定对他的学生进行一次测试。为了测试学生对树结构的认识，同时也检验他们的编程能力，教授把测试的内容定为：要求学生们编程按编号顺序打印出节点个数不少于m的所有二叉树。
二叉树编号规则如下：
仅有一个元素的树编号为1。
当满足以下条件之一时，定义二叉树a的编号比b大：
1． a的节点数比b多。
2． 若a的节点数与b相等，且a的左子树编号比b的左子树大。
3． a的节点数和左子树编号都和b相等，且a的右子树编号比b的右子树大。
二叉树的元素用大写X表示。
例如：
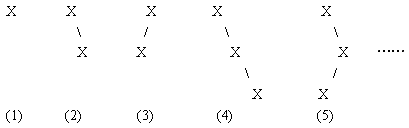
打印二叉树的格式为：
（ 左子树 ）{若左子树为空，则省略} X{根} （ 右子树 ）{若右子树为空，则省略}
例如在上图中，编号为2 的树可表示为：X（X）；
编号为3 的树可表示为：（X）X；
编号为5 的树可表示为：X（（X）X）；
当然当m较大时，检验答案对错的工作也是很繁重的，所以教授只打算对其中的若干个编号的二叉树进行抽查，他想麻烦你在测试开始前把标准答案先准备好（教授的测试卷会事先交给你）。
输入格式：
输入文件为教授的测试卷，至少1行，至多10行，每行一个数N（1<=N<=10^8）,即要抽查的二叉树的编号，以零结束。
输出格式：
输出文件是你求出的标准答案，对每一个编号输出其对应的二叉树，每个二叉树占一行，零不用输出。
样例输入：
2
5
0
样例输出：
X（X）
X（（X）X）
数据范围：
1<=N<=10^8
时间限制：
1000
空间限制：
65536
这回的卡特兰数比较显然，但是实现有一些复杂？
1 #include<cstdio> 2 #include<algorithm> 3 #include<cstring> 4 #include<vector> 5 #include<string> 6 using namespace std; 7 #define fi first 8 #define se second 9 #define mp make_pair 10 #define pb push_back 11 typedef long long ll; 12 typedef unsigned long long ull; 13 typedef pair<int,int> pii; 14 15 ll f[30],g[30]; 16 ll m,n; 17 void dfs(ll n,ll k) 18 { 19 //if(n==0) return ""; 20 ll tt=0,tn=0; 21 while(tt+f[tn]*f[n-tn-1]<=k-1) tt+=f[tn]*f[n-tn-1],tn++; 22 if(tn) putchar('('),dfs(tn,(k-tt-1)/f[n-tn-1]+1),putchar(')'); 23 putchar('X'); 24 if(n-tn-1) putchar('('),dfs(n-tn-1,(k-tt-1)%f[n-tn-1]+1),putchar(')'); 25 } 26 int main() 27 { 28 ll i,j; 29 f[0]=1; 30 for(i=1;i<=20;i++) 31 { 32 for(j=0;j<i;j++) 33 { 34 f[i]+=f[j]*f[i-j-1]; 35 } 36 } 37 g[1]=f[1]; 38 for(i=2;i<=20;i++) g[i]=f[i]+g[i-1]; 39 while(1) 40 { 41 scanf("%lld",&n); 42 if(n==0) break; 43 m=0; 44 while(g[m+1]<=n-1) m++; 45 m++; 46 dfs(m,n-g[m-1]); 47 puts(""); 48 } 49 return 0; 50 }
