图论一（图的存储、遍历、生成树、最短路）

图论基础

图的存储
图的遍历
最小生成树
- kruskal 算法
- prim算法
最短路
- Dijkstra 算法
- Bellman-Ford 算法
- SPFA算法
- Floyd-Warshall 算法

边集数组

采用结构体存储边，包括边的起点、终点、权值等信息，这个结构体数组称为边集数组。

 #define MAXN 100005
int tot;
struct edge{
    int u, v, w;
}es[MAXM];
 
void adde(int u, int v, int w){
    es[++tot].u = u, e[tot].v = v, e[tot].w = w;
}

邻接矩阵

矩阵A可以看做一个二维数组。如果一个有向图中，点$u$到$v$有边相连，权值为$w$, 则$A[u][v] = w$.

如果是无向图，点$u$与$v$的边权为$w$, 则$A[u][v] = A[v][u] = w$

 int arr[MAXN][MAXN];
void adde(int u, int v, int w){ //无向图存储
    arr[u][v] = w;
    arr[v][u] = w;
}

邻接表

将点$u$的所有邻接点插入到以$u$为头的链表中，链表中的元素可以做成结构体，保存边上的信息。每个点都有一个链表。这种存储方式称为邻接表。
下面是使用$STL$中的$list$的示例。

 #define MAXN 100005
struct Edge{
    int v, w;
    Edge(int a = 0, int b = 0){
        v = a, w = b;
    }
};
list<Edge> mylist[MAXN];
void adde(int u, int v, int w){ //无向图存储
    mylist[u].push_back(Edge(v, w));
    mylist[v].push_back(Edge(u, w));
}

邻接表

也可以使用$vector$存储。

 #define MAXN 100005
struct Edge{
    int v, w;
    Edge(int a = 0, int b = 0){
        v = a, w = b;
    }
};
vector<Edge> myvec[MAXN];
void adde(int u, int v, int w){ //无向图存储
    myvec[u].push_back(Edge(v, w));
    myvec[v].push_back(Edge(u, w));
}

邻接表

使用$STL$虽然方便，但是运行速度较慢，如果数据较大，可能超时。较好的方法是使用数组模拟邻接表，它有一个很学术的名字："链式前向星"。

 int head[MAXN];
int tot;
struct Edge{
    int v, w, nxt;
}es[MAXM];
void adde(int u, int v, int w){
    es[++tot].v = v, es[tot].w = w, es[tot].nxt = head[u], head[u] = tot;
    es[++tot].v = u, es[tot].w = w, es[tot].nxt = head[v], head[v] = tot;
}

图的遍历

图的遍历有两种顺序，一种是深度优先搜索，一种是广度优先搜索。
深度优先搜索，就是往优先纵深的方向向搜索，直到无路可走了，则回溯一步，找一条还没有走过的路径，又优先往纵深方向搜索。
如右图，遍历的顺序是：$v1 \to v2 \to v4 \to v8 \to v5 \to v3 \to v6 \to v7$。

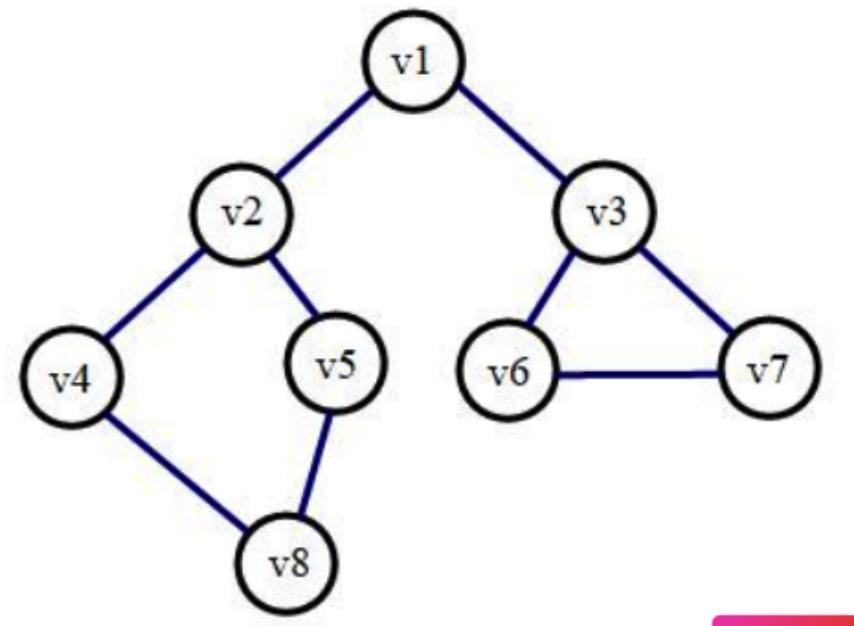
深度优先遍历

深度优先搜索一般采用递归实现。

 //图采用邻接矩阵存储。
int arr[MAXN][MAXN];
void dfs(int r){
    vis[r] = 1;
    cout << r << endl;
    for(int i = 1; i <= n; i++){
        if(arr[r][i] > 0 && !vis[i]){
            vis[i] = 1;
            dfs(i);
        }
    }
}

深度优先遍历

 //图采用邻接表存储。
int head[MAXN];
struct Edge{
    int v, w, nxt;
}es[MAXM];
void dfs(int r){
    vis[r] = 1;
    cout << r << endl;
    for(int i = head[r]; i; i = es[i].nxt){
        int v = es[i].v;
        if(!vis[v]){
            vis[v] = 1;
            dfs(v);
        }
    }
}

广度优先遍历

另一种顺序是广度优先搜索，是优先从周围出发，由近及远，一层层的遍历。
如右图，遍历的顺序是：$v1 \to v2 \to v3 \to v4 \to v5 \to v6 \to v7 \to v8$
.

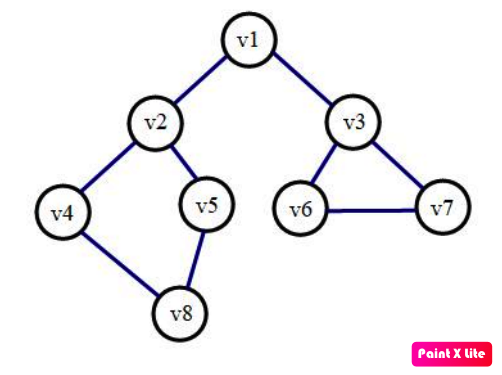
广度优先搜索一般采用队列实现。

 //图用邻接表存储
int head, tail, que[MAXN];
int fir[MAXN];
struct Edge{
    int v, w, nxt;
}es[MAXM];
void bfs(int r){
    que[tail++] = r;
    vis[r] = 1;
    while(head < tail){
        r = que[head++];
        cout << r;
        for(int i = fir[r]; i; i = es[i].nxt){
            if(!vis[es[i].v]){
                que[tail++] = es[i].v;
                vis[es[i].v] = 1;
            }
        }
    }
}

最小生成树

生成树

一个无向图，如果删除一些边，但保留所有的点，最后图变成一棵树，则这棵树称为该图的生成树。

图的生成树不是唯一的。

一个带权的无向图，它的所有生成树中，边权和最小的生成树，称为最小生成树。
最小生成树也不一定是唯一的，但他们的权值和都是最小的。

kruskal算法

这是一个求最小生成树的算法。
假设图中顶点为$n$, 边数为$m$。
我们将所有的边用边集数组存储，并按边权由小到大排序。
一开始，假设每个顶点都是独立的，即图中没有边，现在我们要选择$n-1$条边加上去，将所有的点连通。
我们可以在边集数组中，依次选边，如果当前选的边为$(u,v,w)$, 检查点$u$和$v$之前是否连通，如之前已经连通，则该边不选，继续枚举下一条边；否则，选择该边。
当选择了$n-1$条边后，结束算法，此时即找到了最小生成树。

 struct edge{
    int u, v, w;
    bool operator < (const edge &t)const{
        return w < t.w;   //按边权由小到大排序
    }
}es[MAXM];
void adde(int u, int v, int w){
    es[++ecnt].u = u, es[ecnt].v = v, es[ecnt].w = w;
};
 
for(int i = 1; i <= m; i++){
    if(es[i].u and es[i].v have not connected){ //伪代码: 判断两点是否连通
        select i;   //伪代码，选边
        connect(es[i].u, es[i].v);  // 伪代码: 将两个点连通
        sum += es[i].w;
        cnt++;
    }
    if(cnt == n - 1) break;
}
 
cout << sum << endl;

并查集

如何快速的判断点$u$和$v$是否连通呢？可以使用并查集。
并查集是一种简单但巧妙的数据结构，它可以快速的进行集合的合并、查找等操作。
而完成这一切，只需要一个数组即可。
对一个集合，我们可以任选该集合中的某个元素作为代表。集合可以用一棵树来表示，树根表示该集合的代表。
而这棵树，我们只需要用一个$fa$数组，$fa[i]$表示点$i$的父亲。
一开始，每个节点都各自作为一个集合，每个点都是根节点，此时，对每个点$i$, 都有$fa[i] = 0$.

并查集

查询操作

如果我们想知道某个元素所属的集合，我们只需要找到它所在树的根即可。我们可以沿着父亲一直往上走，直到某个点的父亲为$0$, 则表示到了根节点了。

 int getroot(int r){
    while(fa[r]) r = fa[r]; 
    return r;
}

并查集

合并两个元素所属的集合

对两个元素，先找到各自的根节点，判断根节点是否为同一个，如果是，则不需要合并；否则，将其中一个根节点的$fa$设成另一个根节点即可。

 void my_union(int a, int b){
    int ra = getroot(a);
    int rb = getroot(b);
    if(ra != rb){
        fa[ra] = rb;
    }
}

优化

没有优化的情况下，表示一个集合的树有可能退化成一条链，此时查询操作就变得很慢了。我们需要优化。

第一种优化：按秩合并
即两棵树合并的时候，将深度小的树的根作儿子，深度大的树的根作父亲。这样，合并过后的树，深度增长得较慢。可以证明，它的深度不会超过$logN$.
因为每次合并，只有深度相等的两棵树，其合并过后深度才增加1.可以认为，体量翻一番一倍，深度加1. 那么最终的深度显然不会超过$logN$，因为经过$logN$次后，体量就会达到$n$.
实现时，再多用一个数组$h$，令$h[i]$表示点$i$所在树的深度，合并时判断根节点的$h$值，将深度小的树的根作儿子，深度大的树的根作父亲。如果两棵树的深度相等，合并后，新树的根的$h$值加1；否则，树的深度不变。

并查集

第二种优化:路径压缩
在查询节点$u$所在树的根时，我们需要沿着$u$到根的路径遍历一次。如果路径很长，则遍历耗时较大。那为何不能将这条路径压缩呢？

我们可以把这条路径上的点(除根节点之外）都取下来，接在根的下方，作为根的儿子。反正这棵树，只是表示一个集合而已。树的形态不管怎么样，都能表示集合。扁平化的树明显能更快地找到根节点。
```
 int getroot(int r){
  if(fa[r] == 0) return r;
  return fa[r] = getroot(fa[r]);
}
```

并查集

上面的代码看起来很简单，但因为用了递归，当路径很长时，可能导致爆栈，发生运行时错误。
可以将之修改为非递归代码：

 int stk[MAXN], top;
int getroot(int r){
    while(fa[r]) stk[top++] = r, r = fa[r];
    while(top--){
        fa[stk[top]] = r;
    }
    return r;
}

使用路径压缩的并查集，时间复杂度接近$N\alpha$, 其中$\alpha$可以近似的看做是一个常数。

回到kruskal算法

现在我们可以使用并查集来完善kruskal算法了。

 int kruskal(){
    for(int i = 1; i <= m; i++){
        int ru = getroot(es[i].u), rv = getroot(es[i].v); //采用路径压缩
        if(ru != rv){
            ans += es[i].w;
            ru = fa[rv];
            cnt++;
        }
        if(cnt == n - 1) return ans;
    }
    return -1;
}
int main(){
    sort(es + 1, es + m + 1); //将边集数组按照边权排序 
    kruskal();
}

最小生成树

prim算法

算法描述：一个国王想要开辟疆土。有$n$个城堡，他现在在$1$号城堡，他想要去占领所有的城堡。由于他威望很高，实力很强，他所到之处，莫不臣服。他所付出的代价，只是他的国家到该城堡的距离。于是他每次都选一个离他国土最近的城堡，去征服它。等他征服所有的城堡以后，他所付出的代价，就是$n$个城堡的最小生成树。

最小生成树

prim算法

如何快速找到离国土最近的城堡呢？
如果每次都扫描所有的跨越国境的边，最多需要扫描$m$条，一共要做$n$次，时间复杂度为$O(nm)$。
我们可以对每个还未占领的城堡$i$，记录它到国土内城堡的最小距离,设为$dis[i]$。占领了一个城堡后，设该城堡为$j$，则$dis[i]$可能会变小，需要更新，$dis[i] = min(dis[i], w(i,j))$。
优化过后，时间复杂度为$O(n^2)$.

prim算法

 int prim(int r){
    memset(dis, 0x3f, sizeof dis);
    dis[r] = 0, vis[r] = 1;
    for(int i = 1; i < n; i++){
        for(int j = fir[r]; j; j = es[j].nxt){
            int v = es[j].v;
            if(!vis[v]) dis[v] = min(dis[v], es[j].w);
        }
        res = 0x3f3f3f3f;
        for(int j = 1; j <= n; j++)
            if(vis[j] == 0 && dis[j] < res){
            res = dis[j], r = j;
            }
        if(res == 0x3f3f3f3f) 
        return -1;
        vis[r] = 1;
        ans += res;
    }
    return ans;
}

最短路算法

在一个图中，从某点出发，求它到其他各顶点的最短路径。常见的最短路算法有Dijkstra算法， Bellman-ford算法，SPFA算法， Floyd-warshall算法等。

这些算法各有各的优点和用途。Dijkstra算法用于求单源点最短路，时间复杂度为$O(n^2)$, 采用堆优化后，复杂度可以做到$O(mlogn)$；Bellman-ford算法时间复杂度较高，达到$O(mn)$, 但可以处理负权环; SPFA算法是对Bellman-ford算法的改良版本，速度快了很多，大多数时候能够达到$O(m)$, 但最坏情况下，仍然达到了$O(mn)$; Floyd-warshall算法能够求任意两点之间的最短距离，时间复杂度为$O(n^3)$.

松弛

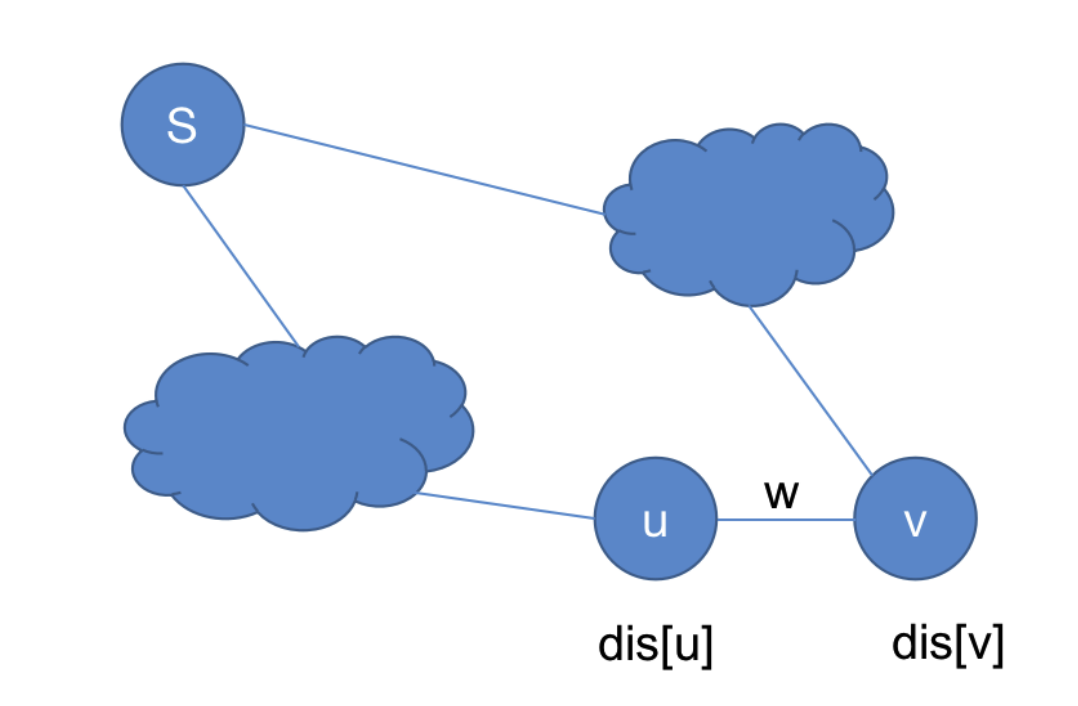
在很多关于图算法的书籍中，都可以看到松弛这个词。简单来讲，松弛就是更新某个顶点的$dis$。比如在求最短路中，设s为源点，u，v为任意两个顶点，u，v有边相连，边的权值为w。设dis[u]中保存了源点s到u的最短估计距离，dis[v]保存了s到v的距离最短估计距离。若现在dis[u]+w<dis[v]，则意味着可以将dis[v]更新为dis[u]+w。

--- ## Dijkstra 算法算法描述如下：设$dis[i]$表示从源点到点$i$的最短距离，初始时，源点的dis值为0，其他点的dis值为无穷大。将点集划分成两个集合，一个集合为$S$,表示已求出$dis$值的点集；另一个集合为$T$，表示还没有求出$dis$值的点集。 1. 一开始，所有点都在$T$中。 2. 在$T$中，找一个$dis$值最小的点，将它加入到$S$中。 3. 对每个新加入$S$中的点，设为$i$, 通过点$i$去更新它的邻接点的$dis$值。比如说，它的一个邻接点为$j$, 则更新$dis[j] = min(dis[j], dis[i] + w(i,j))$. 4. 不断的重复2， 3，直到所有的点都在$S$中，则结束算法。

 void dijkstra(int s){
    memset(dis, 0x3f, sizeof dis);
    dis[s] = 0;
    int cnt = n;
    int res;
    while(--cnt){
        for(int i = fir[s]; i; i = es[i].nxt){
            int v = es[i].v;
            if(!vis[v] && dis[v] >= dis[s] + es[i].w){
                dis[v] = dis[s] + ds[i].w;
            }
        }
        res = 0x3f3f3f3f;
        for(int i = 1; i <= n; i++){
            if(vis[i] == 0 && dis[i] < res){
                res = dis[i], s = i;
            }
        }
        if(res == 0x3f3f3f3f) break;
    }
}

优先队列优化的Dijkstra

普通的Dijkstra算法的时间复杂度为$O(n^2)$。
堆优化的Dijkstra,时间复杂度为$O(MlogN)$。
在普通的Dijkstra中，每次找最小的$dis$都需要遍历一下所有的点。这里可以使用优先队列，优先队列中的元素为结构体，包括点的编号和dis值。每次用$logN$的时间，取出最小的$dis$的点，然后用这个最小的$dis$值，去更新它的邻接点。而更新过后的邻接点，再存入堆中。
这样一来，有的点经过多次更新，可能该点会有多个版本在堆中，取出时打一下标记。只要是取出过的点，再一次取到时，就直接扔了。
时间复杂度为$O(MlogN)$.

 memset(dis, 0x3f, sizeof dis);
    dis[st] = 0;
    myq.push(node(st, 0));
    while(!myq.empty()){
        node tmp = myq.top();
        myq.pop();
        int id = tmp.id, d = tmp.dis;
        if(vis[tmp.id] == 1) continue;
        vis[tmp.id] = 1;
        for(int i = fir[id]; i; i = es[i].nxt){
                if(dis[es[i].v] > dis[id] + es[i].w){
                    dis[es[i].v] = dis[id] + es[i].w;
                    last[es[i].v] = id;
                    myq.push(node(es[i].v, dis[es[i].v]));
                }
           }
    }

SPFA算法
SPFA算法是由西南交通大学段丁凡1994提出的。它采用了队列和松弛技术。先将源点加入队列。然后从队列中取出一个点(此时该点为源点)，对该点的邻接点进行松弛，如果该邻接点松弛成功且不在队列中，则把该点加入队列。如此循环往复，直到队列为空，则求出了最短路径。
判断有无负环：如果某个点进入队列的次数超过N次则存在负环 ( 存在负环则无最短路径,如果有负环则会无限松弛,而一个带n个点的图至多松弛n-1次)

SPFA算法

 struct node{
    int v, w, nxt;
}es[MAXM];
 
bool spfa(int s){
    int l = 1 ,r = 1, temp=0;
    dis[s] = 0;    
    queue[r++] = s;
    inq[s] = 1;
    while(l < r){
        temp = queue[l++];
        inq[temp] = 0;
        for(int i = fir[temp]; i; i = es[i].nxt){
             if(es[i].w + dis[temp] < dis[es[i].v]){
                 path[es[i].v] = temp;
                 dis[es[i].v] = es[i].w + dis[temp];
                 if(inq[es[i].v] == 0){
                     queue[r++] = es[i].v;
                     inq[es[i].v] = 1;
                     if(r > 3 * V + 1)return 0; //一般情况下，节点平均进队3次以上，则可以退出了.
                 }                   
             }
        }     
    }
    return 1;
}

Floyd 算法

Floyd算法是求图中任意两点之间的最短距离。
使用三层循环，第一层循环枚举所有的中间点，第二层循环枚举起点，第三层枚举终点，将起点到终点的距离用经过中间点的路径去更新。

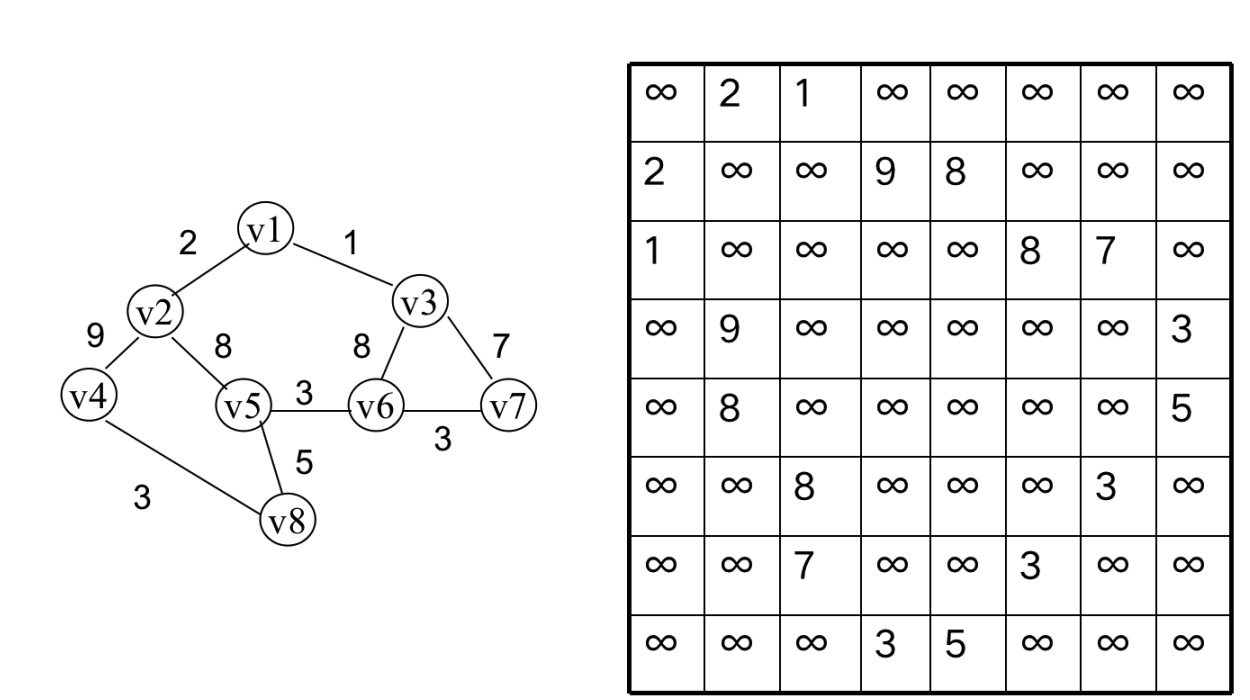
Floyd 算法

 for(int k=0;k<n;k++){//k为中间节点
    for(int i=0;i<n;i++){//i为起点
        for(int j=0;j<n;j++){ //j为终点
            if(i!=k&&i!=j&&k!=j)
                if(arr[i][k]+arr[k][j]<arr[i][j])
                arr[i][j]=arr[i][k]+arr[k][j];
        }
    }
}

拓扑排序

如果将图中的边看做有意义的关系，比如先后关系，大小关系，生成关系，则可以按照这些关系将图中的顶点排序，形成一个线性序列。这种排序方法称为拓扑排序，形成的序列称为拓扑序列。

拓扑排序

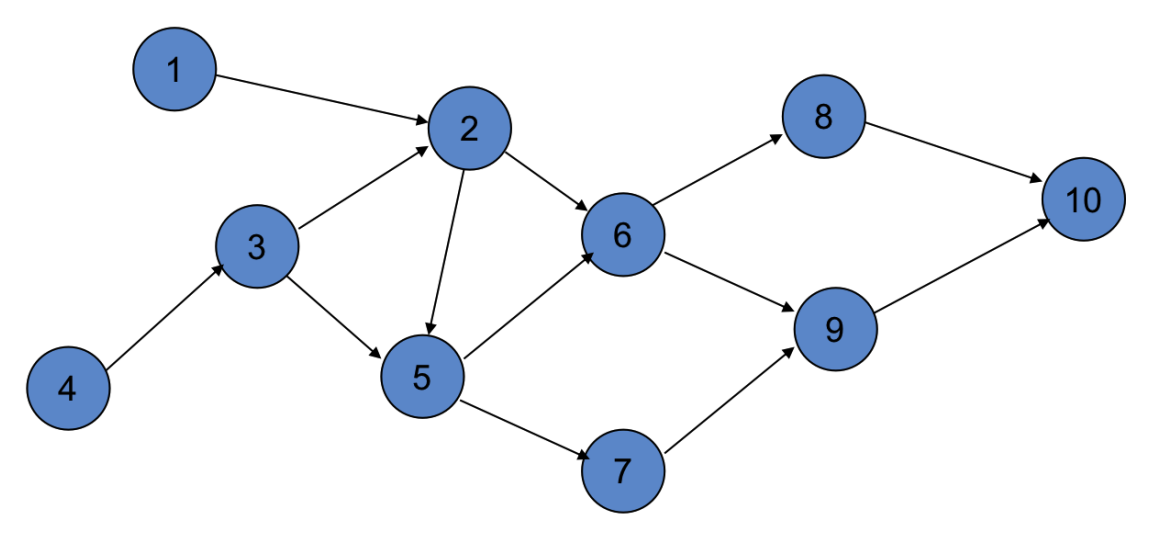
图中的节点代表大学某专业的十门专业课程，边代表它们的先后顺序。现在要在一学年中学完这十门课，请安排一个合理的顺序。可以看出：
$1 \to 4 \to 3 \to 2 \to 5 \to 6 \to 7 \to 8 \to 9 \to 10$是一个合理的顺序。
$4 \to 3 \to 1 \to 2 \to 5 \to 6 \to 8 \to 7 \to 9 \to 10$ 是另一个合理的顺序。
这两个序列都是该图的拓扑序列。

拓扑排序

 for(int i = 1; i <= n; i++){
    if(deg[i] == 0) myq.push(i);
}
while(!myq.empty()){
    int tmp = myq.top();
    myq.pop();
    ans[id++] = tmp;
    for(int i = fir[tmp]; i; i = es[i].nxt){
        deg[es[i].v]--;
        if(deg[es[i].v] == 0)myq.push(es[i].v);
    }
 }
 if(id < n)printf("no solution\n");
 else{
    for(int i = 0; i < n; i++)printf("%d ", ans[i]);
    printf("\n");
}

posted @ 2024-11-01 23:11 hefenghhhh 阅读(89) 评论(0) 编辑收藏举报

刷新页面返回顶部

登录后才能查看或发表评论，立即登录或者逛逛博客园首页

相关博文：

· 差分约束系统

· 一笔画问题

· 图论2021版

· 图论总结——最短路

阅读排行：
· TypeScript + Deepseek 打造卜卦网站：技术与玄学的结合
· 阿里巴巴 QwQ-32B真的超越了 DeepSeek R-1吗？
· 【译】Visual Studio 中新的强大生产力特性
· 2025年我用 Compose 写了一个 Todo App
· 张高兴的大模型开发实战：（一）使用 Selenium 进行网页爬虫

公告

昵称： hefenghhhh
园龄： 17年1个月
粉丝： 12
关注： 4

+加关注

2025年3月

日

一

二

三

四

五

六

	#define MAXN 100005
	int tot;
	struct edge{
	int u, v, w;
	}es[MAXM];

	void adde(int u, int v, int w){
	es[++tot].u = u, e[tot].v = v, e[tot].w = w;
	}

	int arr[MAXN][MAXN];
	void adde(int u, int v, int w){ //无向图存储
	arr[u][v] = w;
	arr[v][u] = w;
	}

	#define MAXN 100005
	struct Edge{
	int v, w;
	Edge(int a = 0, int b = 0){
	v = a, w = b;
	}
	};
	list<Edge> mylist[MAXN];
	void adde(int u, int v, int w){ //无向图存储
	mylist[u].push_back(Edge(v, w));
	mylist[v].push_back(Edge(u, w));
	}

	int head[MAXN];
	int tot;
	struct Edge{
	int v, w, nxt;
	}es[MAXM];
	void adde(int u, int v, int w){
	es[++tot].v = v, es[tot].w = w, es[tot].nxt = head[u], head[u] = tot;
	es[++tot].v = u, es[tot].w = w, es[tot].nxt = head[v], head[v] = tot;
	}

	//图采用邻接矩阵存储。
	int arr[MAXN][MAXN];
	void dfs(int r){
	vis[r] = 1;
	cout << r << endl;
	for(int i = 1; i <= n; i++){
	if(arr[r][i] > 0 && !vis[i]){
	vis[i] = 1;
	dfs(i);
	}
	}
	}

	//图采用邻接表存储。
	int head[MAXN];
	struct Edge{
	int v, w, nxt;
	}es[MAXM];
	void dfs(int r){
	vis[r] = 1;
	cout << r << endl;
	for(int i = head[r]; i; i = es[i].nxt){
	int v = es[i].v;
	if(!vis[v]){
	vis[v] = 1;
	dfs(v);
	}
	}
	}

	//图用邻接表存储
	int head, tail, que[MAXN];
	int fir[MAXN];
	struct Edge{
	int v, w, nxt;
	}es[MAXM];
	void bfs(int r){
	que[tail++] = r;
	vis[r] = 1;
	while(head < tail){
	r = que[head++];
	cout << r;
	for(int i = fir[r]; i; i = es[i].nxt){
	if(!vis[es[i].v]){
	que[tail++] = es[i].v;
	vis[es[i].v] = 1;
	}
	}
	}
	}

	struct edge{
	int u, v, w;
	bool operator < (const edge &t)const{
	return w < t.w; //按边权由小到大排序
	}
	}es[MAXM];
	void adde(int u, int v, int w){
	es[++ecnt].u = u, es[ecnt].v = v, es[ecnt].w = w;
	};

	for(int i = 1; i <= m; i++){
	if(es[i].u and es[i].v have not connected){ //伪代码: 判断两点是否连通
	select i; //伪代码，选边
	connect(es[i].u, es[i].v); // 伪代码: 将两个点连通
	sum += es[i].w;
	cnt++;
	}
	if(cnt == n - 1) break;
	}

	cout << sum << endl;

	void my_union(int a, int b){
	int ra = getroot(a);
	int rb = getroot(b);
	if(ra != rb){
	fa[ra] = rb;
	}
	}

	int getroot(int r){
	if(fa[r] == 0) return r;
	return fa[r] = getroot(fa[r]);
	}

	int stk[MAXN], top;
	int getroot(int r){
	while(fa[r]) stk[top++] = r, r = fa[r];
	while(top--){
	fa[stk[top]] = r;
	}
	return r;
	}

	int kruskal(){
	for(int i = 1; i <= m; i++){
	int ru = getroot(es[i].u), rv = getroot(es[i].v); //采用路径压缩
	if(ru != rv){
	ans += es[i].w;
	ru = fa[rv];
	cnt++;
	}
	if(cnt == n - 1) return ans;
	}
	return -1;
	}
	int main(){
	sort(es + 1, es + m + 1); //将边集数组按照边权排序
	kruskal();
	}

	int prim(int r){
	memset(dis, 0x3f, sizeof dis);
	dis[r] = 0, vis[r] = 1;
	for(int i = 1; i < n; i++){
	for(int j = fir[r]; j; j = es[j].nxt){
	int v = es[j].v;
	if(!vis[v]) dis[v] = min(dis[v], es[j].w);
	}
	res = 0x3f3f3f3f;
	for(int j = 1; j <= n; j++)
	if(vis[j] == 0 && dis[j] < res){
	res = dis[j], r = j;
	}
	if(res == 0x3f3f3f3f)
	return -1;
	vis[r] = 1;
	ans += res;
	}
	return ans;
	}

	void dijkstra(int s){
	memset(dis, 0x3f, sizeof dis);
	dis[s] = 0;
	int cnt = n;
	int res;
	while(--cnt){
	for(int i = fir[s]; i; i = es[i].nxt){
	int v = es[i].v;
	if(!vis[v] && dis[v] >= dis[s] + es[i].w){
	dis[v] = dis[s] + ds[i].w;
	}
	}
	res = 0x3f3f3f3f;
	for(int i = 1; i <= n; i++){
	if(vis[i] == 0 && dis[i] < res){
	res = dis[i], s = i;
	}
	}
	if(res == 0x3f3f3f3f) break;
	}
	}

	memset(dis, 0x3f, sizeof dis);
	dis[st] = 0;
	myq.push(node(st, 0));
	while(!myq.empty()){
	node tmp = myq.top();
	myq.pop();
	int id = tmp.id, d = tmp.dis;
	if(vis[tmp.id] == 1) continue;
	vis[tmp.id] = 1;
	for(int i = fir[id]; i; i = es[i].nxt){
	if(dis[es[i].v] > dis[id] + es[i].w){
	dis[es[i].v] = dis[id] + es[i].w;
	last[es[i].v] = id;
	myq.push(node(es[i].v, dis[es[i].v]));
	}
	}
	}

	struct node{
	int v, w, nxt;
	}es[MAXM];

	bool spfa(int s){
	int l = 1 ,r = 1, temp=0;
	dis[s] = 0;
	queue[r++] = s;
	inq[s] = 1;
	while(l < r){
	temp = queue[l++];
	inq[temp] = 0;
	for(int i = fir[temp]; i; i = es[i].nxt){
	if(es[i].w + dis[temp] < dis[es[i].v]){
	path[es[i].v] = temp;
	dis[es[i].v] = es[i].w + dis[temp];
	if(inq[es[i].v] == 0){
	queue[r++] = es[i].v;
	inq[es[i].v] = 1;
	if(r > 3 * V + 1)return 0; //一般情况下，节点平均进队3次以上，则可以退出了.
	}
	}
	}
	}
	return 1;
	}

	for(int k=0;k<n;k++){//k为中间节点
	for(int i=0;i<n;i++){//i为起点
	for(int j=0;j<n;j++){ //j为终点
	if(i!=k&&i!=j&&k!=j)
	if(arr[i][k]+arr[k][j]<arr[i][j])
	arr[i][j]=arr[i][k]+arr[k][j];
	}
	}
	}

	for(int i = 1; i <= n; i++){
	if(deg[i] == 0) myq.push(i);
	}
	while(!myq.empty()){
	int tmp = myq.top();
	myq.pop();
	ans[id++] = tmp;
	for(int i = fir[tmp]; i; i = es[i].nxt){
	deg[es[i].v]--;
	if(deg[es[i].v] == 0)myq.push(es[i].v);
	}
	}
	if(id < n)printf("no solution\n");
	else{
	for(int i = 0; i < n; i++)printf("%d ", ans[i]);
	printf("\n");
	}

程序改变世界，教育创造未来

图论一（图的存储、遍历、生成树、最短路）

图论基础

边集数组

邻接矩阵

邻接表

邻接表

邻接表

图的遍历

深度优先遍历

深度优先遍历

广度优先遍历

最小生成树

生成树

kruskal算法

并查集

并查集

查询操作

并查集

合并两个元素所属的集合

优化

并查集

并查集

回到kruskal算法

最小生成树

prim算法

最小生成树

prim算法

prim算法

最短路算法

松弛

优先队列优化的Dijkstra

SPFA算法

Floyd 算法

Floyd 算法

拓扑排序

拓扑排序

拓扑排序

公告

搜索

常用链接

我的标签

随笔分类

随笔档案

阅读排行榜