python实现自动生成小学四则运算题目（软工第二次项目作业）

前言

软件工程	传送带
作业要求	传送带
作业目标	结对编程：代码实现、性能分析、异常处理说明、记录PSP表格
代码见:
github
个人信息:朱育清 3118005437 信安二班
我的partner
个人信息：林泓 3118005370 信安一班

PSP

PSP2.2	Personal Software Process Stages	预估耗时（分钟）	实际耗时（分钟）
Planning	计划	100	100
· Estimate	· 估计这个任务需要多少时间	600	500
Development	开发	200	300
· Analysis	· 需求分析 (包括学习新技术)	150	200
· Design Spec	· 生成设计文档	30	50
· Design Review	· 设计复审	30	40
· Coding Standard	· 代码规范 (为目前的开发制定合适的规范)	30	50
· Design	· 具体设计	100	120
· Coding	· 具体编码	200	300
· Code Review	· 代码复审	30	50
· Test	· 测试（自我测试，修改代码，提交修改）	60	30
Reporting	报告	30	50
· Test Repor	· 测试报告	30	50
· Size Measurement	· 计算工作量	10	10
· Postmortem & Process Improvement Plan	· 事后总结, 并提出过程改进计划	30	30
	合计	400	500

具体实现

利用二叉树来生成运算式

注：以下图中，长方形表示运算符节点，三角形表示尚未确定的节点，圆圈表示为运算数的节点
以生成三个操作符为例

First step

先生成一个根节点添加到一个列表里，并作为运算符节点

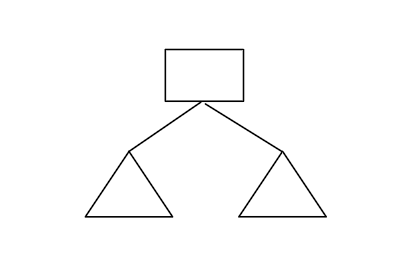
Second step

将已选来当作运算符节点的节点移除出列表，然后将两个新增的子节点添加列表里，从列表两个节点中随机选一个当运算符节点

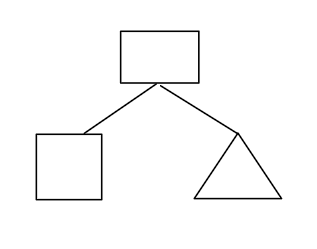
Third step

移除已选的节点，将新增的子节点添加列表，从列表的三个节点中随机选一个当运算符节点

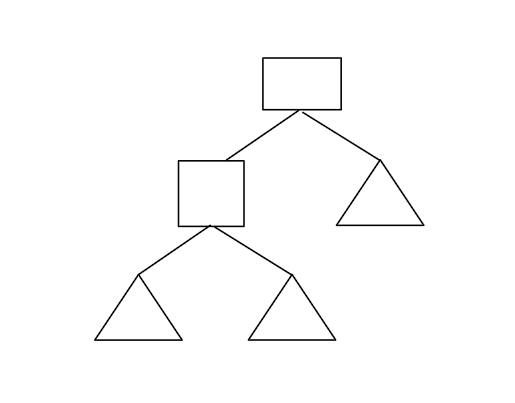
Fourth step

移除已选的节点，将新增的子节点添加到列表，从列表的四个节点中随机选一个充当运算符节点

Fifth step

此时已经生成三个符号节点，只需要将树中的剩余节点赋值为操作数即可

具体代码实现如下：
主要的tree类和node类：

class Node:
    # 节点类
    def __init__(self):
        self.type = 0  # 节点的类别：{初始化：0， 数字：1， 操作符：2， }
        self.operator = None  # 操作符类型
        self.number = None  # 操作结果
        self.left = None  # 左子树
        self.right = None  # 右子树
        self.op_priority = {'+': 1, '-': 1, '*': 2, '/': 2}  # 设置操作符的优先级
     class Tree:
class Tree:
    # 树类
    def __init__(self):
        self.root = Node()
        self.op_list = ["+", "-", "*", "/"]                               # 根节点的符号类型
        self.type = [1, 2]                                           # 节点类型，1表示整数，2表示分数
        self.middle_formula = list()                                      # 中缀表达式
        self.after_formula = list()                                       # 后缀表达式
        self.formula = list()                                             # 格式化后的表达式
        self.answer = list()                                              # 格式标准化的答案

二叉树的生成:（tree类的方法）

    def create(self, num_range, number):
        num = 0
        while num < number:    # number表示生成表达式的数量
            degree = random.choice([1, 2, 3])  # 随机选择操作符的数量，最多有三个
            empty_node = [self.root]
            for _ in range(degree):
                node = random.choice(empty_node)
                empty_node.remove(node)
                node.operator = random.choice(self.op_list)
                node.type = 2
                node.left = Node()
                node.right = Node()
                empty_node.append(node.left)
                empty_node.append(node.right)

            for node in empty_node:
                node.type = 1
                num_type = random.choice(self.type)   # 随机选择，生成整数还是小数
                if num_type == 1:
                    node.number = random.randint(1, number)
                else:
                    node.number = Fraction(random.randint(1, num_range), random.randint(1, num_range))

关于小括号的添加

添加小括号是为了处理优先级问题，所以当我们的父母节点的运算符优先级大于或者等于我们的子节点的子树时，便在我们的子树添加小括号
具体代码实现如下:

  def get_formula(self):   # 获取我们的中序表达式，在这里根据添加小括号以区别优先级
        formula = list()
        if self.type == 1:
            return [self.number]
        elif self.type == 2:
            if self.left.type == 2 and \
                self.op_priority[str(self.operator)] > self.op_priority[str(self.left.operator)]:
                '''处理左子树'''
                formula.append('(')                                      # 当我们的父母节点的操作符的优先级大于或等于我们的孩子节点的时候，在子树添加小括号
                formula += self.left.get_formula()
                formula.append(')')
            else:
                formula += self.left.get_formula()

            formula.append(self.operator)                                 # 中间节点的处理

            '''当右孩子是操作符时'''
            if self.right.type == 2 and \
                    self.op_priority[str(self.operator)] >= self.op_priority[str(self.right.operator)]:
                formula.append('(')                                        # 当我们的父母节点的操作符优先级大于或等于我们的孩子节点时，在子树添加小括号
                formula += self.right.get_formula()
                formula.append(')')
            else:
                formula += self.right.get_formula()
            return formula

关于运算结果的计算

利用后缀表达式来计算

这里引入一种数据结构:后缀表达式，也叫逆波兰表达式
这里先说明一下中缀表达式:中缀表达式是一种通用的算术或逻辑公式表示方法，操作符以中缀形式处于操作数的中间。中缀表达式是人们常用的算术表示方法。
譬如(3 + 4) × 5 - 6，就是用中缀表达式去记录的
但是虽然人的大脑很容易理解与分析中缀表达式，人是有思维能力的，能根据操作符的位置，以及操作符的优先级别能算出该表达式的结果。但对计算机来说中缀表达式却是很复杂的。计算机必须要向前（从左到右）来读取操作数和操作符，等到读取足够的信息来执行一个运算时，找到两个操作数和一个操作符进行运算，有时候如果后面是更高级别的操作符或者括号时，就必须推迟运算，必须要解析到后面级别高的运算，然后回头来执行前面的运算。我们发现这个过程是极其繁琐的，而计算机是一个机器，只认识高低电平，想要完成一个简单表达式的计算，我们可能要设计出很复杂的逻辑电路来控制计算过程。可见这个中缀表达式对于计算机不够友善。
所以我们来看看计算机可以如何计算后缀表达式。
例如现在有后缀表达式 6 5 2 3 + 8 * + 3 + *
计算如下：
前四个操作数放入栈中，此时栈变为：

下面读到一个'+'号，所以3和2从栈中弹出并他们的和5被压入栈中

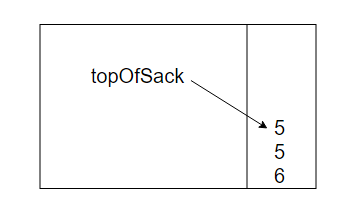
接着，8进栈

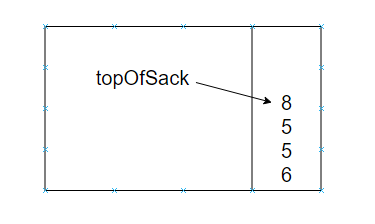
现在见到一个*号，因此8和5弹出并且5*8=40进栈

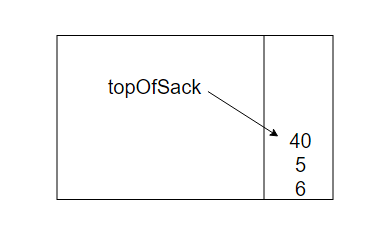
接着又见到一个'+'号，因此40和5被弹出并且5+40=45进栈

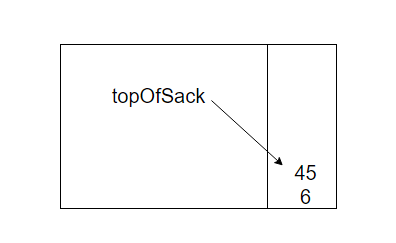
现在将3压入栈中

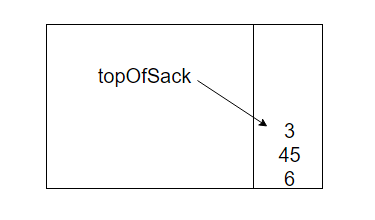
然后'+'使得3和45从栈中弹出并将45+3=48压入栈中

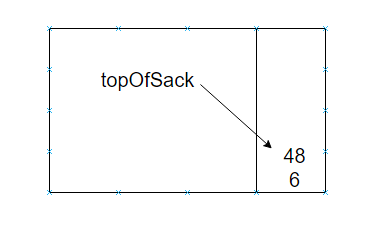
最后，遇到一个*号，从栈中弹出48和6；将6*48压入栈中

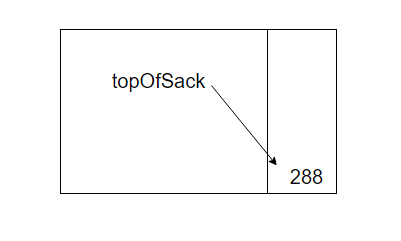
所以我们可以利用后缀表达式来计算最终结果，具体代码如下:

class Calculation:
    def eval(op, a, b):                     # 当只有一个操作符的计算
        answer = 0
        if op == "+":
            answer = operator.add(a, b)
        elif op == "-":
            if operator.lt(a, b):           # a是否小于b
                raise NegativeError()       # 当被减数大于减数的时候，抛出异常
            else:
                answer = operator.sub(a, b)
        elif op == "*":
            answer = operator.mul(a, b)
        elif op == "/":
            answer = operator.truediv(a, b)
            if isinstance(answer, float):    # 当答案为浮点数，转换为分数
                answer = operator.truediv(Fraction(a), Fraction(b))
        return answer

    def get_answer(formula_list):            # 后缀表达式的计算
        num_list = list()
        for formula in formula_list:
            if isinstance(formula, int) or isinstance(formula, Fraction):
                num_list.append(formula)
            else:
                b = num_list.pop()
                a = num_list.pop()
                res = Calculation.eval(formula, a, b)
                num_list.append(res)
        return num_list.pop()
'''

中缀表达式转后缀表达式

因为最终算式的计算结果是用后缀表达式来计算的，所以需要将中缀表达式转化为后缀表达式
当读到一个操作数时，立即把它放到输出中。操作符不立即输出，从而必须先存在栈中。当遇到左括号时，我们也放入栈中。如果遇到一个右括号，则将栈元素弹出，将弹出的符号写出直至遇到一个左括号。如果我们遇到任何其他符号，那么我们从栈中弹出元素直至发现优先级更低的元素为止。
譬如

a+b*c+(d*e+f)*g

首先符号a被读入，于是它被传向输出。然后,'+'被读入并被放到栈中。接下来b读入并流向输出。此时状态:

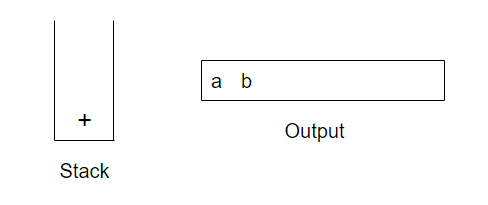
接着*被读入。操作符的栈顶元素比*的优先级低，故没有输出且*进栈。接着，c被读入并输出。至此，我们有

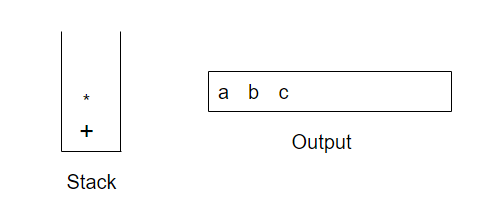
后面的符号是一个+号。检查一下我们发现，需要将*从栈弹出并把它放到输出中；弹出栈中的+号，该算符不比刚刚遇到的+号优先级低而是由相同的优先级；然后，将刚刚遇到的+号压入栈中

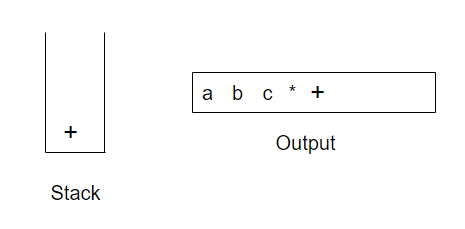
下一个被读到的符号是一个（，由于有高的优先级，因此把它放到栈中。然后d,读入并继续进行

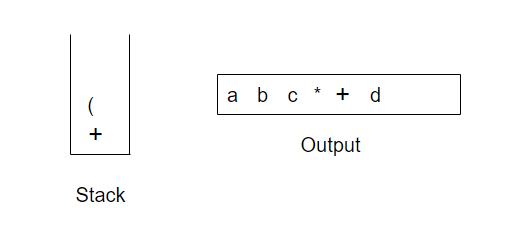
我们又读到一个*。由于除非正在处理闭括号否则开括号不会从栈中弹出，因此没有输出。下一个是e，它被读入并输出

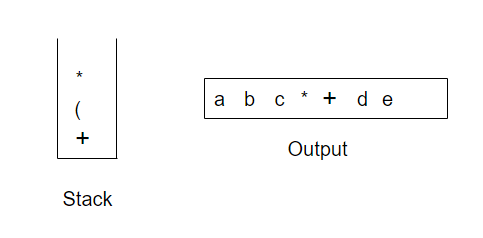
再往后读到的符号是+。我们将*弹出并输出，然后将+压入栈中。这之后，我们读到f并输出

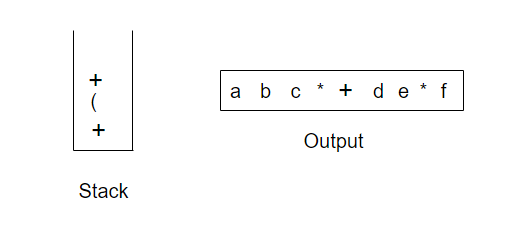
现在我们读到一个),因此将栈元素直到（弹出，我们将一个+号输出

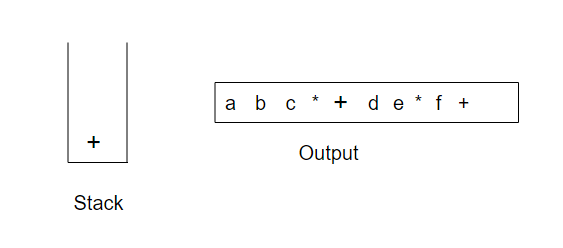
下面又读到一个*;该算符被压入栈中。然后g被读入并输出

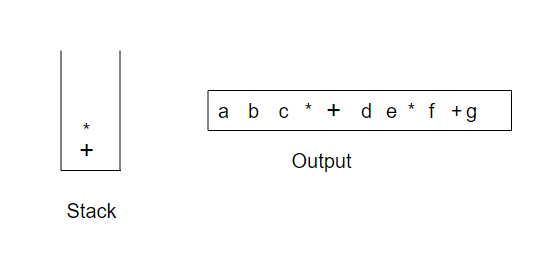
现在输入为空，因此我们将栈中的符号全部弹出并输出，直到栈变为空栈

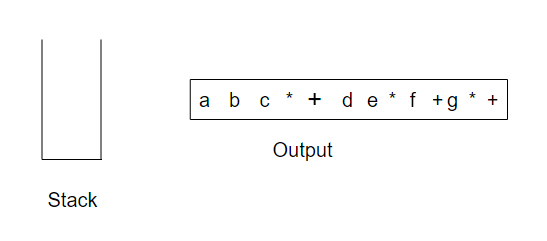
具体代码实现:

    def get_after_formula(formula):     # 将中缀表达式转换为后缀表达式
        op_priority = {'(': 0, ')': 0, '+': 1, '-': 1, '*': 2, '/': 2}
        postfix_formula = list()  # 输出
        op_list = list()      # 充当栈
        for item in formula:
            if isinstance(item, int) or isinstance(item, Fraction):
                # 如果为数字直接输出
                postfix_formula.append(item)
            elif item == '(':
                # 输入时把左括号看坐最低优先级的，直接入栈
                op_list.append(item)
            elif item == ')':
                # 如果为右括号,优先级别最高，将里面的所有操作符输出
                while op_list[-1] != '(':
                    postfix_formula.append(op_list.pop())
                op_list.pop()  #
            else:
                # 如果为操作符,比较该操作符和栈顶的操作符优先级作比较
                # 如果优先级大于栈顶元素压栈,否则将op_list中优先级大于或等于该操作符的元素输出
                # 最后压栈
                while len(op_list) > 0 and op_priority[op_list[-1]] >= op_priority[item]:
                    postfix_formula.append(op_list.pop())
                op_list.append(item)

        while op_list:
            # 将剩余的op_list出栈
            postfix_formula.append(op_list.pop())

        return postfix_formula

关于代码优化

这里考虑的优化主要在于查重这个步骤.因为我们的中序表达式是通过一个列表来装载的,而我们的运算符最多有三个,二叉树的形状总共就几样,可以利用穷举法结合python中列表的切片等操作来验证,但是后来转念一想,这样的话,代码的效率大大降低,所以最终敲定用一个比较"流氓的"查重方法,将每一个生成式的答案与我们已经生成的题库中的答案比对,只要答案一致便剔除

if answer in self.answer:          # 重复度查询，只要计算答案一致，都不加入我们的题库，从结果解决问题
      continue

异常处理

主要考虑到两点，一个是我们的真分数的分母不可为0，一个是我们的我们的表达式结果不可为负数。
对于第一个，用了python本身的内置异常 ZeroDivisionError
对于第二个，我们本身定义了一个异常类：

#  自定义一个表达式为表达式为负数的类
class NegativeError(Exception):
    def __init__(self):
        super(NegativeError, self).__init__()

性能分析

代码覆盖率

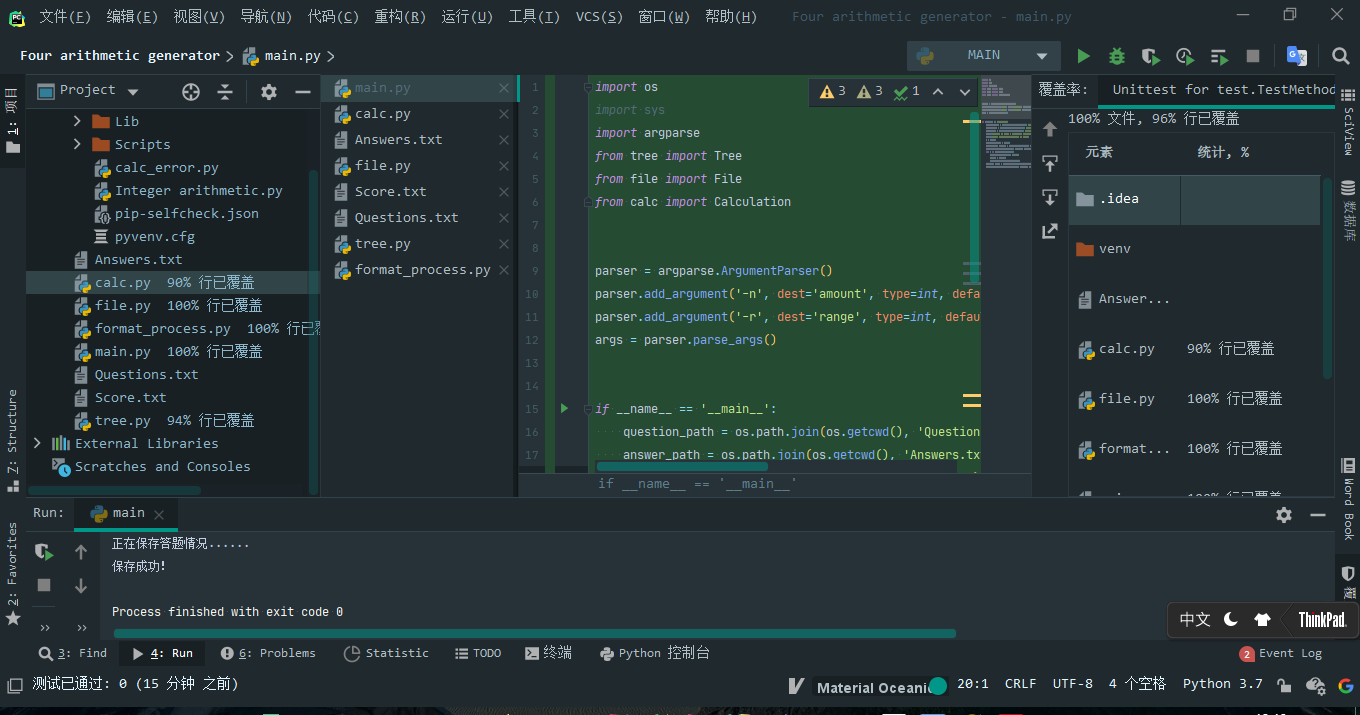
可以看到，代码覆盖率为96%，是因为有些异常处理没有被触发.

运行时间

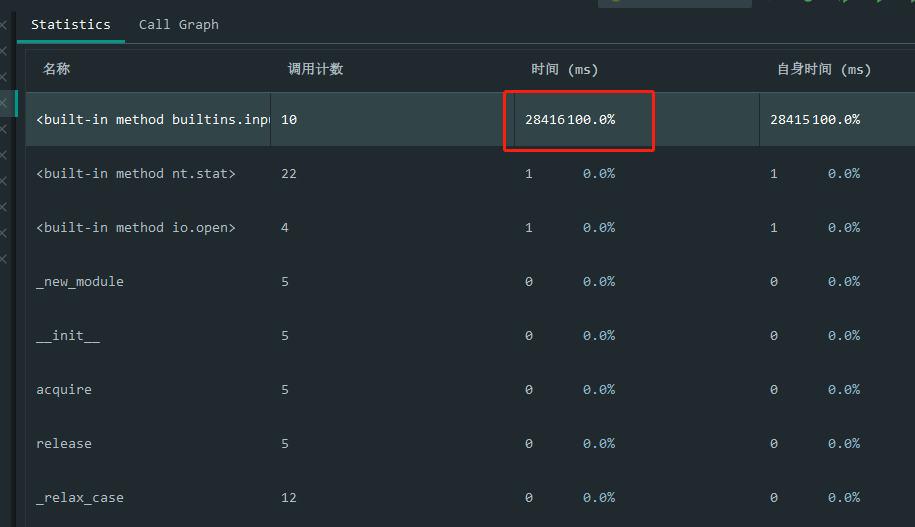
可以看到，由于我们答题时间太长,导致我们的程序中的其他代码运行时间占比无限趋近于0

正确率测试

我们自己手工计算了10道题，对比它算的答案，发现正确率为百分之一百

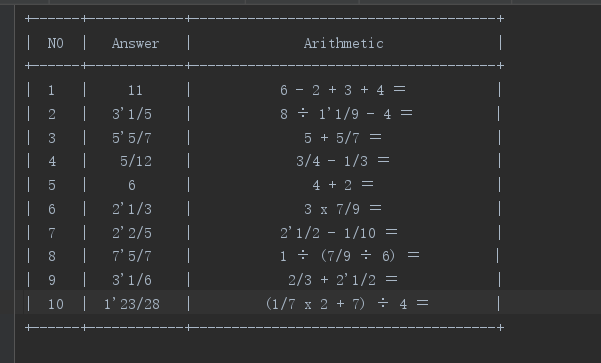
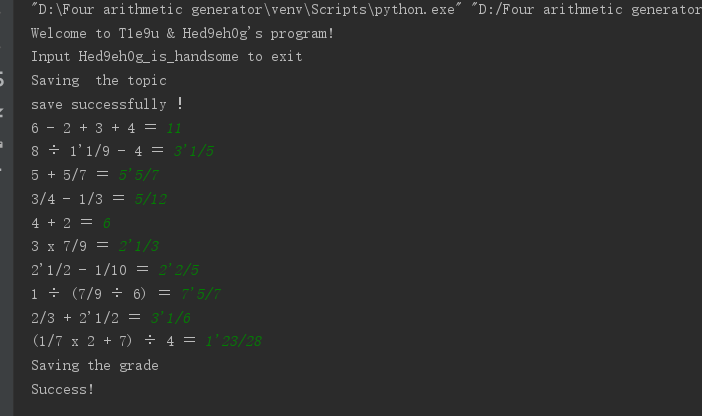
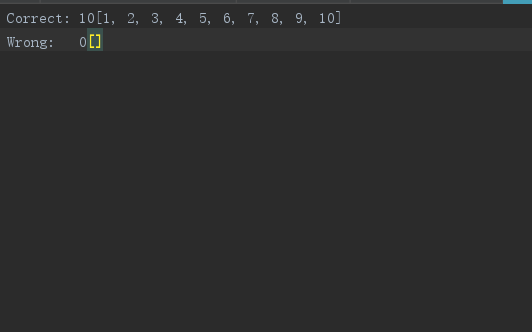
参考

以上后缀表达式的计算方法以及转换参考于<<数据结构与算法分析>>