大学微积分 AB 第六单元-3:变革的整合与积累(微积分基本定理与定积分、不定积分和不定导数、寻找不定积分和积分、𝘶 替代介绍不定积分和定积分、使用长除法进行积分、利用完成平方和 arctan(x) 的导数进行积分)


微积分基本定理与定积分
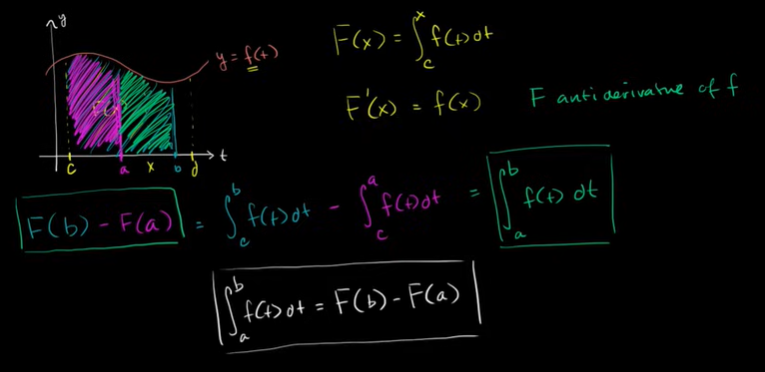
例子:

不定积分和不定导数


例子:

例子2:

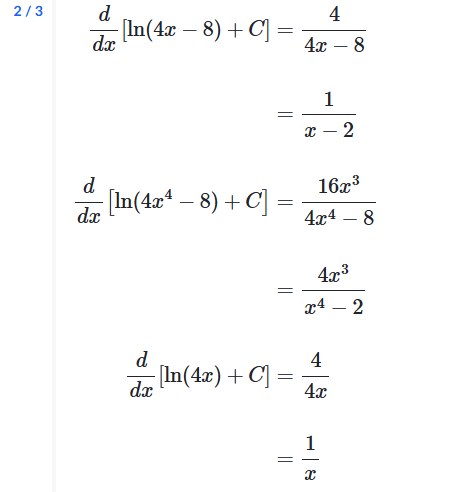

例子:
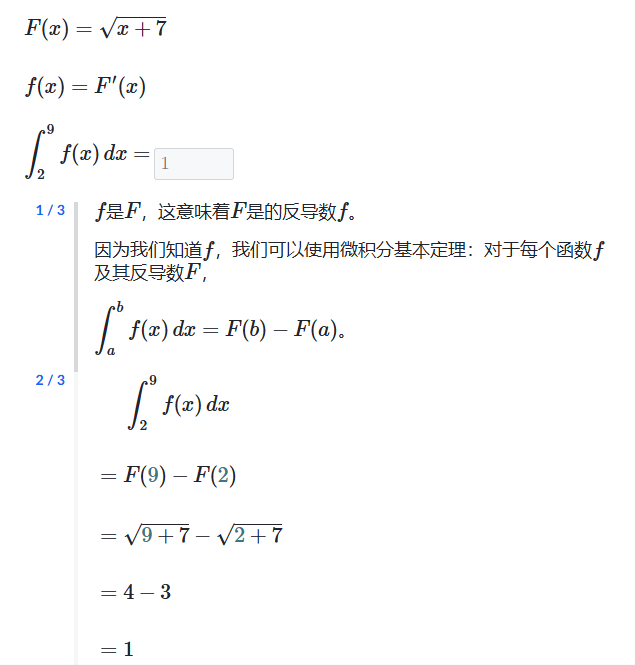
例子:



寻找不定积分和不定积分
基本规则和符号:逆幂规则
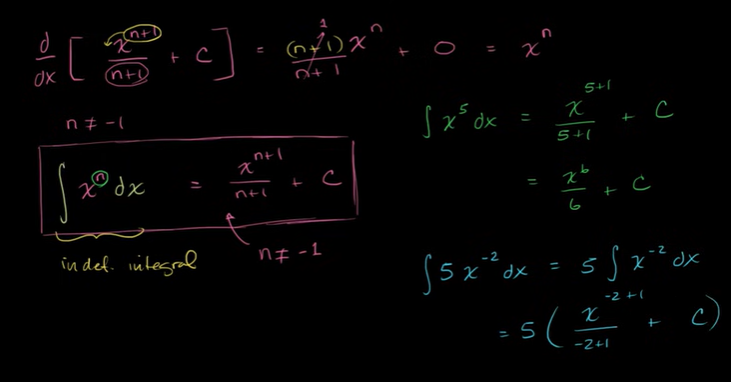
例子:

不定积分:和与倍数
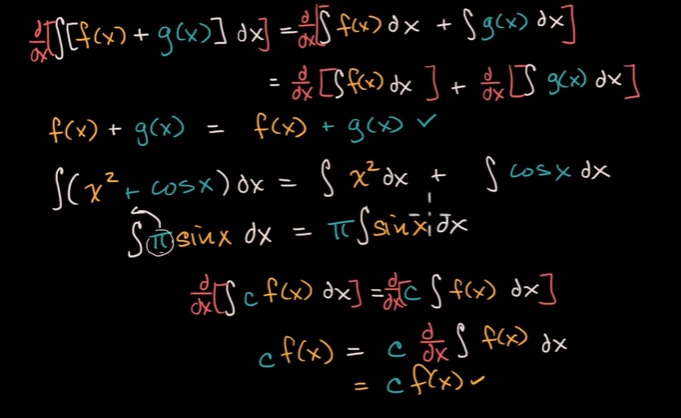
例子:
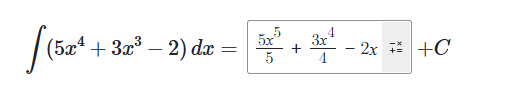
集成之前进行重写
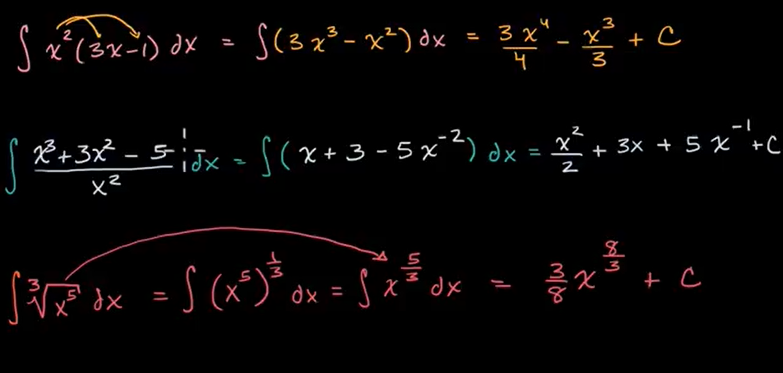

例子:
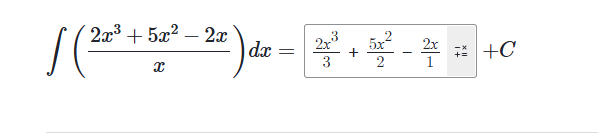
例子:
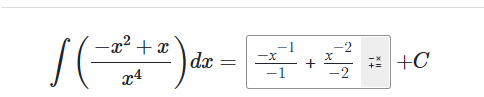






1/x 的不定积分
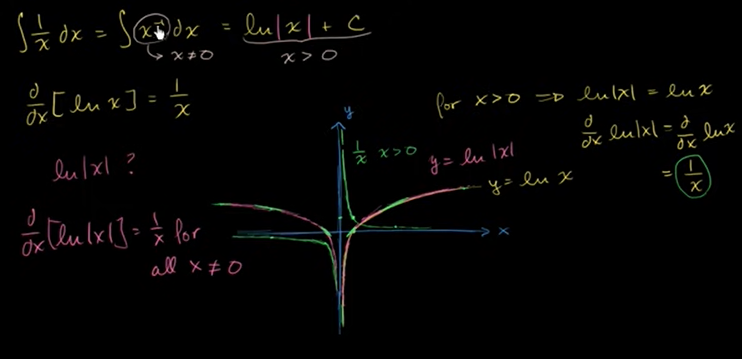
sin(x)、cos(x) 和 eˣ 的不定积分
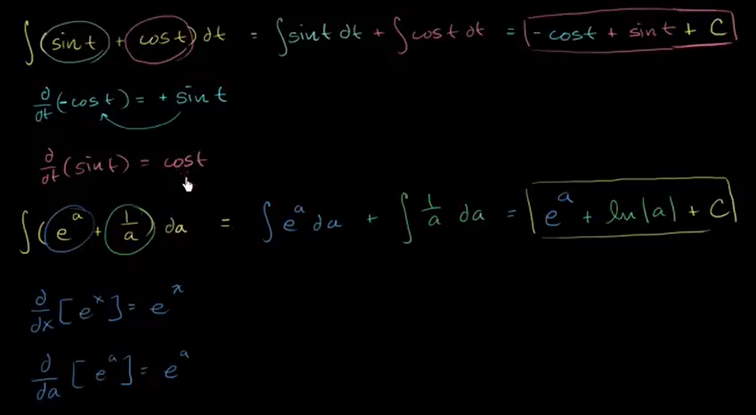
例子:


例子:
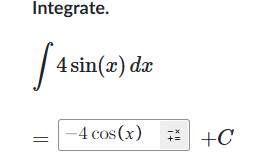

例子:
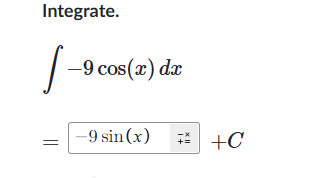


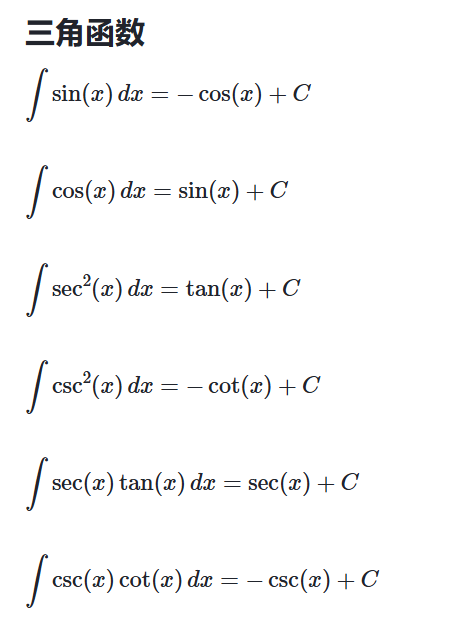


定积分:反幂律
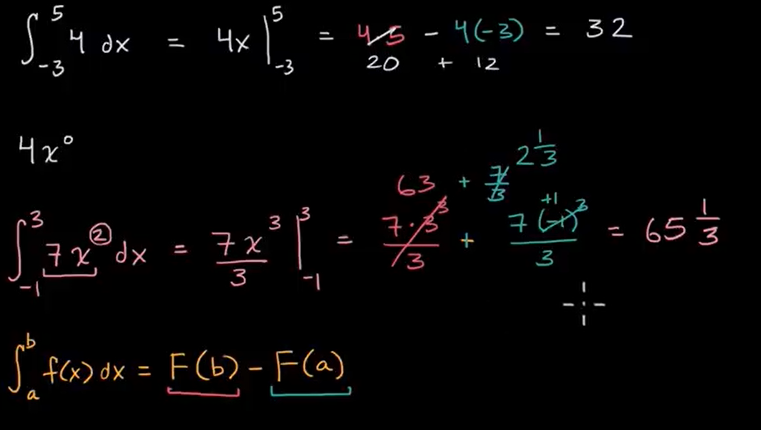
例子:

注意:例子

有理函数的定积分
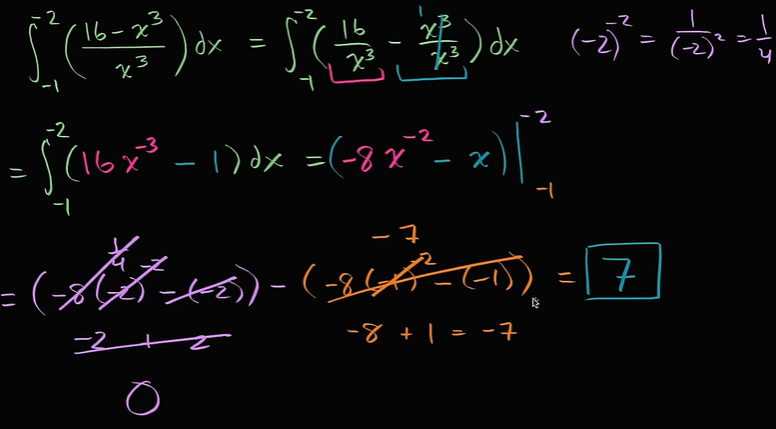
根函数的定积分
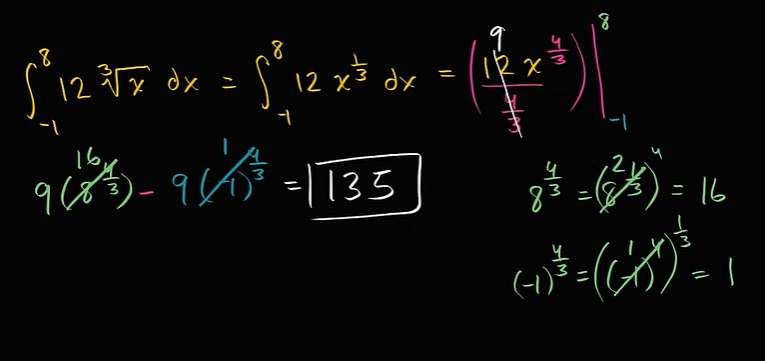
三角函数的定积分
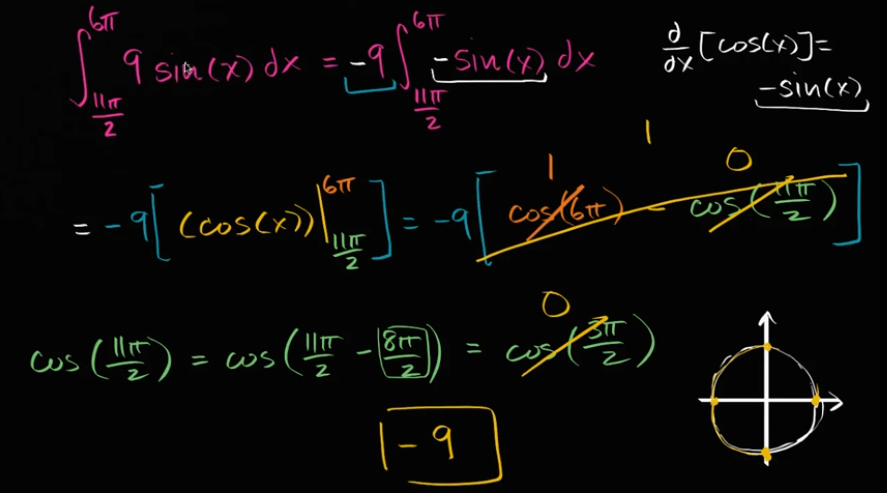
涉及自然对数的定积分
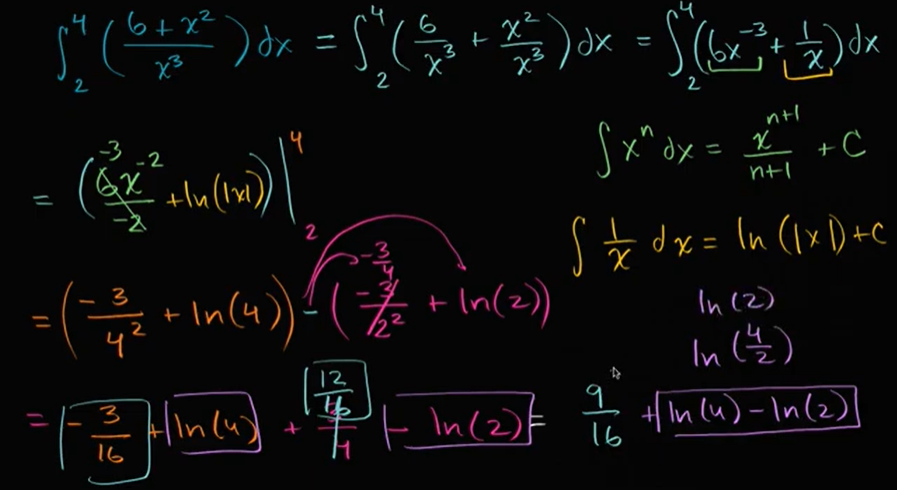
例子:

例子:

分段函数的定积分
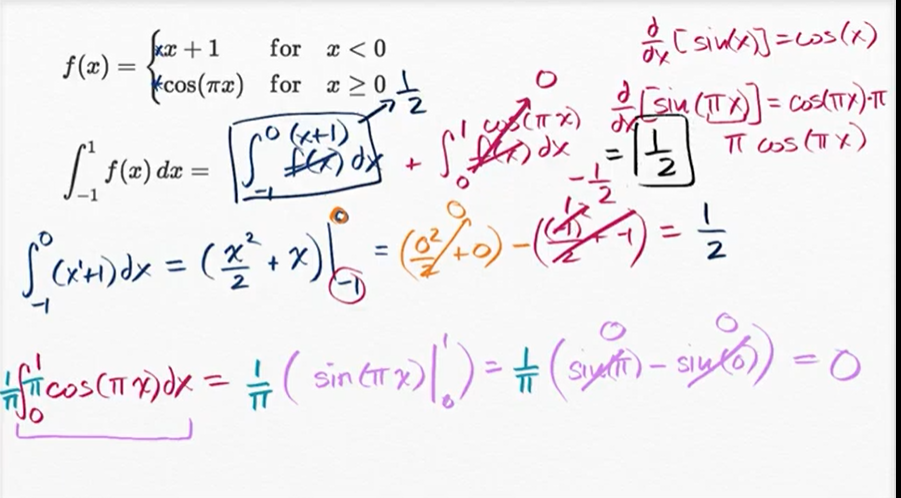
绝对值函数的定积分

例子:
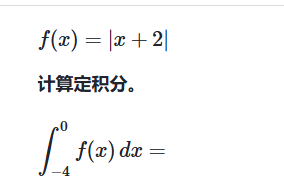



例子:



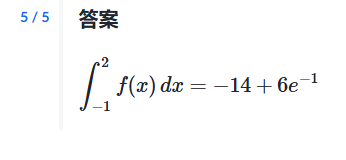
例子:
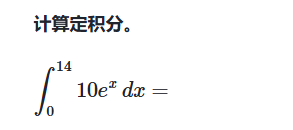

例子:


𝘶 替代介绍
这里面的du是求导后的,而u是没求导之前的,相当于链式求导出来的
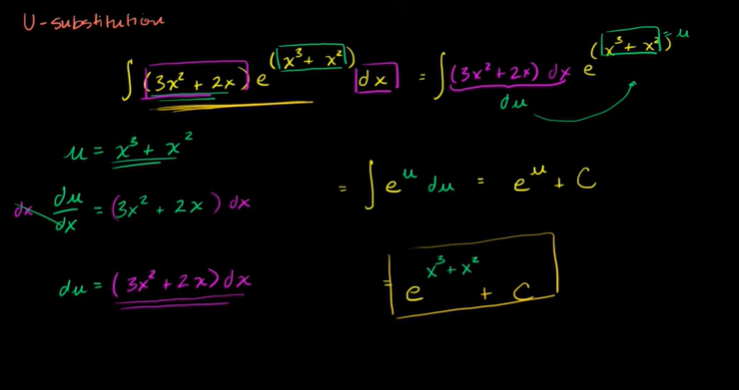


再理解:

𝘶-替换:乘以一个常数
不定积分就是求原来的函数,我们回想一下链式法则,函数7x的导数应该是7的,但是在不定积分变成了1,根号7x+9乘1等于他自己,那么要满足,所以要1/7啊




𝘶-替代:定义𝘶
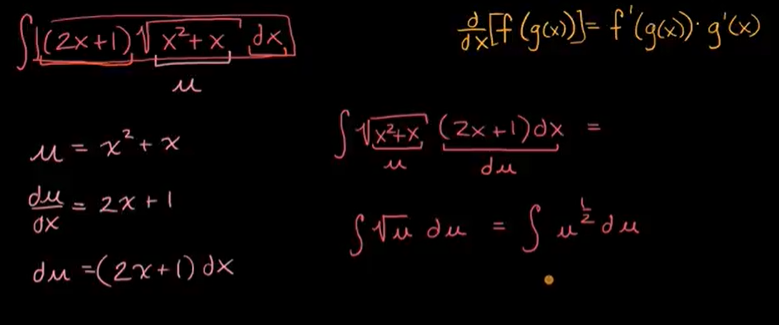
𝘶-替换:定义 𝘶 (更多示例)
u和du都是导数关系
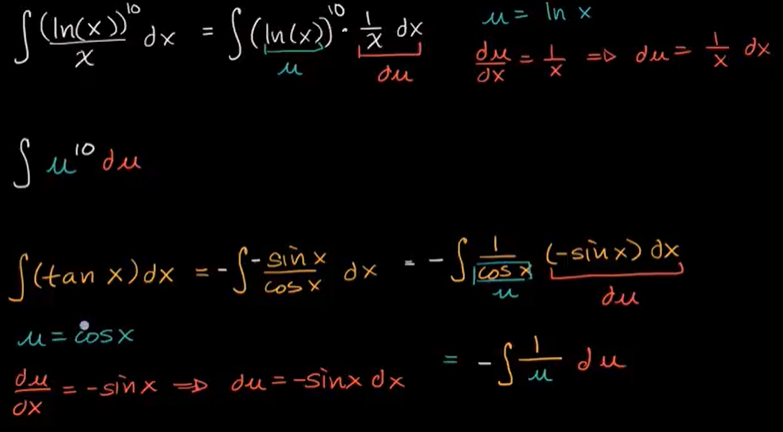

例子:


𝘶-替代:有理函数
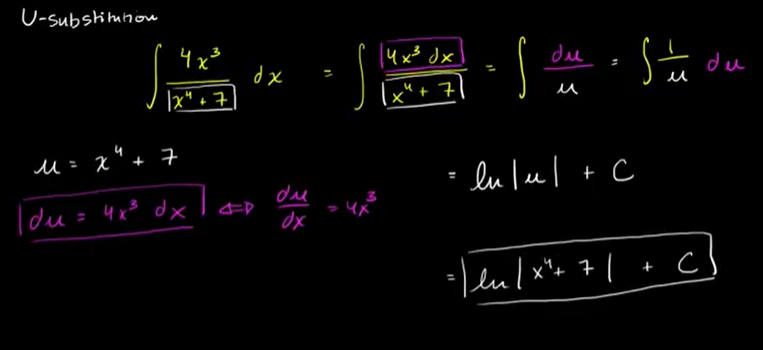
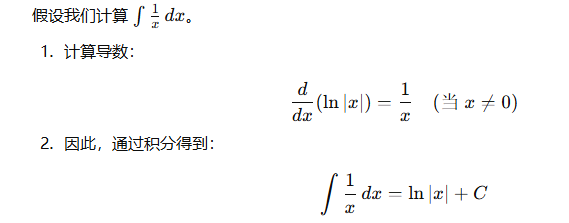
𝘶-替换:对数函数
要留意是不是1/x 和 lnx之间的导数
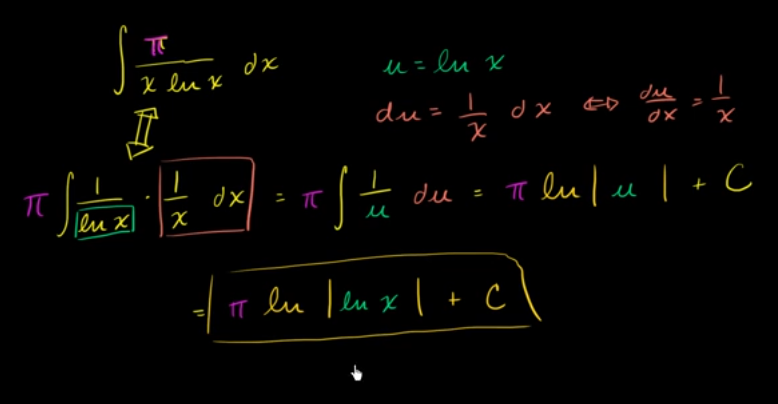

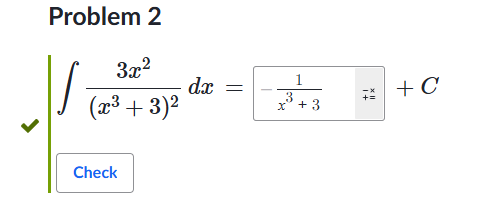



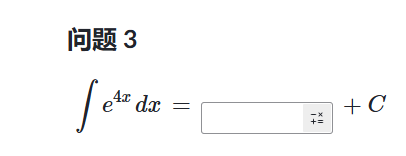


例子:
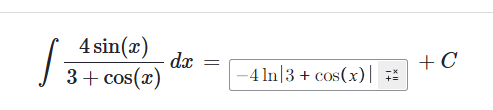


例子:
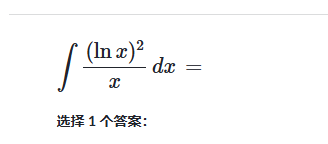

例子:



𝘶-替换:定积分
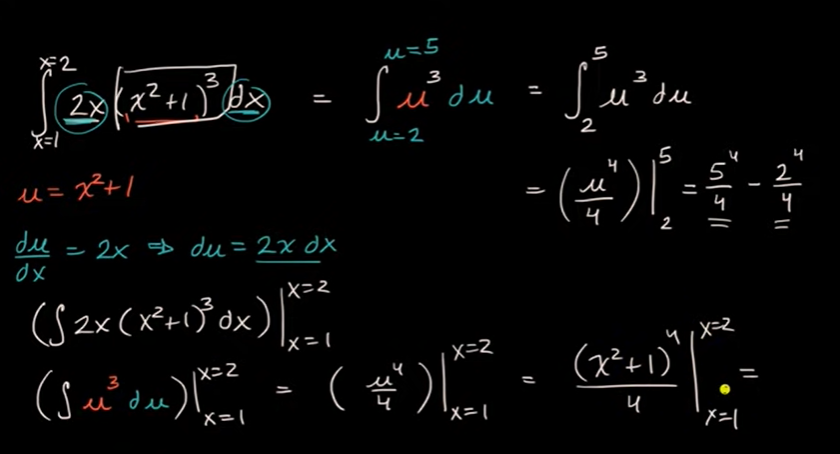

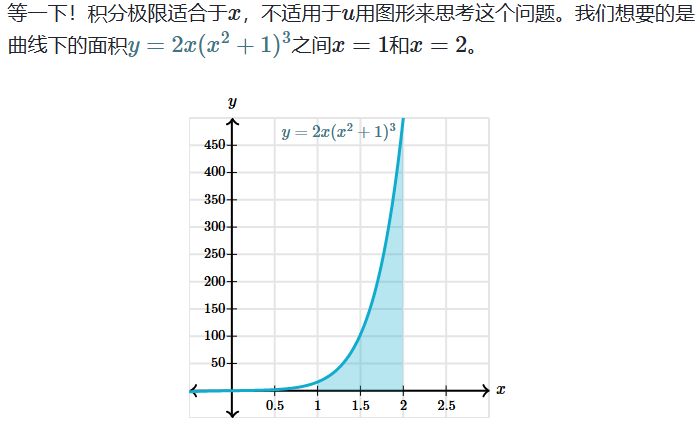
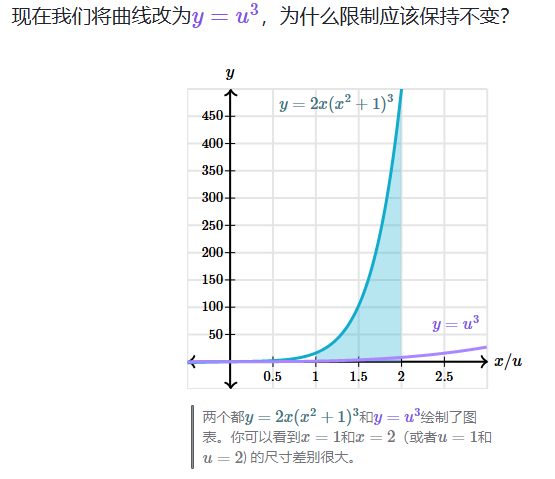

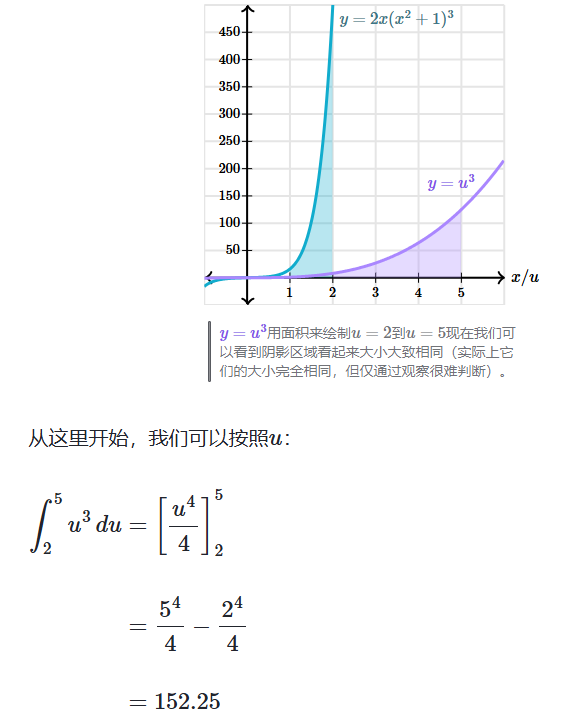
例子:
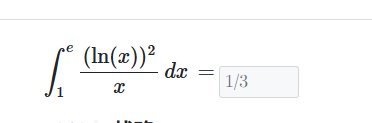


例子:

例子:

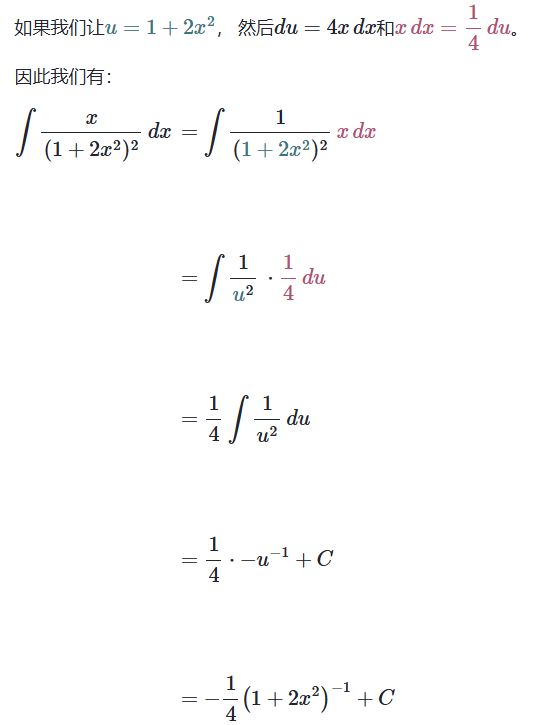

例子:

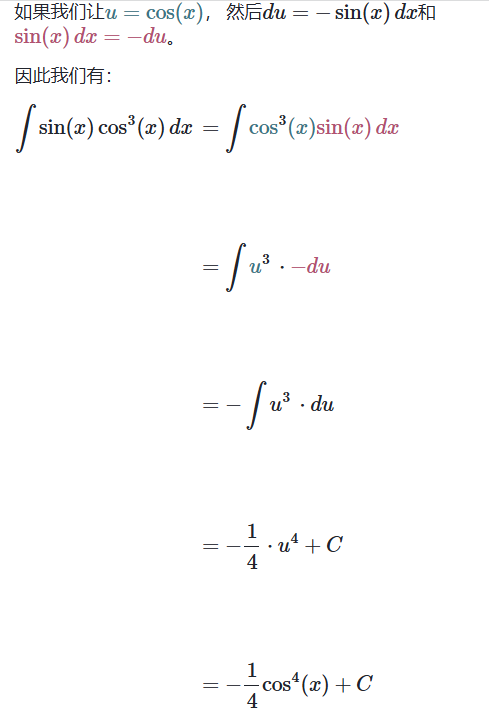

𝘶-替换:指数函数的定积分
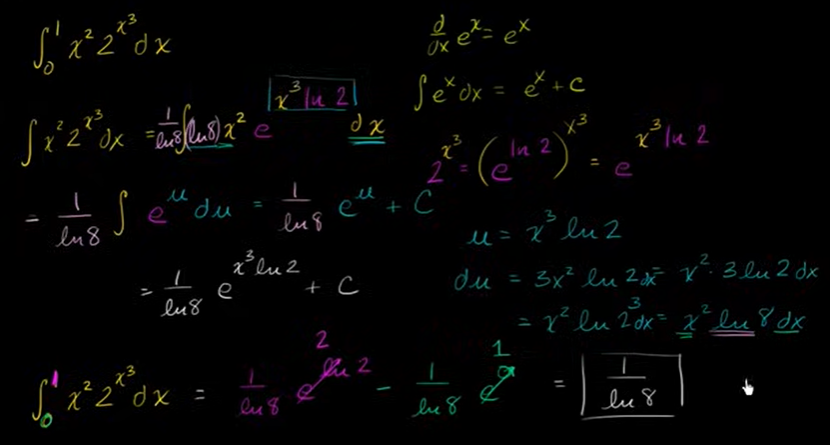
使用长除法进行积分


例子:


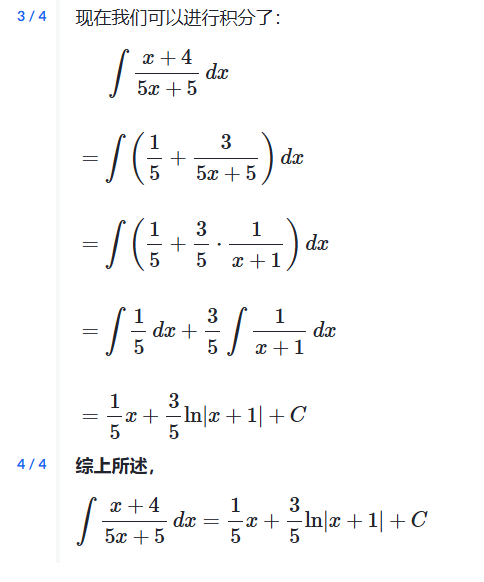
利用完成平方和 arctan(x) 的导数进行积分
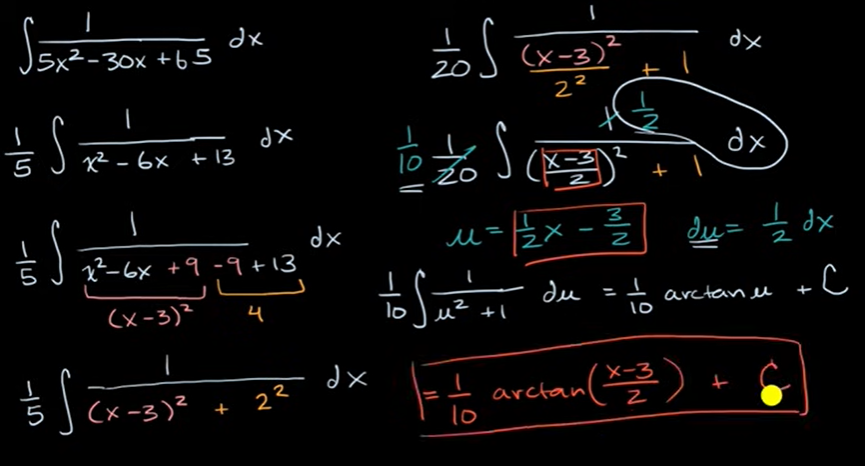





【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 分享一个免费、快速、无限量使用的满血 DeepSeek R1 模型,支持深度思考和联网搜索!
· 基于 Docker 搭建 FRP 内网穿透开源项目(很简单哒)
· ollama系列01:轻松3步本地部署deepseek,普通电脑可用
· 25岁的心里话
· 按钮权限的设计及实现