学习笔记259—低秩分解
目录
概念
1. 奇异值(SVD)分解
2. 张量分解
2.1 CP 分解( Canonical Polyadic Decomposition (CPD)
2.2 TD 分解( Tucker Decomposition )
2.3 BTD 分解(block term decomposition)
概念
本章节涉及到线性代数的知识,磨刀不误砍柴工,理解基本的概念知识是有必要的。该章节的初衷为模型压缩的一个小节,当然在其他领域比如PCA,推荐等都有应用。首先应清楚学习本章的意义,该知识点能够解决什么问题,其后在深入该如何用。后序对低秩的三个子方法浅显的讲解。
1. 秩(Rank)
为了从方程组中去掉多余的方程,引出了“矩阵的秩”。矩阵的秩度量的就是矩阵的行列之间的相关性。为了求矩阵A的秩,我们是通过矩阵初等变换把A化为阶梯型矩阵,若该阶梯型矩阵有r个非零行,那A的秩rank(A)就等于r。 如果矩阵的各行或列是线性无关的,矩阵就是满秩的,也就是秩等于行数。
2. 低秩(Low-Rank)
如果X是一个m行n列的数值矩阵,rank(X)是X的秩,假如rank (X)远小于m和n,则我们称X是低秩矩阵。低秩矩阵每行或每列都可以用其他的行或列线性表出,可见它包含大量的冗余信息。利用这种冗余信息,可以对缺失数据进行恢复,也可以对数据进行特征提取。
3. 低秩分解(Low Rank Filters)
目的:去除冗余,并且减少权值参数
方法:采用两个K*1的卷积核替换掉一个K*K的卷积核(decompose the K convolutions into two separable convolutions of size 1 × K and K × 1)
原理:权值向量主要分布在一些低秩子空间,用少数基来重构权值矩阵
参考: (ICCV 2017) Coordinating Filters for Faster Deep Neural Networks GitHub
4. 矩阵补全(Matrix Completion)
目的:是为了估计矩阵中缺失的部分(不可观察的部分),可以看做是用矩阵X近似矩阵M,然后用X中的元素作为矩阵M中不可观察部分的元素的估计。
5. 矩阵分解(Matrix Factorization)
目的:是指用 A*B 来近似矩阵M,那么 A*B 的元素就可以用于估计M中对应不可见位置的元素值,而A*B可以看做是M的分解,所以称作Matrix Factorization。
这是因为协同过滤本质上是考虑大量用户的偏好信息(协同),来对某一用户的偏好做出预测(过滤),那么当我们把这样的偏好用评分矩阵M表达后,这即等价于用M其他行的已知值(每一行包含一个用户对所有商品的已知评分),来估计并填充某一行的缺失值。若要对所有用户进行预测,便是填充整个矩阵,这是所谓“协同过滤本质是矩阵填充”。
那么,这里的矩阵填充如何来做呢?矩阵分解是一种主流方法。这是因为,协同过滤有一个隐含的重要假设,可简单表述为:如果用户A和用户B同时偏好商品X,那么用户A和用户B对其他商品的偏好性有更大的几率相似。这个假设反映在矩阵M上即是矩阵的低秩。极端情况之一是若所有用户对不同商品的偏好保持一致,那么填充完的M每行应两两相等,即秩为1。
所以这时我们可以对矩阵M进行低秩矩阵分解,用U*V来逼近M,以用于填充——对于用户数为m,商品数为n的情况,M是m*n的矩阵,U是m*r,V是r*n,其中r是人工指定的参数。这里利用M的低秩性,以秩为r的矩阵M’=U*V来近似M,用M’上的元素值来填充M上的缺失值,达到预测效果。
低秩分解主要分为以下三个(SVD分解、Tucker分解、Block Term分解)
1. 奇异值(SVD)分解
论文:A Singularly Valuable Decomposition The SVD of a Matrix
特征值分解和奇异值分解在机器学习领域的方法,让机器学会抽取重要的特征。 可以将一个比较复杂的矩阵用更小更简单的几个子矩阵的相乘来表示,这些小矩阵描述的是矩阵的重要的特性。两者关系紧密,特征值分解和奇异值分解的目的都是一样,就是提取出一个矩阵最重要的特征。区别在于,特征值分解针对方阵而言,奇异值分解可以针对任意矩阵进行分解。循序渐进的首先搞清楚其特征值分解,再理解奇异值分解。这个章节内容建议看看吴军的《数学之美》第十五章节,通过例子讲解了在文本处理中的两个分类问题,通俗易懂。
A. 特征值分解
1. 特征值
如果说一个向量v是方阵A的特征向量,将一定可以表示成下面的形式: ![]() ,这时候λ就被称为特征向量v对应的特征值,一个矩阵的一组特征向量是一组正交向量。特征值分解是将一个矩阵分解成下面的形式:
,这时候λ就被称为特征向量v对应的特征值,一个矩阵的一组特征向量是一组正交向量。特征值分解是将一个矩阵分解成下面的形式:![]() ,其中Q是这个矩阵A的特征向量组成的矩阵,Σ是一个对角阵,每一个对角线上的元素就是一个特征值。这里引用了一些参考文献中的内容来说明一下。首先,要明确的是,一个矩阵其实就是一个线性变换,因为一个矩阵乘以一个向量后得到的向量,其实就相当于将这个向量进行了线性变换。比如说下面的一个矩阵:
,其中Q是这个矩阵A的特征向量组成的矩阵,Σ是一个对角阵,每一个对角线上的元素就是一个特征值。这里引用了一些参考文献中的内容来说明一下。首先,要明确的是,一个矩阵其实就是一个线性变换,因为一个矩阵乘以一个向量后得到的向量,其实就相当于将这个向量进行了线性变换。比如说下面的一个矩阵:  ,它其实对应的线性变换是下面的形式:
,它其实对应的线性变换是下面的形式: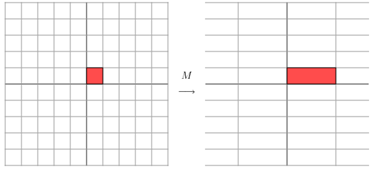
因为这个矩阵M乘以一个向量(x,y)的结果是: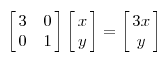 ,该矩阵是对称的,所以这个变换是一个对x,y轴的方向一个拉伸变换(每一个对角线上的元素将会对一个维度进行拉伸变换,当值>1时,是拉长,当值<1时时缩短),当矩阵不是对称的时候,假如说矩阵是下面的样子:
,该矩阵是对称的,所以这个变换是一个对x,y轴的方向一个拉伸变换(每一个对角线上的元素将会对一个维度进行拉伸变换,当值>1时,是拉长,当值<1时时缩短),当矩阵不是对称的时候,假如说矩阵是下面的样子:
它所描述的变换是下面的样子: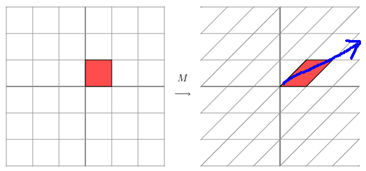
这其实是在平面上对一个轴进行的拉伸变换(如蓝色的箭头所示),在图中,蓝色的箭头是一个最主要的变化方向(变化方向可能有不止一个),如果我们想要描述好一个变换,那我们就描述好这个变换主要的变化方向就好了。反过头来看看之前特征值分解的式子,分解得到的Σ矩阵是一个对角阵,里面的特征值是由大到小排列的,这些特征值所对应的特征向量就是描述这个矩阵变化方向(从主要的变化到次要的变化排列)。
当矩阵是高维的情况下,那么这个矩阵就是高维空间下的一个线性变换,这个线性变化可能没法通过图片来表示,但是可以想象,这个变换也同样有很多的变换方向,我们通过特征值分解得到的前N个特征向量,那么就对应了这个矩阵最主要的N个变化方向。我们利用这前N个变化方向,就可以近似这个矩阵(变换)。也就是之前说的:提取这个矩阵最重要的特征。总结一下,特征值分解可以得到特征值与特征向量,特征值表示的是这个特征到底有多重要,而特征向量表示这个特征是什么,可以将每一个特征向量理解为一个线性的子空间,我们可以利用这些线性的子空间干很多的事情。不过,特征值分解也有很多的局限,比如说变换的矩阵必须是方阵。
2. 正交矩阵
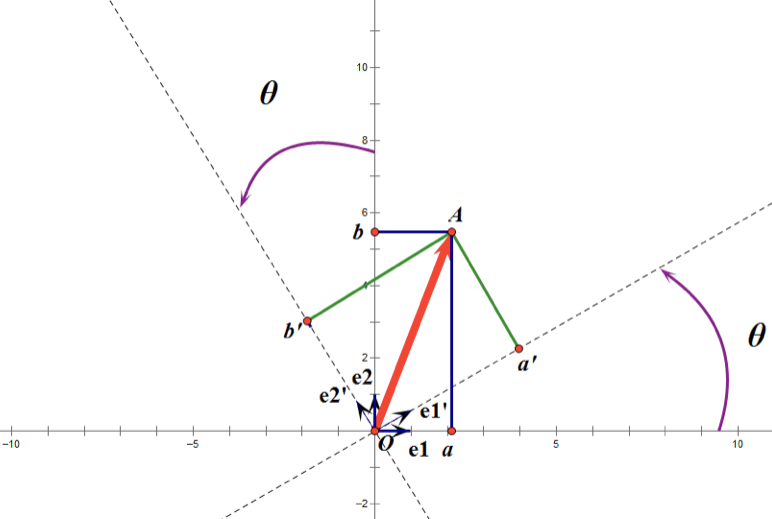
正交矩阵是在欧几里得空间里的叫法,在酉空间里叫酉矩阵,一个正交矩阵对应的变换叫正交变换,这个变换的特点是不改变向量的尺寸和向量间的夹角。下图是一个直观的认识:
假设二维空间中的向量OA,它在标准坐标系(也就是e1和e2表示的坐标系)中的表示为(a,b)’(‘表示转置);现在用另一组坐标e1’、e2’表示为(a’,b’)’;那么存在矩阵U使得(a’,b’)’=U(a,b)’,而矩阵U就是正交矩阵。
通过上图可知,正交变换只是将变换向量用另一组正交基来表示,在这个过程中并没有罪向量作拉伸,也不改变向量的空间位置,对两个向量同时做正交变换,变换的前后两个向量的夹角显然也不会改变。上图是一个旋转的正交变换,可以把e1’、e2’坐标系看做是e1、e2坐标系经过旋转某个θ角度得到,具体的旋转规则如下:
a’和b’实际上是x在e1’和e2’轴上投影的大小,所以直接做内积可得:
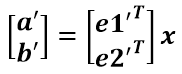
从图中可以看到:
所以:
正交矩阵U的行(列)之间都是单位正交向量,它对向量做旋转变换。这里解释一下:旋转是相对的,就那上面的图来说,我们可以说向量的空间位置没有变,标准参考系向左旋转了θ角度,而如果我选择了e1’、e2’作为新的标准坐标系,那么在新坐标系中OA(原标准坐标系的表示)就变成了OA’,这样看来就好像坐标系不动,把OA往顺时针方向旋转了θ角度,这个操作实现起来很简单:将变换后的向量坐标仍然表示在当前坐标系中。 正交变换的另一个方面是反射变换,也即e1’的方向与图中方向相反。
总结:正交矩阵的行(列)向量都是两两正交的单位向量,正交矩阵对应的变换为正交变换,它有两种表现:旋转和反射。正交矩阵将标准正交基映射为标准正交基(即图中从e1、e2到e1’、e2’)。
3. 特征值分解(EVD)
在讨论SVD之前,先了解矩阵的特征值分解(EVD),这里选择特殊的矩阵——对角阵,对称矩阵又一个性质就是总能相似对角化,对称矩阵不同特征值对应的特征向量两两正交。一个矩阵能能相似对角化即说明其特征子空间即为其列空间,若不能对角化则其特征子空间为列空间的子空间。现在假设存在m * m的满秩对称矩阵A,它有m个不同的特征值,设特征值为: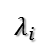
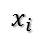
进而:
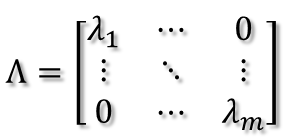
所以可得到A的特征值分解(由于对称阵特征向量两两正交,所以U为正交阵,正交阵的逆矩阵等于其转置):
这里假设A有m个不同的特征值,实际上,只要A是对称阵其均有如上分解。
矩阵A分解了,相应的,其对应的映射也分解为三个映射。现在假设有x向量,用A将其变换到A的列空间中,那么首先由UT先对x做变换:
U是正交阵UT也是正交阵,所以UT对x的变换是正交变换,它将x用新的坐标系来表示,这个坐标系就是A的所有正交的特征向量构成的坐标系。比如将x用A的所有特征向量表示为:
则通过第一个变换就可以把x表示为[a1 a2 … am]T:
紧接着,在新的坐标系表示下,由中间那个对角矩阵对新的向量坐标换,其结果就是将向量往各个轴方向拉伸或压缩:
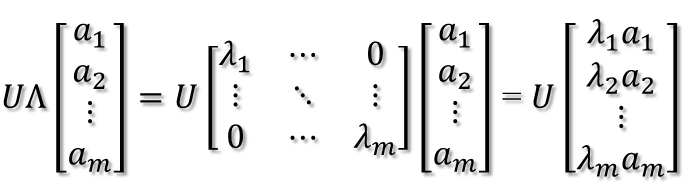
从上图可以看到,如果A不是满秩的话,那么就是说对角阵的对角线上元素存在0,这时候就会导致维度退化,这样就会使映射后的向量落入m维空间的子空间中。
最后一个变换就是U对拉伸或压缩后的向量做变换,由于U和UT是互为逆矩阵,所以U变换是UT变换的逆变换。
因此,从对称阵的分解对应的映射分解来分析一个矩阵的变换特点是非常直观的。假设对称阵特征值全为1那么显然它就是单位阵,如果对称阵的特征值有个别是0其他全是1,那么它就是一个正交投影矩阵,它将m维向量投影到它的列空间中。
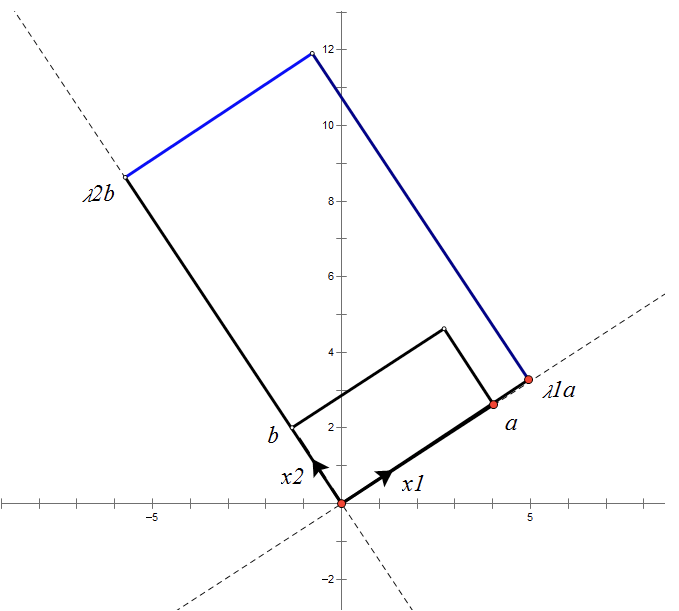
根据对称阵A的特征向量,如果A是2 * 2的,那么就可以在二维平面中找到这样一个矩形,是的这个矩形经过A变换后还是矩形:
这个矩形的选择就是让其边都落在A的特征向量方向上,如果选择其他矩形的话变换后的图形就不是矩形了!
B. 奇异值分解
1. 奇异值
特征值分解是提取矩阵特征不错的方法,但局限在于只针对方阵。奇异值分解可以解决任意矩阵的分解。
![]()
假设A是一个M * N的矩阵,那么得到的U是一个M * M的方阵(里面的向量是正交的,U里面的向量称为左奇异向量),Σ是一个M * N的矩阵(除了对角线的元素都是0,对角线上的元素称为奇异值),V’(V的转置)是一个N * N的矩阵,里面的向量也是正交的,V里面的向量称为右奇异向量),从图片来反映几个相乘的矩阵的大小可得下面的图片: 
那么矩阵A的奇异值和方阵的特征值是如何对应的?
我们将一个矩阵AT * A,将会得到一个方阵,我们用这个方阵求特征值可以得到:
![]()
这里得到的Vi就是上面的右奇异向量,此外,我们可以得到:

这里的σi就是上面说的奇异值。ui就是上面的左奇异向量。奇异值σ跟特征值相似,在矩阵Σ中也是按从大到小的方式排列,而且σ的值减小的特别的快,在很多的情况下前10%甚至1%的奇异值之和就占了全部奇异值之和的99%以上。也就是说可以用前r个大的奇异值来近似的描述矩阵,这里定义奇异值的分解: ![]()
r是一个远远小于m和n的值,矩阵的乘法看起来是这个样子:
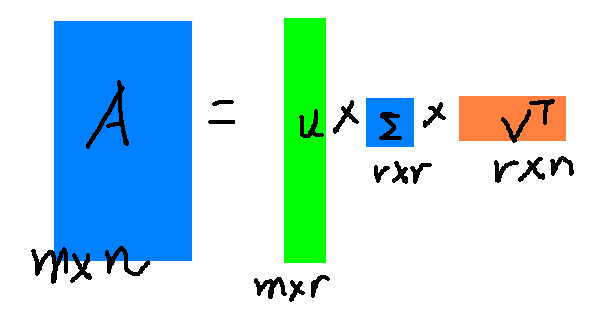
右边的三个矩阵相乘的结果将会是一个接近于A的矩阵,在这儿,r越接近于n,则相乘的结果越接近于A。而这三个矩阵的面积之和(在存储观点来说,矩阵面积越小,存储量就越小)要远远小于原始的矩阵A,我们如果想要压缩空间来表示原矩阵A,我们存下这里的三个矩阵:U、Σ、V就好了。
2. 奇异值分解 SVD
上面的特征值分解的A矩阵是对称阵,根据EVD可以找到一个(超)矩形使得变换后还是(超)矩形,也即A可以将一组正交基映射到另一组正交基!那么现在来分析:对任意M*N的矩阵,能否找到一组正交基使得经过它变换后还是正交基?答案是肯定的,它就是SVD分解的精髓所在。
现在假设存在M*N矩阵A,事实上,A矩阵将n维空间中的向量映射到k(k<=m)维空间中,k=Rank(A)。现在的目标就是:在n维空间中找一组正交基,使得经过A变换后还是正交的。假设已经找到这样一组正交基:
{v1,v2,v3,…,vn}
则A矩阵将这组基映射为:
{Av1,Av2,Av3,…,Avn}
如果要使他们两两正交,即:
Avi · Avj = (Avi)TAvj = viTATAvj = 0
根据假设,存在:
viTvj = vivj = 0
所以如果正交基v选择为ATA的特征向量的话,由于ATA是对称阵,v之间两两正交,那么: 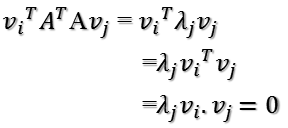
这样就找到了正交基使其映射后还是正交基了,现在,将映射后的正交基单位化,因为:
所以有:
所以取单位向量:
当k < i <= m时,对u1,u2,…,uk进行扩展u(k+1),…,um,使得u1,u2,…,um为m维空间中的一组正交基,即将{u1,u2,…,uk}正交基扩展成{u1,u2,…,um}Rm空间的单位正交基,同样的,对v1,v2,…,vk进行扩展v(k+1),…,vn(这n-k个向量存在于A的零空间中,即Ax=0的解空间的基),使得v1,v2,…,vn为n维空间中的一组正交基,即:
在A的零空间中选择{vk+1,vk+2,…,vn}使得AvI = 0,i > k并取σ = 0则可得到:
继而得到A矩阵的奇异值分解:
V是n*n的正交矩阵,U是m*m的正交矩阵,Σ是m*n的对角阵
现在可以来对A矩阵的映射过程进行分析了:如果在n维空间中找到一个(超)矩形,其边都落在ATA的特征向量的方向上,那么经过A变换后的形状仍然为(超)矩形!
vi为ATA的特征向量,称为A的右奇异向量,ui=Avi实际上为AAT的特征向量,称为A的左奇异向量。下面利用SVD证明文章一开始的满秩分解:
利用矩阵分块乘法展开得:
可以看到第二项为0,有:
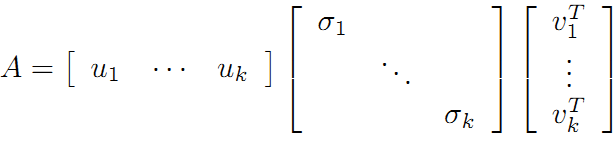
令:
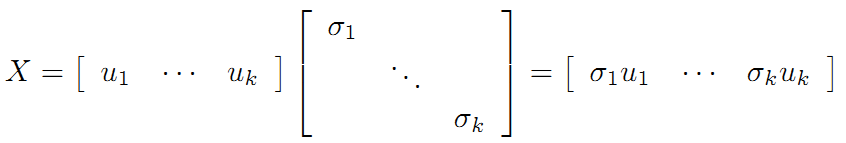
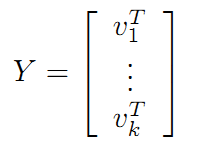
在《数学之美》上面有验证U、V都是酉矩阵。
则A=XY即是A的满秩分解。
2. 张量(Tucker)分解
张量:一般一维数组,我们称之为向量(vector),二维数组,我们称之为矩阵(matrix);三维数组以及多位数组,我们称之为张量(tensor)。 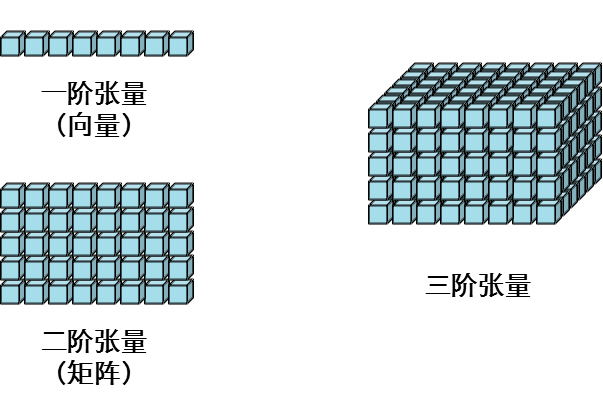
张量的知识点可参看大佬博客:张量
2.1 CP 分解( Canonical Polyadic Decomposition (CPD)
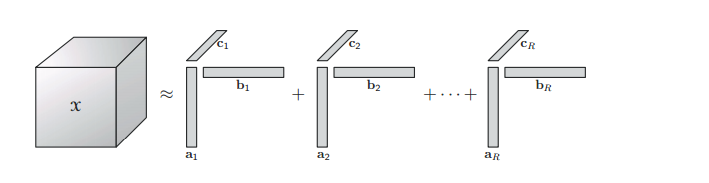
CP分解的知识点可参看大佬博客:CP分解
2.2 TD 分解( Tucker Decomposition )
Tucker分解是一种高阶的主成分分析,它将一个张量表示成一个核心(core)张量沿每一个mode乘上一个矩阵。
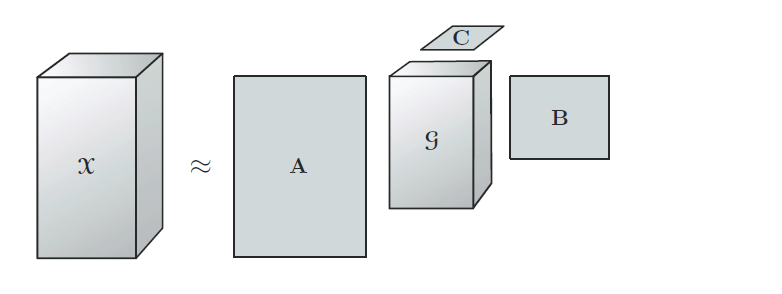
内容可参看大佬博客:张量分解-Tucker分解
2.3 BTD 分解(block term decomposition)
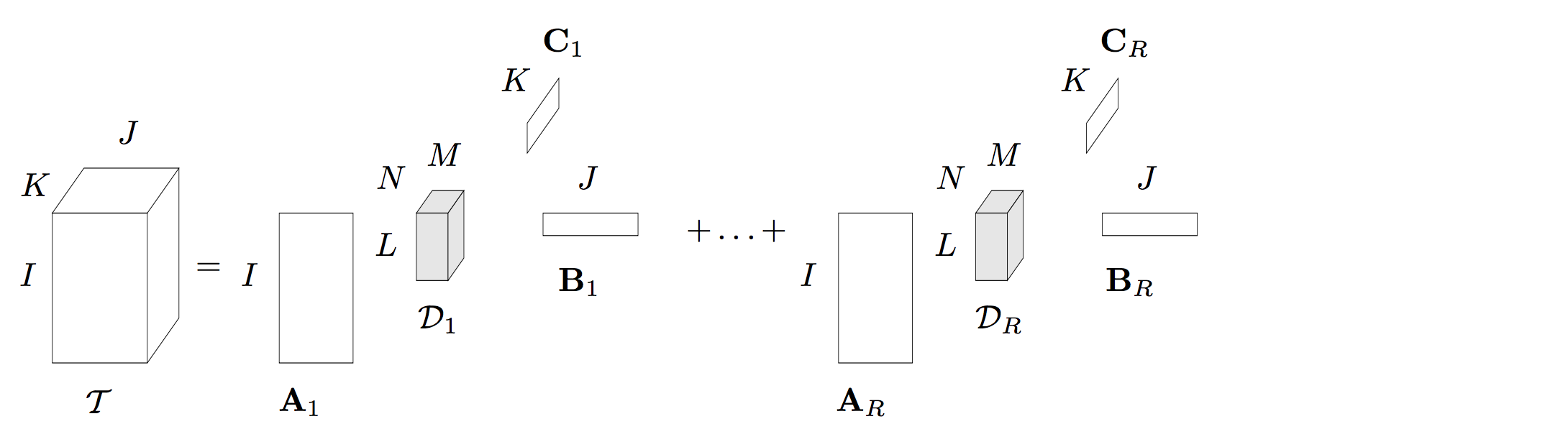
BTD的内容可参考大佬博客:BTD分解
总结:低秩逼近的方法用于全连接层效果较好,但是对运行时间提升空间不是很大。一般能达到1.5倍。将低秩逼近的压缩算法用于卷积层时,会出现误差累积的效果,对最后精度损失影像较大,需要对网络进行逐层的微调,费时费力。





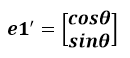
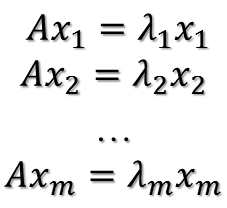
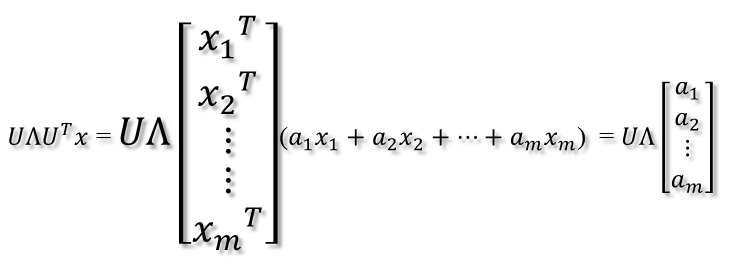
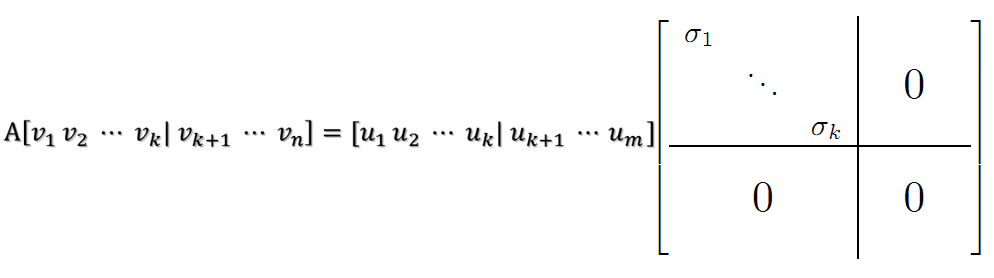
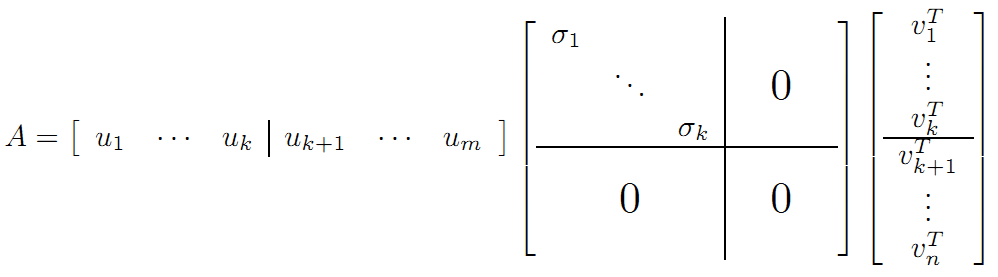
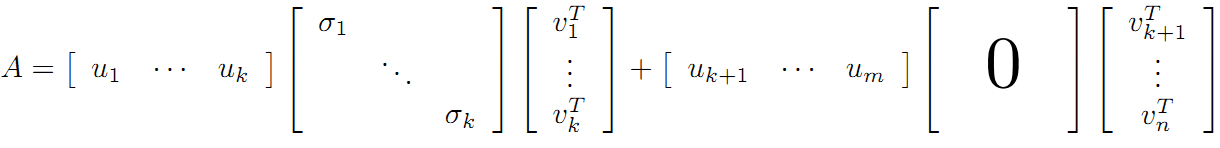


【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 分享4款.NET开源、免费、实用的商城系统
· 全程不用写代码,我用AI程序员写了一个飞机大战
· MongoDB 8.0这个新功能碉堡了,比商业数据库还牛
· 白话解读 Dapr 1.15:你的「微服务管家」又秀新绝活了
· 上周热点回顾(2.24-3.2)