概率机器人-第二章 递归状态估计
概率机器人技术的核心就是通过传感器数据来估计状态的思路。
状态估计解决的是从不能直接观测但可以推断的传感器数据中估计数量的问题。
状态估计旨在从数据中找回状态变量。
概率状态估计算法在可能的状态空间上计算置信度分布。
基本概率概念-->机器人环境相互作用的形式化模型-->贝叶斯滤波(状态估计的递归算法)-->实现贝叶斯滤波的表示和计算问题
概率基本概念:
随机变量:传感器测量、控制、机器人的状态及其环境;
如:抛硬币 p(X=x) , 表示:随机变量X具有x值的概率。
具体的:硬币 p( X = head ) = p( X = tail ) = 1/2
离散概率和为1:
![]()
概率永远为非负值,即:p( X = x ) >= 0
本书大部分技术都是在连续空间提出估计和制定决策。
连续空间的特点是随机变量可以取连续值。
本书中假定的所有连续随机变量都拥有概率密度函数(Probability Density Function,PDF)。
普通的密度函数是具有均值μ和方差σ2的一维正态分布(normal distribution),用高斯函数表示如下:
![]() (2.3)
(2.3)
通常可以缩写为:
![]()

当x为标量,Σ=σ2时,两个式子是等效的。
正如离散概率分布总和为1,一个概率密度函数的积分也总是为1: ∫ p(x)dx = 1 ;
需注意:与离散概率不同,概率密度函数上限不局限于1。
关键字:概率、概率密度、概率密度函数
两个随机变量X和Y的联合分布(joint distribution):p( x,y ) = p( X = x,Y = y )
如果X和Y相对独立: p( x,y ) = p( x )p( y )
条件概率(conditional probability):
X的概率表示为: p(x | y) = p(X = x | Y = y) , 已知Y的值是y。
若 p(y) > 0 , 则条件概率定义为:
![]()
若X和Y相互独立,则有:
![]()
全概率定理:
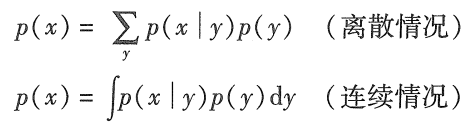
贝叶斯准则:
 (2.4)
(2.4)
贝叶斯准则在概率机器人中起到主导作用,
假定x是由y推测出来的数值,则概率p(x)称为先验概率分布(priorprobability distribution);
其中,y是数据,即:传感器的测量值;
概率p(x|y)称为在X上的后验概率分布(posterior probability distribution);
上式2.4中,贝叶斯准则利用了“逆”条件概率p(y|x)和先验概率p(x),计算得出后验概率p(x|y)。
在机器人学中,概率p(y|x)通常是生成模型(generative model),一般的,在抽象层面上,表示状态变量X如何引起检测数据Y。
贝叶斯归一化表示方式: p(x|y) = ηp(y|x)p(x)
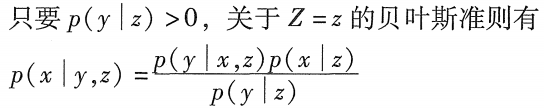

机器人环境交互
环境或世界是拥有内部状态的动态系统;
机器人也可以通过执行机构影响环境,每一个控制行为都会影响环境的状态,并对机器人状态的内部置信度有影响。
状态
环境特征以状态来表征;
本书认为,状态是所有会对未来产生影响的机器人及其环境的所有方面的因素;
状态分为:静态和动态;
环境交互
环境传感器测量
感知交互的结果叫测量、观察或认知;
控制动作改变世界的状态;
环境测量数据提供了环境的暂态信息;
控制数据携带环境中关于状态改变的信息;
概率生成法则
状态和测量的演变由概率法则支配;
状态转移概率和测量概率一起描述机器人及其环境组成的动态随机系统。
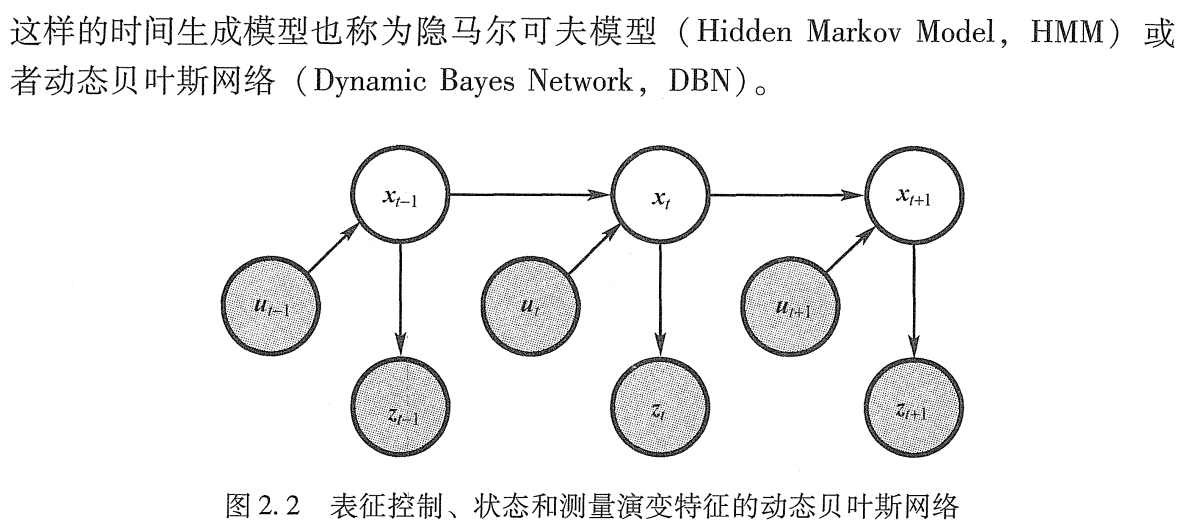
下图中,动态贝叶斯网络显示了由这些概率定义的状态和测最的演变;
时刻 t 的状态随机地依赖 t -1 时刻的状态和控制 ut。测量 zt 随机地依赖时刻 t 的状态。
置信分布
置信度反映了机器人有关环境状态的内部信息;
概率机器人通过条件概率分布表示置信度;
置信度分布是:可以获得数据条件的关于状态变量的后验概率,表示为:
![]()
在概率滤波的框架下,该概率经常被称为预测(prediction);
贝叶斯滤波
贝叶斯滤波算法
大多数计算置信度的通用算法都是由贝叶斯滤波(Bayes filter)算法给出的;


总之,贝叶斯滤波算法以到时间 t 的测量和控制数据为条件来计算状态 xt 的后验。推导假设世界是马尔可夫的,也就是状态是完整的。
贝叶斯滤波算法的任何具体实现都需要三个概率分布:初始置信度、测量概率和状态转移概率。
马尔可夫假设(Markov assumption)或者完整状态假设(complete state assumption)
表示法和计算
需要权衡的特性:1计算效率;2近似的精度;3易于实施。



