完全二叉树的性质
完全二叉树的性质
定义
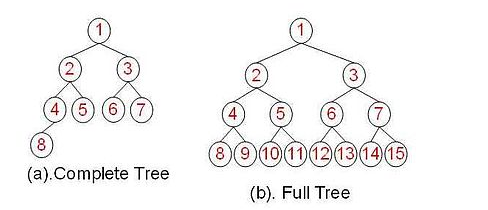
- 满二叉树
-
一棵深度为k，且有 $2^{k+1}-1$ 个节点的二叉树，称为满二叉树（Full Binary Tree）。 这种树的特点是每一层上的节点数都是最大节点数。 - 完全二叉树
-
而在一棵二叉树中，除最后一层外，若其余层都是满的，并且最后一层或者是满的，或者是在右边缺少连续若干节点，则此二叉树为完全二叉树（Complete Binary Tree）。 - 高度（深度）
-
即层数k，注意【根】定义为$height(root)=0$。
性质
- 具有n个节点的完全二叉树的深度为 \(k=log_{2}n\) 。
- 【满二叉树】\(i\)层的节点数目为：\(2^i\)
- 【满二叉树】节点总数和深度的关系：\(n=\sum_{i=0}^{k}2^i = 2^{k+1}-1\)
- 【完全二叉树】最后一层的节点数为：\(n-(2^k - 1) = n + 1 -2^k\) （因为除最后一层外，为【满二叉树】）
- 【完全二叉树】左子树的节点数为（总节点为n）：
\[l(n) = \begin{cases} n-2^{k-1}, & n+1-2^k \le 2^{k-1} \text{ 因为最后一层全部都在左子树，右子树为【满二叉树】高度为 k-2}\\
2^{k}-1, & n+1-2^k \gt 2^{k-1} \text{ 因为左子树为满二叉树，高度为k-1} \end{cases}
\]
- 【完全二叉树】右子树： \(r(n) = n-l(n)\)
