扫描线算法
扫描线算法
给出几个矩形对角端点坐标，求这些矩形整体覆盖的面积。
基本思想如下图：
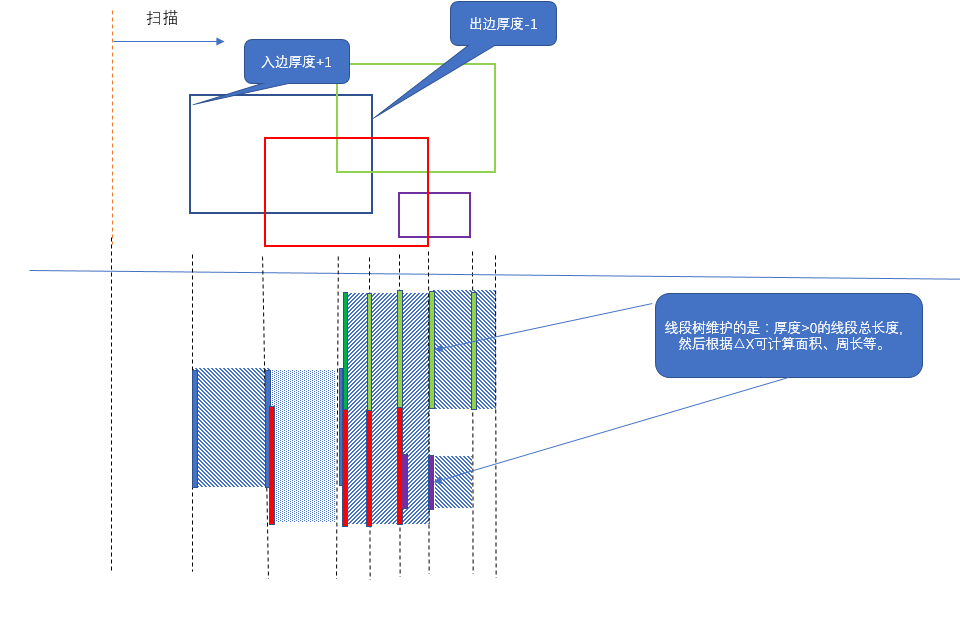
- 先离散化。
- 【扫描线】是一根想象中的虚线，从左往右扫描，遇到【矩形】则成为【事件】。
- 遇到【起始边】，则
Update相应区间的【厚度】或者【覆盖次数】CoverCnt+1。 - 遇到【结束边】，则
Update相应区间的【厚度】CoverCnt-1。 - 用【线段树】维护【区间】的厚度CovertCnt，以及区间CovertCnt > 0 的线段的总长度Len。
求面积poj1511
求面积比较简单：
\[S = \Delta x * \sum_{cnt\gt 0}(raw(i+1)-raw(i))
\]
即可。也就是每次Update后，增加面积即可。
如何处理CovertCnt的不一致？
CovertCnt不一致，出现在“断点”，即Update后，区间不连续。比如： Range[1-4].CovertCnt=2,现在Update(R[1-2]), 如何处理？
- 标记为【无效】，查询时，如果有【无效标记】，则继续往下查。
- 干脆直接维护SumLen,出现这种情况，由下往上PushUp更新SumLen即可。
从本质上来讲，两者效果差不多，一个是马上维护SumLen，一个是查询时再计算SumLen。后者省了一次函数调用，和有可能再次被“全区间覆盖”时简化计算，效率能够高一些。所以熟悉哪种就用哪种，切记切记，会10种不如精一种！
Query时需要pushdown吗？
因为查询的是整个区间，不存在“交叉区间”，所以不需要。（当然PushDown【没毛病】，如果没有十足的把握，还是PushDown，反正没有什么副作用。）
Query，当【查询区间】和【更新区间】出现【交叉】的时候，需要
PushDown，比如：更新到：[1-2]和[3-4]但要查询[2-3]，则只能由[2]``[3]两部分构成，所以你必须要从[1-2]PushDown到[2],从[3-4]pushdown到[3]。但如果永远查询都是[1-N]的话，就不存在这种情况。
求周长 hdu1828
道理基本上差不多，稍复杂。
- 两次扫描，横向和竖向。
- 每次
Update后，【周长的增加额】 = abs(【Update前SumLen】-【SumLen】)
\[ \Delta L_i= \sum_{cnt\gt 0}(raw(i+1)-raw(i)) \\
\Delta L = \sum_{i=0}^nAbs(\Delta L_i -\Delta L_{i-1} )
\]
当然也有【一次】扫描的方法，不过需要维护更多的参数，更加复杂一些。一般情况下没有必要。
