【数组】 差分
【数组】 差分
前缀和 与 差分
我在前面的两篇博客里面简要介绍了一下一维、二维数组的前缀和的一些知识点，提到前缀和，那很自然地就会提到差分的概念。
首先我们回顾一下前缀和：原数组a[n]和依据原数组构造出的新数组s[n]，s[n]是a[n]的前缀和数组。
俗话说，有来有往，阴阳交汇，分久必合、合久必分......
总而言之，我们看到了新数组s[n]是原数组a[n]的前缀和数组，但我们都知道，事物之间的影响总是交互的，所以我们必然会想到原数组a[n]是新数组s[n]的什么？只是前缀和数组的原数组吗？
现在让我们先把注意力投向求前缀和数组的公式：
s[n] = s[n-1] + a[n];
现在让我们抛开s[n]相对于a[n]前缀和的身份不谈，我们有一个普通s[n]，它的每一项s[n]都基于上一向s[n-1]的值 再加上一个常数a[n]。
这个常数a[n]正是数组s[n]与s[n-1]的差值。
那么我们变换公式：a[n] = s[n] - s[n-1]。
由此我们得到一个新但旧的数组即原数组，a[n]，称为s[n]数组的差分数组。
结论：s[n]是原数组a[n]的前缀和数组、a[n]是原数组s[n]的差分数组。
差分数组的用处
差分数组和前缀和数组的用途相似，都是面对以区间为单位进行操作的需求。
差分将对区间进行的增减操作由O(n)优化为O(1)。
以下给出一道题目：
题目描述：
输入一个长度为 n的整数序列。接下来输入 m个操作，每个操作包含三个整数 l,r,c，表示将序列中 [l,r]之间的每个数加上 c。
请你输出进行完所有操作后的序列。
我们需要对一个区间进行加减操作，如果按照朴素思想，我们需要从左端点遍历都右端点，时间复杂度为O(n)。进行m次操作的时间复杂度就是O(mn)。
而对差分数组进行操作，再求一遍前缀和的时间复杂度是O(m+n)
如图，对查分数组的某一个元素+1，则原数组从这个元素开始的元素都会加一。
因此，再让区间外的第一个元素减一就能实现这个区间内的元素加一，以此类推。
{
#include <iostream>
#define N 100010
using namespace std;
int f[N];
int s[N];
int main()
{
int n,m;
cin >> n >> m;
for(int i = 1; i <= n; i++)
{
cin >> f[i];
s[i] = f[i] - f[i-1];
}
while(m--)
{
int l,r,c;
cin >> l >> r >> c;
s[l] += c;
s[r+1] -= c;
}
for(int i =1 ; i <= n; i++)
{
f[i] = f[i-1] + s[i];
cout << f[i] << ' ';
}
}
}
二维差分
同样地，二维数组也有差分。其目的仍然是对区间(子矩阵)进行操作。
在一维数组中，我们改变原数组的某一元素，会改变前缀和数组一段区间的值。
同样，在二维数组中，我们改变原数组的某一元素，会改变前缀和数组一个子矩阵的值。
首先，二维数组前缀和的几何意义是，从矩阵左上角到该元素的元素和。
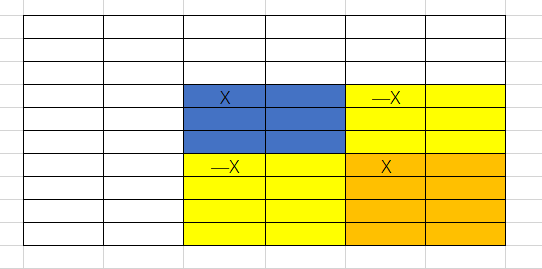
如图中的前缀和数组的(i,j)元素表示的是原数组绿色部分的元素和。
那么我们给这个原数组中元素加上一个1，前缀和数组在下图中的黄色部分都会加上一个1（该元素到矩阵右下角）。
现在我们要让蓝色部分加上一个值X，但显然这样操作仍会对黄色部分加上值X。那么我们再让黄色区域减去这个X即可，同一维的是一个道理，注意重复的地方要加上一个X。
class Solution {
public:
vector<vector<int>> rangeAddQueries(int n, vector<vector<int>>& queries) {
vector<vector<int>> tmp(n+1 , vector<int>(n+1,0));
int m = queries.size();
for(int i = 0; i < m; i++)
{
tmp[queries[i][0]][queries[i][1]]++;
tmp[queries[i][0]][queries[i][3]+1]--;
tmp[queries[i][2]+1][queries[i][1]]--;
tmp[queries[i][2]+1][queries[i][3]+1]++;
}//对差分数组进行操作
vector<vector<int>> ans(n , vector<int>(n , 0));
ans[0][0] = tmp[0][0];
for(int i = 0; i < n; ++i)
for(int j = 1; j < n; ++j) tmp[i][j] += tmp[i][j-1];
for(int i = 1; i < n; ++i)
for(int j = 0; j < n; ++j) tmp[i][j] += tmp[i-1][j];
for(int i = 0; i < n; ++i)
for(int j = 0; j < n; ++j) ans[i][j] = tmp[i][j];
//由于下标从0开始，所以分布求前缀和要方便一点
//这种写法不存在重复加的地方，第一个for求一维前缀和，第二个for加上前面行的和。
return ans;
}
};
