【数组】 前缀和补充

【数组】 前缀和补充

考虑到昨天写的前缀和博客有所欠缺，所以写这篇博客作为上一篇博客的补充。

二维数组的前缀和

首先，我们从先前提到过的一维数组的前缀和谈起。

而一维数组的前缀“和”的作用便是对以区间为单位进行操作，
我们基于这个概念，引入二维数组的前缀和。

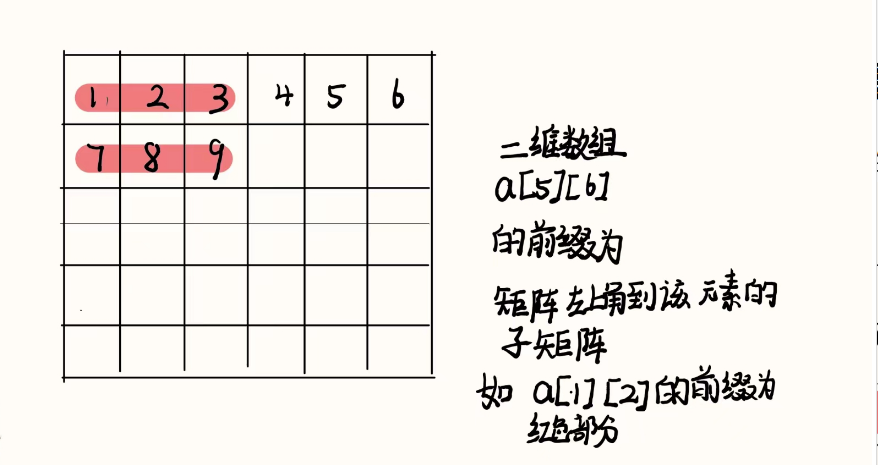
那么二维数组的前缀和，也就是矩阵中一个子矩阵的元素和。
其中右下角a[4][5]的前缀和就是矩阵所有元素的和。
同样的，二维数组的前缀“和”对以二维区间，也就是子矩阵为单位进行操作。

求二维数组的前缀和也很简单，只需要明确概念后画图进行模拟即可。
假设，我们有要对二维数组中的某一个元素求前缀和，类比一维数组的递推表达式s[n] = s[n-1] + a[n]，我们同样可以写出一个递推表达式。

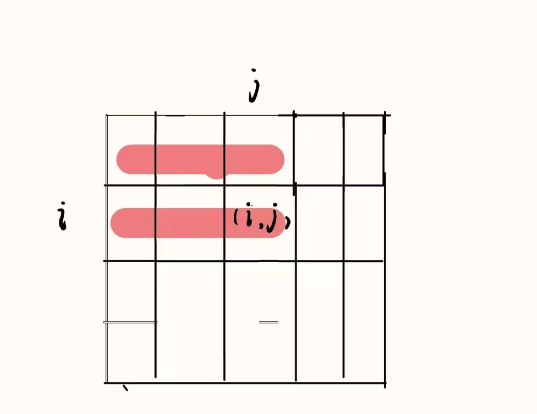
如图，我们要求红色区域，即元素(i,j)的前缀和，类比一维求法，我们同样根据先前求出来的前缀和加上(i,j)元素求前缀和。

则 为绿色部分 + 蓝色部分 - 混色部分 + (i,j)值
假设前缀和数组为s[i][j] , 原数组为a[i][j];

我们得到关系式：s[i][j] = s[i-1][j](蓝色) + s[i][j-1](绿色) -s[i-1][j-1](混色) + a[i][j]；

借助几何意义，我们同样可以推出子矩阵的和的公式。

给出四个整数 x1,y1,x2,y2，表示一个子矩阵的左上角坐标和右下角坐标

s[x2][y2] - s[x2][y1-1]-s[x1-1][y2] + s[x1-1][y1-1]

以下给出一道例题作为参考。

题目出自acwing，侵删。
以下为代码

{
    #include <iostream>
    #define N 1010
    using namespace std;
    int f[N][N];
    int s[N][N];
    int main()
    {
        int n,m,q;
        cin >> n >> m >> q;
        for(int i = 1; i <= n; i++)
            for(int j = 1; j <= m; j++){
                cin >> f[i][j];
                s[i][j] = s[i][j - 1] + s[i - 1][j] - s[i - 1][j - 1] + f[i][j];
            }
        while(q--)
        {
            int x1,y1,x2,y2;
            cin >> x1 >> y1 >> x2 >> y2;
            cout << s[x2][y2] - s[x2][y1-1]-s[x1-1][y2] + s[x1-1][y1-1] << endl;//通过对前缀和进行运算求子矩阵的和；
        }
        return 0;
    }
}