【数组】前缀和
前缀和
给出一个数列:
1 2 3 4 5 6 7 8 9
它的前缀和:
1 3 6 10 15 21 28 36 45
前缀和即:从第一个元素到该元素之和
通常我们会在数组中触及到这类知识。
假设给出原数组 a[5] = {1,2,3,4,5},我们可以得到前缀和数组,假设为S[5] = {1,3,6,10,15}。
那么可以得到: S[n] = S[n-1] + a[n],即求前缀和的公式。
那么前缀和数组有什么用呢?
以下给出一道经典前缀和问题:
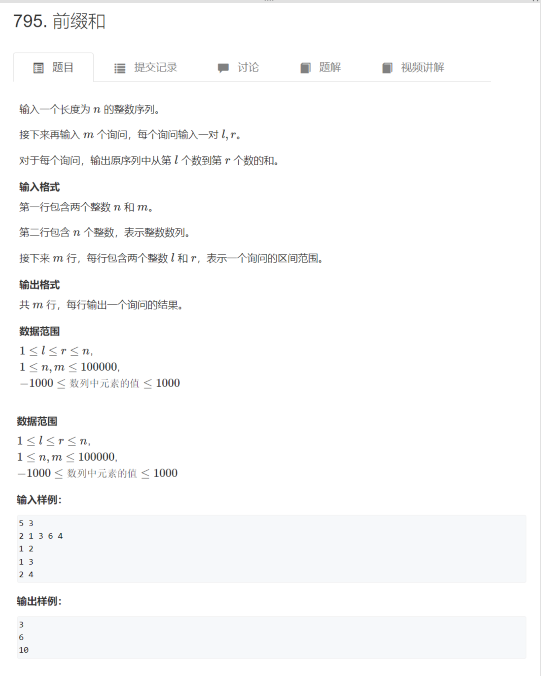
(题目出自acwing,侵删)
首先我们先从朴素思想开始考虑,求m次区间和的时间复杂度是O(mn2)
while(m--)
{
int l , r;
cin >> l >> r;
int sum = 0;
for(int i = l; i <= r; i++)
{
sum += num[i];(假设下标从1开始)
}
cout << sum << endl;
}
我们会发现,我们没求一次区间和,就要循环一次,那么有没有一种方法可以让O(n)的求和变为O(1)的时间复杂度呢?
答案就是使用前缀和。对区间[l,r],通过对求前缀和过程的分析可以的出,区间和为s[r]-s[l-1]。因此我们可以通过一次运算求出原数组任意一段数据的和。
以下为代码:
点击查看代码
#include<iostream>
#define N 100010
using namespace std;
int nums[N];
int s[N];
int main()
{
int n,m;
cin >> n >> m;
for(int i = 0; i < n; i++)
{
cin >> nums[i+1];
s[i+1] = s[i] + nums[i+1];//求前缀和
}
while(m--)
{
int l,r;
cin >> l >> r;
cout << s[r]-s[l-1] << endl;//
}
return 0;
}
题目
前缀和结合哈希表
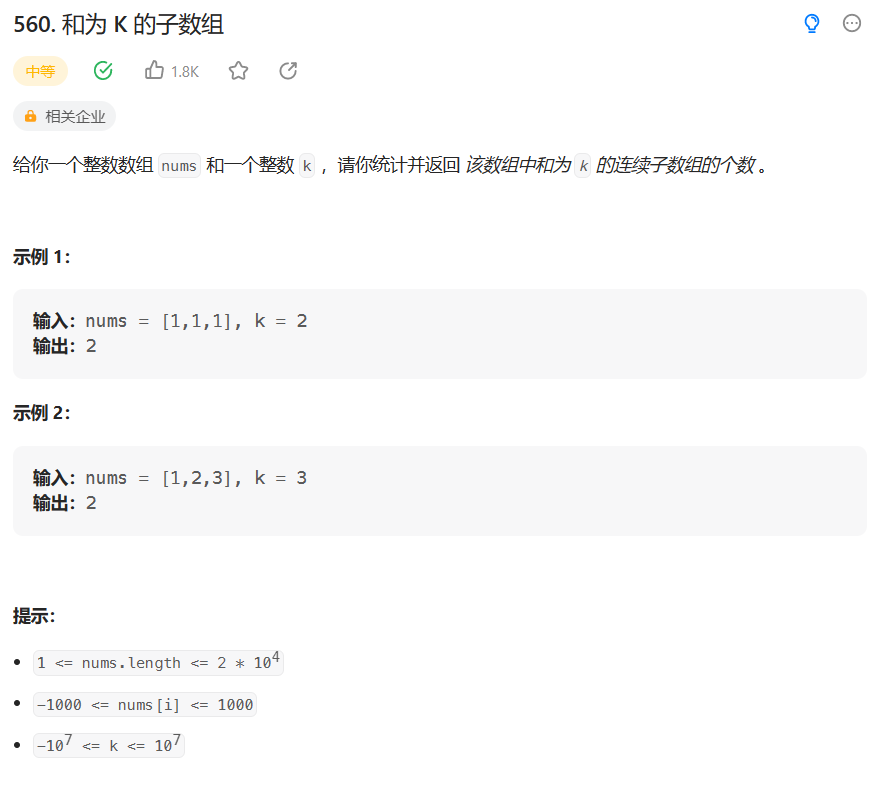
https://leetcode.cn/problems/subarray-sum-equals-k/
在数组中:
1.子数组
子数组的定义:一个或连续多个数组中的元素组成一个子数组(子数组最少包含一个元素)
2.子序列
子序列的定义:子序列就是在原来序列中找出一部分组成的序列(子序列不一定连续)
如果使用for嵌套循环暴力枚举O(n2)的方法必然会超时。
那么分析题意,可知求区间和为k的区间个数,即 s[i] - s[j] == k
同样,如果对前缀和数组进行枚举同样是O(n2)的时间复杂度,会超时。
我们用哈希表存储前缀和数组,结合公式s[i] - s[j] == k的变形s[j] = s[i] - k就可以实现O(n)的时间复杂度的解法。
即:对每一个前缀和数组元素s[i],利用哈希表查找s[i] - k是否存在,存在则找到了一个或n个符合题意的区间。
以下为代码
点击查看代码
class Solution {
public:
int subarraySum(vector<int>& nums, int k) {
unordered_map<int, int> mp;
mp[0] = 1;
int sum = 0;
int ans = 0;
for(int i = 0; i < nums.size(); i++)
{
sum += nums[i];
if(mp.find(sum - k) != mp.end())//
ans += mp[sum - k];
mp[sum]++;
}
return ans;
}
};
前缀乘积


https://leetcode.cn/problems/subarray-sum-equals-k/
最先想到的是遍历求乘积,也就是O(n2)的暴力算法,但这不符合题目的要求。
那么我们需要对算法进行优化,从朴素思想出发,遍历求乘积时,从0到n-1累乘,中间跳过i,那么天然地由i分为左右两个区间,根据乘法的结合律,得出answer[i] = i左侧元素的乘积*i右侧元素的乘积。
那么我们只需要提前将每一个i左侧、右侧元素的乘积算出来,就可以实现O(n)时间复杂度的算法。
点击查看代码
class Solution {
public:
vector<int> productExceptSelf(vector<int>& nums) {
int n = nums.size();
vector<int> answer(n);
vector<int> l(n);
vector<int> r(n);
l[0] = 1;
r[n - 1] = 1;
for(int i = 1; i < n; i++)
l[i] = l[i-1]*nums[i-1];
for(int i = n - 2; i >= 0; i--)
r[i] = r[i+1]*nums[i+1];
for(int i = 0; i < n; i++)
answer[i] = l[i]*r[i];
return answer;
}
};

