Fibnacci数列

Fibnacci数列

Fibnacci数列定义

• 斐波那契数列（Fibonacci sequence），又称黄金分割数列，因数学家莱昂纳多·斐波那契（Leonardo Fibonacci）以兔子繁殖为例子而引入，故又称为“兔子数列”，指的是这样一个数列：1、1、2、3、5、8、13、21、34、……在数学上，斐波那契数列以如下被以递推的方法定义：F(0)=0，F(1)=1, F(n)=F(n - 1)+F(n - 2)（n ≥ 2，n ∈ N*）在现代物理、准晶体结构、化学等领域，斐波那契数列都有直接的应用，为此，美国数学会从 1963 年起出版了以《斐波那契数列季刊》为名的一份数学杂志，用于专门刊载这方面的研究成果。
  (百度百科 )

• 这个数列从第3项开始，每一项都等于前两项之和。

• 斐波那契数列的定义者，是意大利数学家莱昂纳多·斐波那契（Leonardo Fibonacci），生于公元1170年，卒于1250年，籍贯是比萨。他被人称作“比萨的莱昂纳多”。1202年，他撰写了《算盘全书》（Liber Abacci）一书。他是第一个研究了印度和阿拉伯数学理论的欧洲人。他的父亲被比萨的一家商业团体聘任为外交领事，派驻地点于阿尔及利亚地区，莱昂纳多因此得以在一个阿拉伯老师的指导下研究数学。他还曾在埃及、叙利亚、希腊、西西里和普罗旺斯等地研究数学。另外斐波那契还在计算机C语言程序题中应用广泛。

Fibnacci数列的递归表达式

F(0)=0，F(1)=1, F(n)=F(n - 1)+F(n - 2)（n ≥ 2，n ∈ N*）

C语言实现

递归算法
#include <stdio.h>
int Fib(int n)
{
    if (n == 0)
        return 0;
    if (n == 1)
        return 1;
    if (n > 1)
        return (Fib(n - 1) + Fib(n - 2));
}
    int main()
{
    int n = 0;
    scanf("%d", &n);
    printf("%d\n", Fib(n));
    return 0;
} 

上网查询后得知递推算法的时间复杂度是O(2^n)，n的值一大就需要花费大量时间，使用递归算法我的电脑计算到40就会卡住

递推算法
#include <stdio.h>
int Fib(int n)
{
    int i = 0;
    int x = 0;
    int y = 1;
    int z = 0;
    if (n == 0)
    {
        return 0;
    }
    if (n == 1)
    {
        return 1;
    }
    if (n > 1)
    {
        for (i = 0; i < n - 1; i++)
        {
            z = x + y;
            x = y;
            y = z;
        }
        return z;
    }
}
int main()
{
    int n = 0;
    scanf("%d", &n);
    printf("%d\n", Fib(n));
    return 0;
}  

递推的算法比递归的算法效率更高，时间复杂度是O(n);
如果想要进一步提高效率，可以保存每一步算的F（n）用作下一步计算。
当n=47时，数据已经开始溢出了。

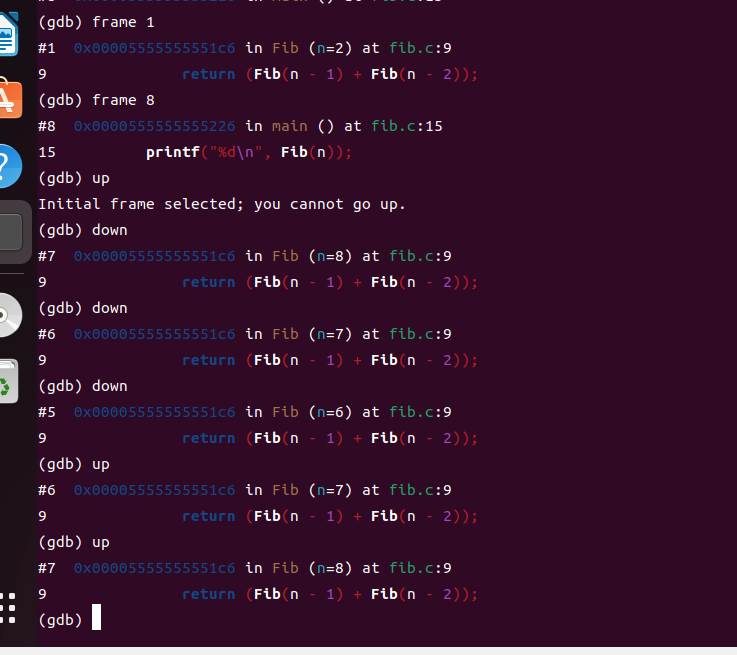
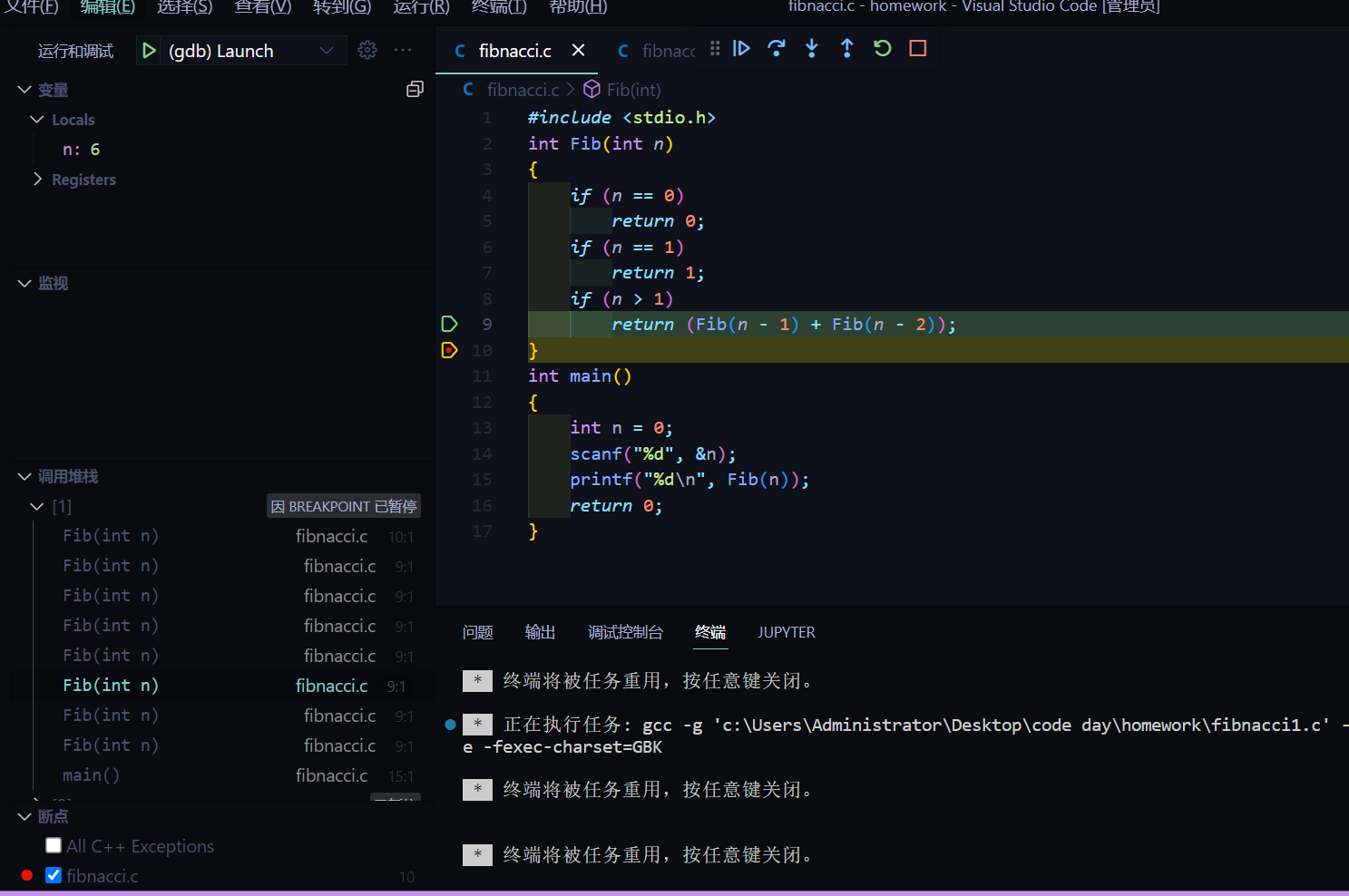
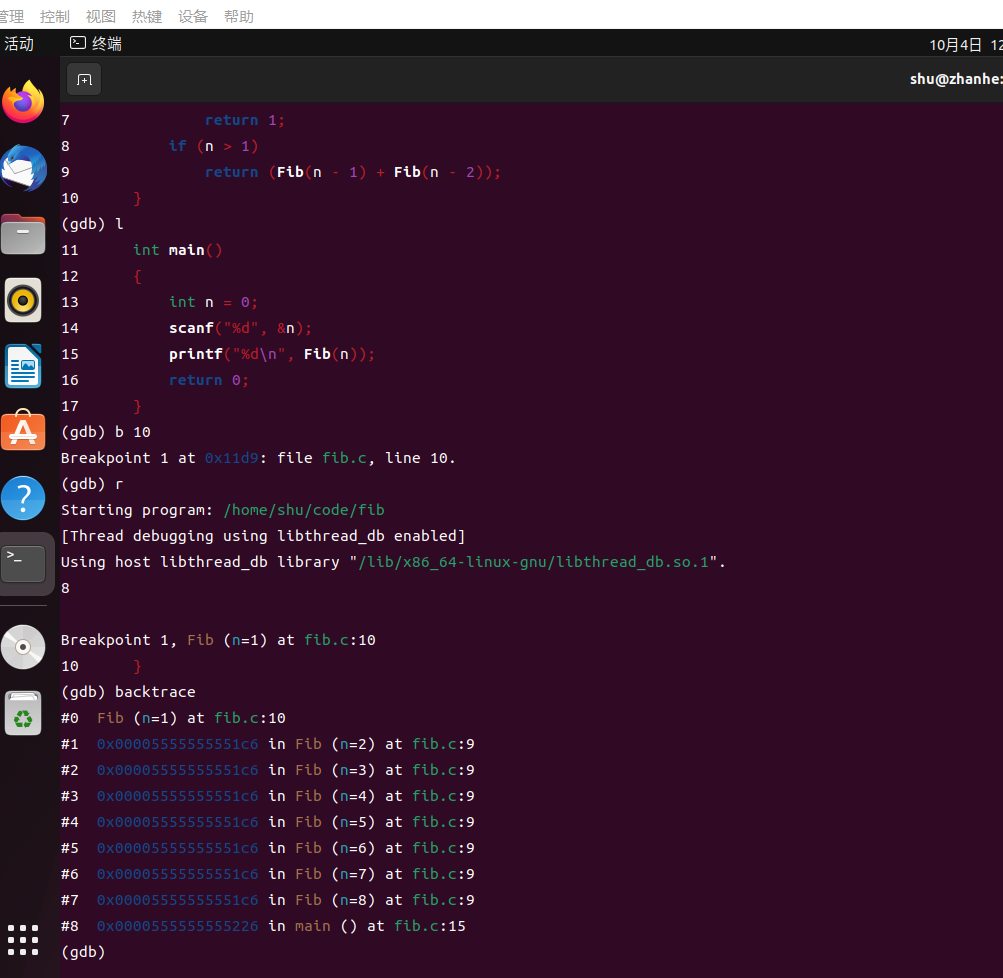
调试查看堆栈情况