最小树形图及其生产方法

诸位看官，这是我第一次在整篇文章的所有图片里面加水印。小弟写博客的时间不长，就有两篇博客被盗用并未注明原文网址。这一方面使我痛心不已，另一方面迫使我不得不重新考虑一下版权保护问题。小弟不是吝啬鬼，如果影响阅读或者是确实需要我的图片的，请私信我，我将免费为有需求的看官提供图片。谢谢了！

---

 

最小树形图（Arborescence，亦称Directed Rooted Tree）是有向图的最小生成树（Minimum Spanning Tree）。本博客旨在详细的介绍最小树形图的生成方法，但不涉及具体的数学推导。先看一副有向权重图：

我们该如何求这幅图的一个最小树形图呢？我们在这里给出求最小树形图的一个流程图，该流程图是经典的Zhu-Liu算法：

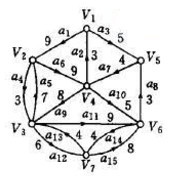
上图中已经详细的给出了最小树形图的全部步骤，现在给出如何解决Step2中更新“以前指向该环中的任意节点的路径”的办法。假定环路中存在一点v，环中有一条边e1指向该点。环外有一条边e2指向该点。则e2更新后，新边的权重e2_new=e2_old-e1（环外边权重减环内边权重）。

下面是针对本文开始所给出的图生成最小树形图的完整步骤：

算法开始（原图）：

 

现在指定根节点为V1，即生成根节点为V1的最小树形图。（也可指定其他节点，这里以V1为例）

根据流程图中Step1的规则，根节点V1不用选择指向该点的最小权重边；指向V2的最小权重边为a5；指向V3的最小权重边为a4；指向V4的最小权重边为a7；指向V5的最小权重边为a8；指向V6的最小权重边为a10；指向V7的最小权重边为a14；如下图：

上图中有两个环，分别为由V2-V3组成的环和由V4-V5-V6组成的环。现在根据Step2分别对两个环路进行治理。

首先治理V2-V3环：

第一步：缩环为点，如下图左侧的大圆点（缩环为点后a4,a5边被取消，其余所有边保留）

第二步：对于所有从大圆点出去的边，其权重保持不变；对于所有指向大圆点的边，更新其权值。在这里采用W[e]表示边e的权重；用W[e]_New表示边e更新后的权重；W[e]_Old表示边e更新前的权重。

W[a1]_New = W[a1]_Old - W[a5] =9-7=2

W[a9]_New = W[a9]_Old - W[a4] =8-3=5

W[a13]_New = W[a13]_Old - W[a4] =4-3=1

边缘权重更新后的图如下图所示：

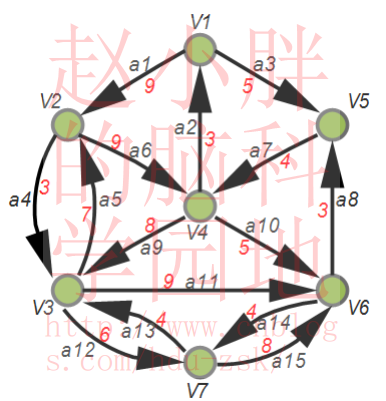
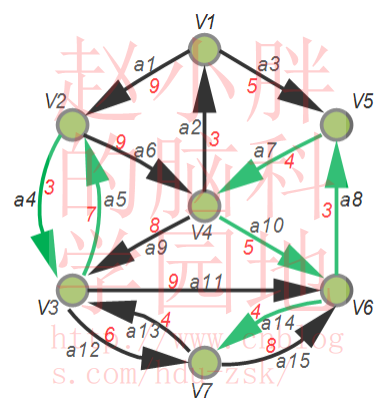
其次治理V4-V5-V6环：
第一步：缩环为点，如下图右侧的大圆点（缩环为点后a7,a8,a10边被取消，其余所有边保留）
第二步：对于所有从大圆点出去的边，其权重保持不变；对于所有指向大圆点的边，更新其权值。
W[a3]_New = W[a3]_Old - W[a8] =5-3=2
W[a6]_New = W[a6]_Old - W[a7] =9-4=5
W[a11]_New = W[a11]_Old - W[a10] =9-5=4
W[a15]_New = W[a15]_Old - W[a10] =8-5=3
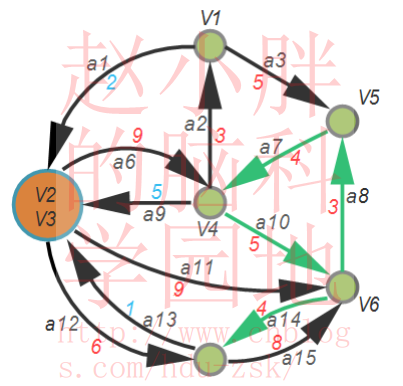
边缘权重更新后的图如下图所示：

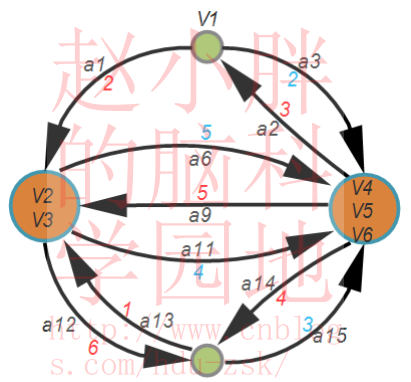
对于新到的图，按照Step1中的描述，重新寻找除V1以外，指向其他节点的最小边。其结果如下图所示：

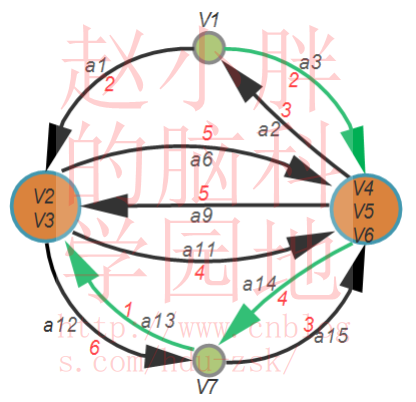
指向V2V3节点的最小边为a13，指向V7节点的最小边为a14；指向V4V5V6节点的最小边为a3。原论文中证明，a3,a14,a13一定是以V1为根的最小树形图的边集的子集，现在对V2V3节点和V4V5V6节点做展开操作。我们回到原图中（权重全部恢复到原图的权重），并标记a3,a14,a13这三条边，如下图：

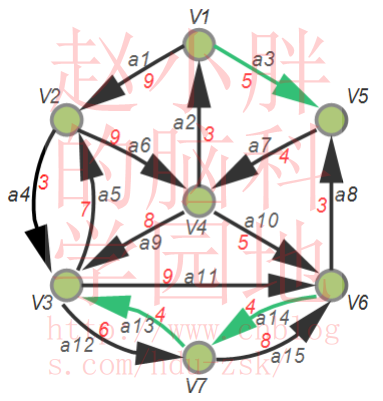
不难发现如果从根节点V1发出的信息想要顺畅的流到V4，则只能选择a7；同理，如果从V1出发的信息流想要顺畅的流到V6，则只能选择经V4到V6的a10。因此，a7,a10在边集内。同理如果从V1发出的信息想要流向V2，则只能选择经V3到V2方向的a5。此时所有的节点都有边相连。新从根节点V1，可以顺有向边的方向到任意节点，如下图：

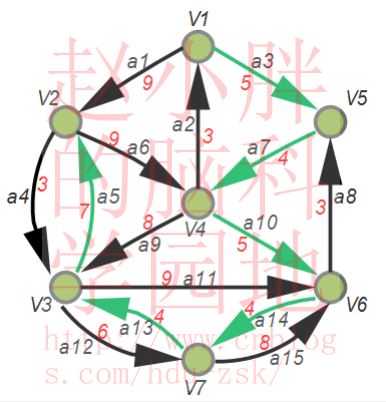
上图即是以 V1 为根节点的最小树形图。