树和图详解

（1）二叉树的性质

　　1、在二叉树的第 i 层上至多有2^(i-1)个节点

　　2、深度为 k 的二叉树至多有2^(k)-1个节点

　　3、对于任何一个二叉树，若其叶子节点数为n1，度为2的节点数为n2，则n1=n2+1

　　　　树的节点树=所有节点度之和+1

　　4、具有n个节点的完全二叉树的深度为floor(log(2,n))+1

（2）图基本概念

　　1、图：一种表示“多对多”关系的复杂数据结构。

　　2、图的组成：图G由一个非空的有限顶点集合V(G)和一个有限边集合E(G)组成，定义为G=(V，E)。

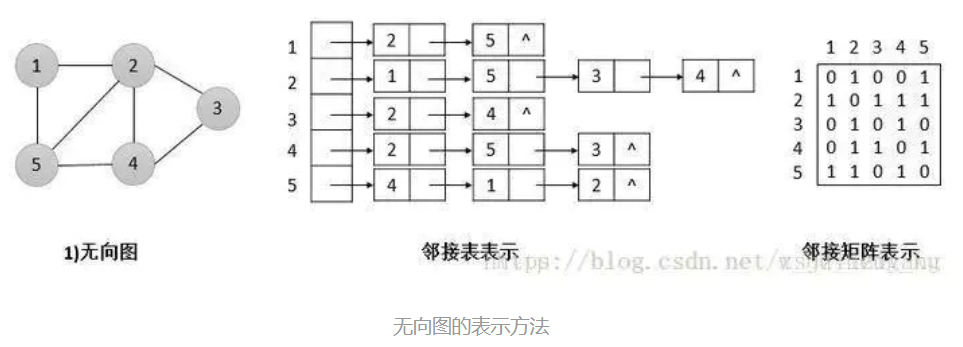
　　3、无向图：若图的每条边都没有方向，则称该图为无向图。

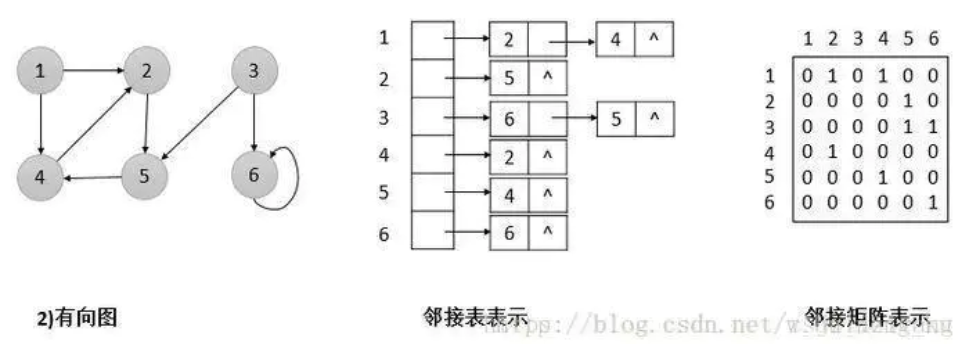
　　4、有向图：若图的每条边都有方向，则称该图为有向图。

　　5、对于无向图，顶点的度表示以该顶点作为一个端点的边的数目。

　　6、对于有向图，顶点的度分为入度和出度。入度是以该顶点为终点的入边数目，出度是以该顶点为起点的出边数目，该顶点的度等于其入度和出度之和。

　　7、路径：在图G中，存在一个顶点序列(Vp,Vi1,Vi2,Vi3…,Vin,Vq)，使得(Vp,Vi1)，(Vi1,Vi2)，…,(Vim,Vq)均属于边集E(G)，则称顶点Vp到Vq存在一条路径。

　　8、路径长度：一条路径上经过的边的数量。

　　9、环：某条路径包含相同的顶点两次或两次以上。

　　10、有向无环图：没有环的有向图，简称DAG。

　　11、带权有向图的最短路径长度：源点Vm到终点Vn的所有路径中，权值和最小的路径是最短路径，其长度是最短路径长度。

　　12、完全图：任意两个顶点都相连的图称为完全图，又分为无向完全图和有向完全图。　　

　　13、连通图：在无向图中，若任意两个顶点vivi与vjvj都有路径相通，则称该无向图为连通图。

　　14、强连通图：在有向图中，若任意两个顶点vivi与vjvj都有路径相通，则称该有向图为强连通图。

　　15、连通网：带权值的连通图叫做连通网。

　　16、生成树：将图中所有顶点以最少的边连通的子图。生成树包含全部n个顶点，有且仅有n-1条边，在添加边则必定成环。（因为每个结点（除根结点）都可以向上找到唯一的父节点，所有是树）。

　　17、最小生成树：在所有生成树中，权值和最小的生成树就是最小生成树。

　　18、树与图的关系：树的定义：有且只有一个结点的入度为0，其他节点的入度为1。树是一个无向连通图，其中任何两个顶点只通过一条路径连接。 换句话说，一个任何没有简单环路的连通图都是一棵树。

（2）图的表示

　　1、邻接矩阵：使用一个二维数组 G[N][N]存储图，如果顶点 Vi 和 顶点 Vj 之间有边，则 G[Vi][Vj] = 1 或 weight。邻接矩阵是对称的。

　　2、邻接表：图的一种链式存储结构：对于图 G 中每个顶点 Vi，把所有邻接于 Vi 的顶点 Vj 链成一个单链表，这个单链表称为顶点 Vi 的邻接表。

　　邻接表与邻接矩阵的区别：邻接表占用空间少，适合存储稀疏图；邻接矩阵适合存储稠密图。若判断任意两个结点之间是否有边连接，可用邻接矩阵。

    

 

（3）图的遍历

　　1、基于邻接矩阵

public class Graph {
    //顶点数量
    private int vertexSize;
    //顶点数组
    private int[] vertexs;
    private int[][] matrix;
    //设置不可到达的权值为1000
    private static final int max=1000;
    private boolean[] isVisited;
    
    public Graph(int vertexSize){
        this.vertexSize=vertexSize;
        matrix=new int[vertexSize][vertexSize];
        vertexs=new int[vertexSize];
        for(int i=0;i<vertexSize;i++){
            vertexs[i]=i;
        }
        isVisited=new boolean[vertexSize];
    }
    public int[] getVertexs() {
        return vertexs;
    }
 
    public void setVertexs(int[] vertexs) {
        this.vertexs = vertexs;
    }
    //获取某个顶点的出度
    public int getOutDegree(int index){
        int degree=0;
        for(int j=0;j<matrix[index].length;j++){
            int weight=matrix[index][j];
            if(weight!=0&&weight!=MAX_WEIGHT){
                degree++;
            }
        }
        return degree;
    }
    
    //获取两个顶点之间的权值
    public int getWeight(int v1,int v2){
        return matrix[v1][v2]==0?0:(matrix[v1][v2]==MAX_WEIGHT?-1:matrix[v1][v2]);
    }
    
    // 获取某个顶点的第一个邻接点
    public int getFirstNeigbour(int index){
        for(int j=0;j<vertexSize;j++){
            if(matrix[index][j]>0&&matrix[index][j]<MAX_WEIGHT){
                return j;
            }
        }
        return -1;
    }
    
    // 图的深度优先遍历算法
    private void depthFirstSearch(int i){
        isVisited[i]=true;
        int w=getFirstNeigbour(i);
        while(w!=-1){
            if(!isVisited[w]){
                //需要遍历该顶点
                System.out.println("访问到了："+w+"顶点");
                depthFirstSearch(w);
            }
            w=getNextNeighbour(i, w);
        }
    }
    
    public void depthFirstSearch(){
        isVisited=new boolean[vertexSize];
        for(int i=0;i<vertexSize;i++){
            if(!isVisited[i]){
                System.out.println("访问到了："+i+"顶点");
                depthFirstSearch(i);
            }
        }
        isVisited=new boolean[vertexSize];
    }
    
    public static void main(String[] args) {
        Graph graph=new Graph(9);
        int[] a1=new int[]{0,10,max,max,max,11,max,max,max};
        int[] a2=new int[]{10,0,18,max,max,max,16,max,12};
        int[] a3=new int[]{max,max,0,22,max,max,max,max,8};
        int[] a4=new int[]{max,max,22,0,20,max,max,16,21};
        int[] a5=new int[]{max,max,max,20,0,26,max,7,max};
        int[] a6=new int[]{11,max,max,max,26,0,176,max,max};
        int[] a7=new int[]{max,16,max,max,max,17,0,19,max};
        int[] a8=new int[]{max,max,max,16,7,max,19,0,max};
        int[] a9=new int[]{max,12,8,21,max,max,max,max,0};
        graph.matrix[0]=a1;
        graph.matrix[1]=a2;
        graph.matrix[2]=a3;
        graph.matrix[3]=a4;
        graph.matrix[4]=a5;
        graph.matrix[5]=a6;
        graph.matrix[6]=a7;
        graph.matrix[7]=a8;
        graph.matrix[8]=a9;
        int degree=graph.getOutDegree(1);
        System.out.println("出度："+degree);
        int weight=graph.getWeight(0, 4);
        System.out.println("权值："+weight);    
        graph.depthFirstSearch();
    }
}

　　2、基于邻接表

　　1）图的数据结构

package graph;

import java.util.*;

public class graphNode {
    public int val;
    public List<graphNode> neighbors;
    public boolean visited;

    public graphNode() {
        val = 0;
        neighbors = new ArrayList<graphNode>();
    }

    public graphNode(int _val) {
        val = _val;
        neighbors = new ArrayList<graphNode>();
    }

    public graphNode(int _val, ArrayList<graphNode> _neighbors) {
        val = _val;
        neighbors = _neighbors;
    }
}

　　2）图的深度优先遍历和广度优先遍历

package graph;
import java.util.*;
public class create_And_Visited_Graph {
    //邻接表如下
    /*
    1->2-5
    2->1-5-4
    3->2-4
    4->2-5-3
    5->4-1-2
     */
    public static void main(String[] args) {
        //创建图节点
        graphNode n1=new graphNode(1);
        graphNode n2=new graphNode(2);
        graphNode n3=new graphNode(3);
        graphNode n4=new graphNode(4);
        graphNode n5=new graphNode(5);

        //创建邻接表
        n1.neighbors.add(n2);
        n1.neighbors.add(n5);

        n2.neighbors.add(n1);
        n2.neighbors.add(n5);
        n2.neighbors.add(n4);

        n3.neighbors.add(n2);
        n3.neighbors.add(n4);

        n4.neighbors.add(n2);
        n4.neighbors.add(n5);
        n4.neighbors.add(n3);

        n5.neighbors.add(n4);
        n5.neighbors.add(n1);
        n5.neighbors.add(n2);
        //深度优先遍历
        DFS(n1);
//        System.out.println();
        //广度优先遍历
//        BFS(n1);

    }
    //深度优先遍历
    public static void DFS(graphNode root){
        if (root == null) {
            return;
        }
        root.visited=true;
        System.out.print(root.val+" ");
        for (graphNode node : root.neighbors) {
            if (!node.visited) {
                DFS(node);
            }
        }
    }

    //广度优先遍历
    public static void BFS(graphNode root) {
        Queue<graphNode> queue = new LinkedList<>();
        queue.offer(root);
        root.visited=true;
        while (!queue.isEmpty()) {
            graphNode r = queue.poll();
            System.out.print(r.val+" ");
            for (graphNode node : r.neighbors) {
                if (!node.visited) {
                    queue.offer(node);
                    node.visited=true;
                }
            }
        }
    }
}