算法Top的几种解法
一、全局排序
任何排序算法均可,但是时间复杂度或者空间复杂度不符合要求。明明只需要TopK,却将全局都排序了,这也是这个方法复杂度非常高的原因。那能不能不全局排序,而只局部排序呢?这就引出了第二个优化方法局部排序。
二、局部排序
(1)冒泡排序:每冒一个泡,找出最大值,冒k个泡,就得到TopK
伪代码:
for(i=1 to k){
bubble_find_max(arr,i);
}
冒泡排序,将全局排序优化为了局部排序,非TopK的元素是不需要排序的,节省了计算资源,时间复杂度O(n*k)。不少朋友会想到,需求是TopK,是不是这最大的k个元素也不需要排序呢?这就引出了第三个优化方法堆排序。
三、堆排序
思路:只找到TopK,不排序TopK。
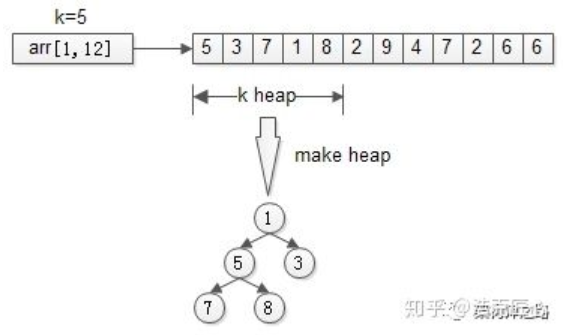
步骤一:先用前k个元素生成一个小顶堆,这个小顶堆用于存储,当前最大的k个元素。
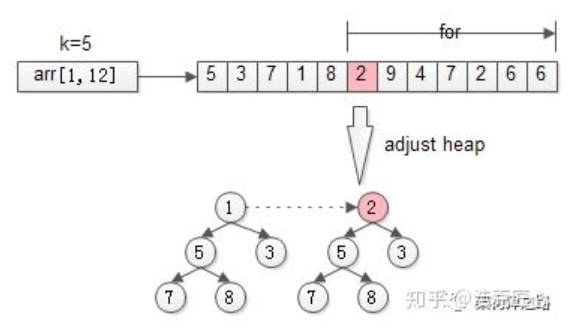
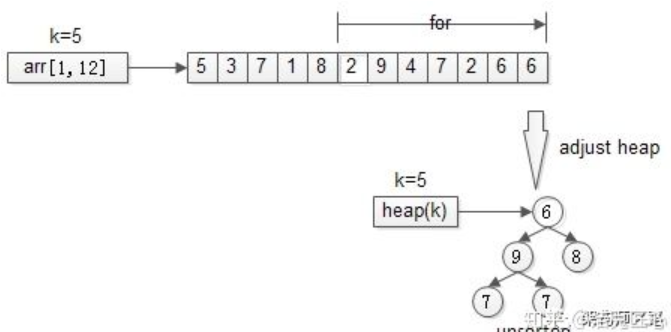
步骤二:从第k+1个元素开始扫描,和堆顶(堆中最小的元素)比较,如果被扫描的元素大于堆顶,则替换堆顶的元素,并调整堆,以保证堆内的k个元素,总是当前最大的k个元素。
步骤三:扫描完所有n-k个元素,最终堆中的k个元素,即得TopK。
时间复杂度:O(n*lg(k))
伪代码:
heap[k] = make_heap(arr[1, k]);
for(i=k+1 to n){
adjust_heap(heep[k],arr[i]);
}
return heap[k];
 =>
=> =>
=> 


 浙公网安备 33010602011771号
浙公网安备 33010602011771号