BUAA_OO_第三单元总结
摘要
本单元的主要任务是根据JML规格来撰写代码,JML作为一种行为接口规格语言,可以帮助开展规格化设计,JML本身的描述是逻辑严格的,所以程序员再根据JML规格编写代码时不会发现二义性。除此之外,由于本单元的主要目的是模拟一个社交网络,其中需要我们实现图的相关算法,而且对我们编写的方法的复杂度有一定的限制。因此,本单元的主要难点包括:
-
阅读JML规格,正确理解其含义并实现相关接口。
-
应用图有关的算法(判断两节点是否可达,最小生成树,最短路径)
-
保证实现的所有方法的时间复杂度可以满足限制(实际上,保证每个方法的时间复杂度小于O(n^2)即可)
第9次作业
架构设计
整体的架构其实官方代码已经给出了,我们的主要任务是根据JML规格去实现相关接口,本次作业的主要难点是对isCircle方法的实现,isCircle的目的是判断整个图中的两个人是否存在一条路径相连,即可达。对于DFS和BFS算法,如果采用二维矩阵来存储图的信息的话,其时间复杂度可以达到O(n^2),如果采用邻接表来存储图时,时间复杂度可以达到O(n+e),所以如果图比较稠密复杂的话,目测效果不是很好。因此,可以采用并查集的算法来进行优化,并查集的特点就是忽略了图的具体形状,可以用于处理一些不相交集合的合并和查询问题,利用并查集可以将该方法优化到近似于O(1),效果甚佳。参考代码在
在编写代码的过程中,我并没有将并查集当作成一个普通的算法,而是将其单独写成了一个类,按照正常思维,算法或许无法当成对象来看待,但是我们可以将算法当成一种操作黑箱,在一些情况下我们需要维护这个黑箱,在我们需要某些结果时利用黑箱来获得,这种算法的解耦也对我的下一次作业提供了便利。
Uml类图如下:
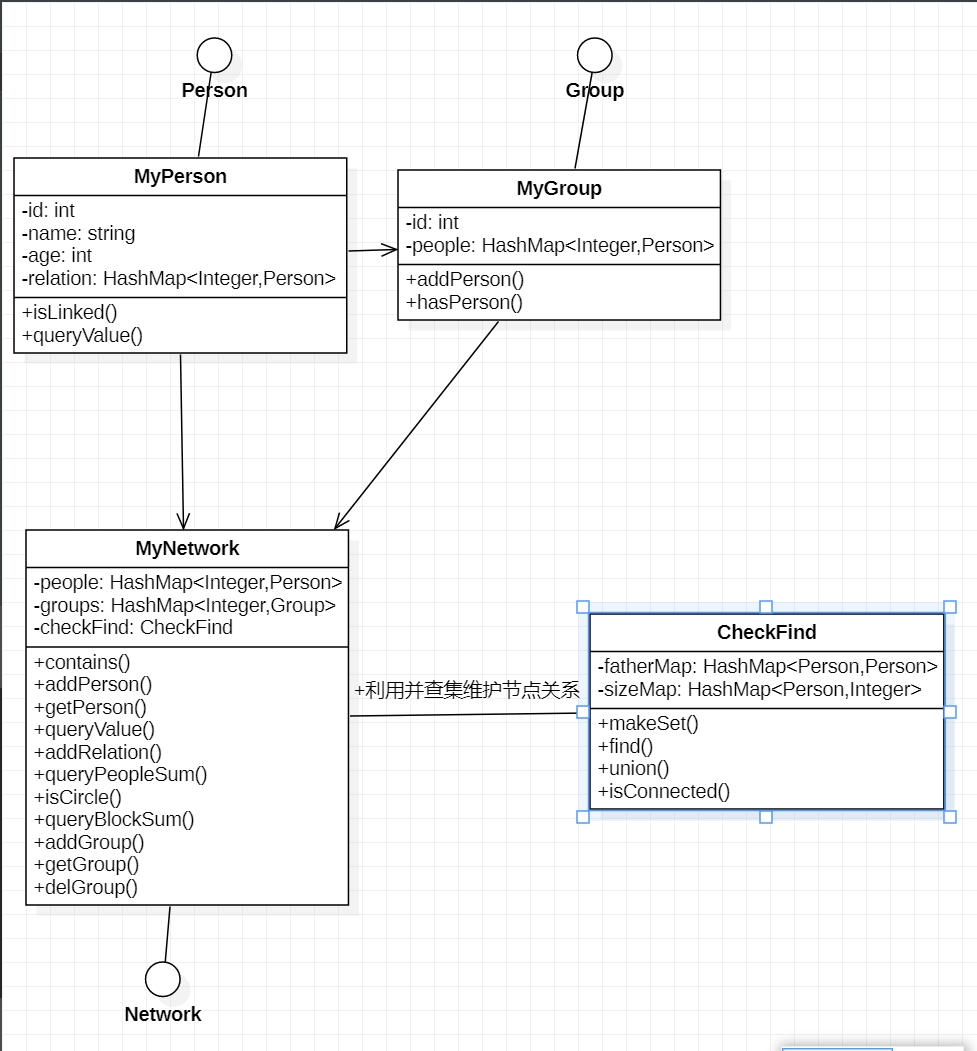
优化和维护策略
本次作业除了isCircle外需要考虑优化维护的代码并不多,不过有一点可以注意一下,就是Network里的Person和Group的数组可以采用HashMap来存储,可以利用其id作为key,这样在查询Person和Group的时候复杂度可以达到O(1),而采用ArrayList的复杂度会高一些,当然使用ArrayList似乎不会在强测中超时,但是HashMap更加方便一些。
第10次作业
架构设计
和上一次相比这次作业需要实现的方法增加了不少,其中难度比较高的方法就是sendMessage和queryLeastConnection,前者倒没有涉及到复杂的算法,其难点主要在于JML的阅读。而后者在JML的阅读和实现上都是本次作业需要特别注意的,其JML规格非常复杂,括号嵌套也很多,需要对其进行拆分来理解,下面先来稍微介绍一些queryLeastConnection的JML分析过程。
1.\min Person[] subgroup 说明对于一个Person数组subgroup需要满足某些条件
2.需要满足的条件,根据&&进行拆分,拆成了4个条件,意味着subgroup需要同时满足这4个条件:
(1)subgroup.length % 2 == 0
//subgroup的size为偶数。
(2)(\forall int i; 0 <= i && i < subgroup.length / 2; subgroup[i * 2].isLinked(subgroup[i * 2 + 1]))
//两个两个来看(a[0]a[1],a[2]a[3]......),可以理解为这是图的边集的子集
(3)(\forall int i; 0 <= i && i < people.length; isCircle(id, people[i].getId()) <==>
(\exists int j; 0 <= j && j < subgroup.length; subgroup[j].equals(people[i])))
//这里要求对于所有节点(person[i],都须满足如下条件:
//(由于是双箭头,可以理解为两侧同真或同假,即每个节点都要满足如下条件中的一个)
//1.和id可达,并且边集subgroup里存在一个边和该节点连着
//2.和id不可达,且subgroup里的任意一条边不能连着这个节点
//对于(3),可以总结为该边集subgroups的所有边连着的节点都是和id可达的。
(4)(\forall int i; 0 <= i && i < people.length; isCircle(id, people[i].getId()) <==>
(\exists Person[] connection;
(\forall int j; 0 <= j && j < connection.length - 1;
(\exists int k; 0 <= k && k < subgroup.length / 2; subgroup[k * 2].equals(connection[j]) &&
subgroup[k * 2 + 1].equals(connection[j + 1])));
connection[0].equals(getPerson(id)) && connection[connection.length - 1].equals(people[i])))
/**
(4)有点长,还需要拆分一下,
(\forall int i; 0 <= i && i < people.length; isCircle(id, people[i].getId()) <==> 公式1 )
公式1:(\exists Person[] connection; 公式2 ;公式3)
公式2:(\forall int j; 0 <= j && j < connection.length - 1; 公式4 )
公式3:connection[0].equals(getPerson(id)) && connection[connection.length - 1].equals(people[i])
公式4:(\exists int k; 0 <= k && k < subgroup.length / 2; subgroup[k * 2].equals(connection[j]) &&
subgroup[k * 2 + 1].equals(connection[j + 1]))
根据公式2和公式4可知,对于这个Person数组connection,需要满足任意的成员,都能存在subgroup里的一条边,这条边连着 connection[j]和connection[j+1],换句话说,这个connection的相邻元素都是可达的,也就是说connection是一条路径,该路径的边都在subgroup里
根据公式3可知,该路径的起始节点是id,终止节点是people[i]
分析完公式2和公式3,可以得到公式1的意思就是,subgroup这个边集里,存在这么一些边,能够构成一条从id到people[i]的路径
现在回到整个(4),对于任意一个节点(people[i]),如果people[i]和id可达,那么subgroup就存在这样id到people[i]的路径,如果不可达就不存在这样一条路径了。
**/
最终我们得到了该方法的目的是获取该节点对应的连通分量的最小生成子树的边的权值之和。
至于算法,我采用了克鲁斯卡尔+并查集优化,最后复杂度大约是O(nlogn),参考代码在
依然将算法和代码进行解离,将kruskal作为Network的一个属性进行维护和调用。
UML类图如下:
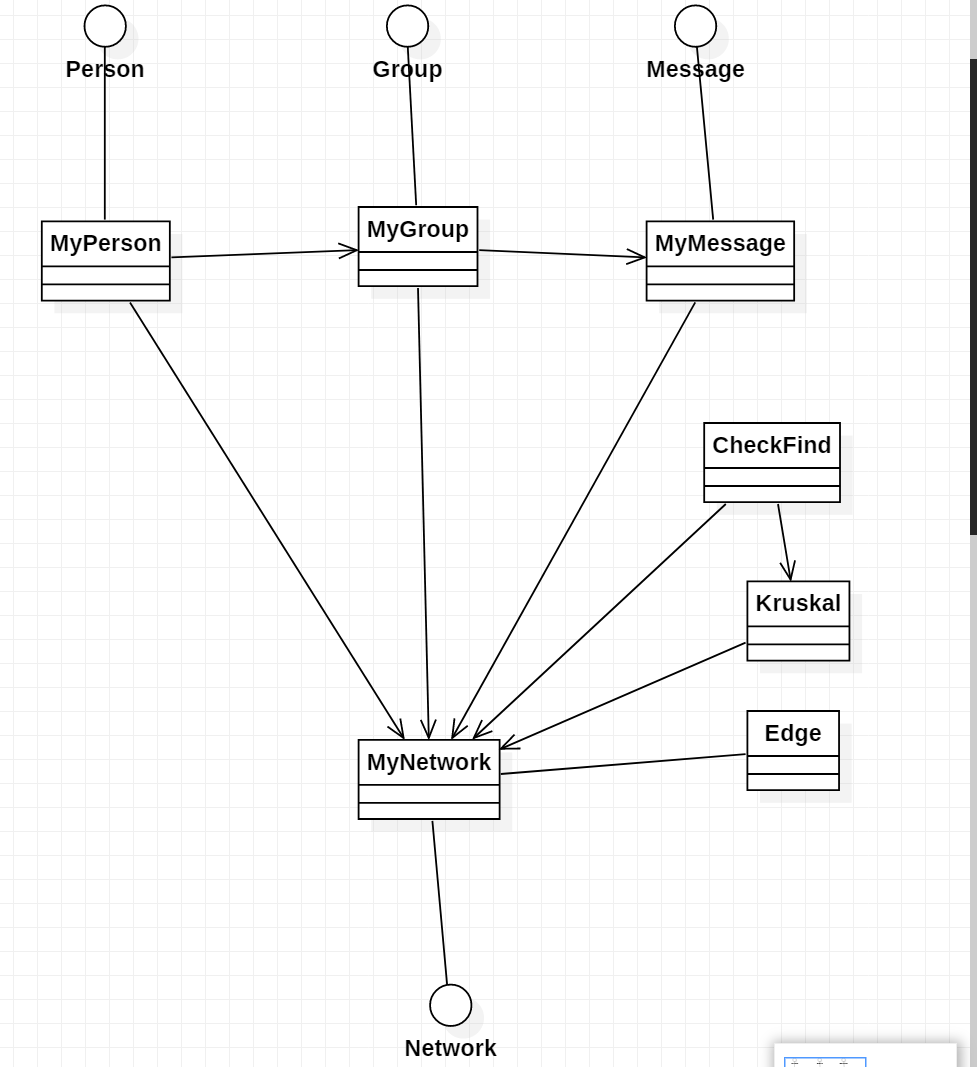
优化和维护策略
除了最小生成树算法,其他有几个方法还需要注意一下优化。其中queryGroupValueSum方法如果按照其JML规格来写的话,复杂度是O(n^2),当一个group里的person很多的时候,反复调用这个方法,时间将会巨慢,因此要想在互测时不被hack到,这个方法是一定要优化的。这个方法的意义就是求这个group里,所有person两两的queryValue之和,因此我稍微牺牲了atg和dfg方法的性能,让group里维护一个变量a,在一个group里加入(删除)person的时候,让a增加(减少)这个person和组内所有其他人的queryValue之和,并且对于ar指令,需要判断一下ar后的两个人是不是在一个group里,如果在的话需要让group里的a增加value。最后a*2即为结果。这样我将qgvs指令的复杂度降到了O(1),atg和dfg提高到了O(n),总体看性能是不错的。
其次,对于求group内people的年龄方差,也可以采用变量维护的方式,在加人和删人的时候始终维护people的age之和,和people的age的平方和,这样可以qgav指令优化到O(1)。
第11次作业
架构设计
本次作业多了很多种Message,包括红包、通知、表情,每种新型Message都有自己特殊的属性。因此在sendMessage的时候,其JML规格的复杂度也很高,需要考虑这种Message的情况,这里需要细心的阅读JML规格。本次作业需要新加的算法就是sendIndirectMessage方法,这个方法有一部分和sendMessage相似,特殊的地方就是需要我们求得Message中的两个节点的最短路径的权值和,这里我采用迪杰斯特拉算法,不过普通的迪杰斯特拉算法的复杂度是O(n^2),而是采用了堆优化的算法,利用java自带的PriorityQueue可以将求得最短边的时间复杂度从O(n)降到O(logn)。参考代码在
UML类图如下:
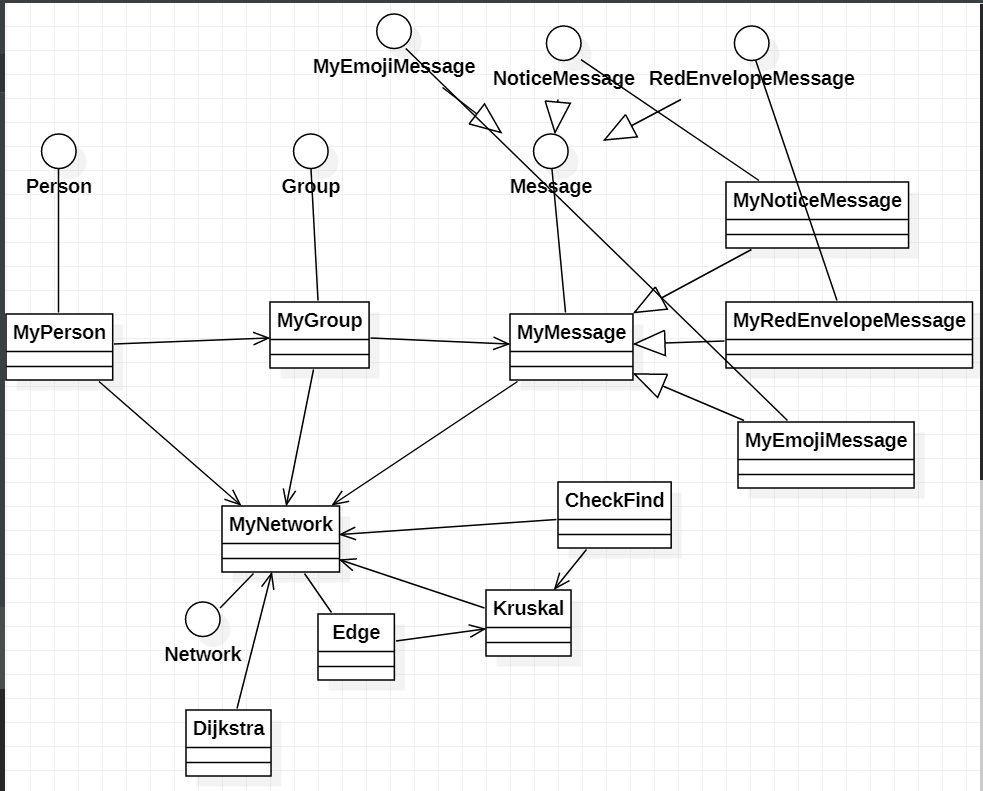
优化和维护策略
除了图算法和前两次作业的优化策略以外,本次作业似乎没有特别需要考虑优化维护的方法,不过需要注意的是能采用hashMap尽量采用hashMap,例如新加的emojiList和emojiHeatList,根据JML规格可以发现两个数组是一一对应的关系,因此采用hashMap即简化了复杂度,又方便阅读编写。
异常类的实现
三次作业的异常类其实没什么区别,利用static变量来存储该异常的出现次数和每个id对应的异常次数即可,只不过需要注意两个参数的时候需要进行排序,也要注意print方法的正确性。其实只要第一次作业写好了以后,后两次作业就基本一样了。
自测策略
本单元的自测策略主要就是,自动+手动构造测试数据、找同学对拍进行debug。我并没有采用JUnit来进行测试,也算是比较遗憾的地方。由于本次作业输出固定、输入格式固定,因此对拍也是颇为有效的方法。不过关键在于如何提高数据的强度,在自测的过程中我们会发现,其实纯随机数据是几乎没有什么强度的,因为纯随机数据会触发很多异常,导致最后相关指令很难被充分测试。因此手动构造对于我来说也很重要,手动构造的时候需要考虑如下几种情况:
-
在数据限制范围内,尽量保证人数够多,边数(关系)够多够复杂,组数够多并且每个组里有足够多的人,message的种类和数量足够多
-
在数据限制范围内,对于一些比较吃时间或者容易出错的指令(sm,qlc,qbs,sim,qgvs),尽量保证其数据量足够多。可以根据你想卡的指令来提高其指令的比例。
-
通过动态的改变整个社交网络从而能够充分测试,比如利用atg和dfg动态改变group,利用am、sm和sim来动态改变messages,利用dce、cn等动态改变特殊类型的message。
-
在动态改变整个社交网络的状态之后,尽量多用查询指令,例如qm、qp、qrm等等,这些会验证前面的一些指令的正确性,否则如果只用sm无法判断方法实现的正确与否
利用已经造好的数据集通过编写脚本与同学的代码进行对拍,输出不一样的地方可以直接找到对应的指令是什么,然后可以判断出大概是哪些指令可能有问题。通过这三次作业来看这种debug的效率还是很高的。
互测过程bug分析
互测过程跟自测过程差不多,将同房间的代码下载下来对拍。本单元的代码由于架构已经给出,所以大家的整体思路几乎差不多,这样如果发现bug可以直接肉眼定位到bug的位置和原因,从而进行hack。
互测过程中发现的bug:
-
第二次作业只要是qgvs的超时问题,或许是由于第一次作业就已经写好了qgvs,第二次作业就没有考虑其优化
-
第三次作业的bug种类比较多,bug的分布主要位于sm、dce指令,对于红包消息中money的改变出现错误、删除冷门表情时出现错误等等,不过第三次作业没有hack到超时的问题。
Network拓展
假设出现了几种不同的Person
-
Advertiser:持续向外发送产品广告
-
Producer:产品生产商,通过Advertiser来销售产品
-
Customer:消费者,会关注广告并选择和自己偏好匹配的产品来购买 -- 所谓购买,就是直接通过Advertiser给相应Producer发一个购买消息
-
Person:吃瓜群众,不发广告,不买东西,不卖东西
如此Network可以支持市场营销,并能查询某种商品的销售额和销售路径等 根据题目要求,我们可以推断Network还需要增加与市场营销相关的属性(advertise[],producers[],customers[],products[]等),而且需要添加和完善相关方法,比如说sm需要丰富一些对于购买消息的处理,增加挑选和偏好匹配产品的方法,发送产品广告等等。假设产品的属性不包括Advertiser,我们可以写出(完善)sendAdvertise,getProduct,sellProduct方法
/*@ public normal_behavior
@ requires containsProduct(id);
@ ensures (\exists int i; 0 <= i && i < products.length; products[i].getId() == id &&
@ \result == products[i]);
@ also
@ public normal_behavior
@ requires !containsProduct(id);
@ ensures \result == null;
@*/
public /*@ pure @*/ Product getProduct(int id);
/*@ public normal_behavior
@ requires !(\exists int i; 0 <= i && i < advertise.length; advertise[i].equals(advertise));
@ assignable people;
@ ensures advertise.length == \old(advertise.length) + 1;
@ ensures (\forall int i; 0 <= i && i < \old(advertise.length);
@ (\exists int j; 0 <= j && j <advertise.length; advertise[j] == (\old(advertise[i]))));
@ ensures (\exists int i; 0 <= i && i <advertise.length; advertise[i] == advertise);
@ also
@ public exceptional_behavior
@ signals (EqualAdvertiseIdException e) (\exists int i; 0 <= i && i < advertise.length;
@ advertise[i].equals(advertise));
@*/
public void sendAdvertise(/*@ non_null @*/Advertise advertise) throw EqualAdvertiseIdException
/*@ public normal_behavior
@ requires containsMessage(id);
/**省略了sm里的一部分
@ ensures (\forall int i; 0 <= i && i < \old(getMessage(id).getPerson2().getProducts().size());
@ \old(getMessage(id)).getPerson2().getProducts().get(i+1) == \old(getMessage(id).getPerson2().getProducts().get(i)));
@ ensures \old(getMessage(id)).getPerson2().getProducts().get(0).equals(\old(getMessage(id)));
@ ensures \old(getMessage(id)).getPerson2().getProducts().size() == \old(getMessage(id).getPerson2().getProducts().size()) + 1;*/
public void sellProduct(int id) throws ProductIdNotFoundException
学习体会
本单元收获很多:学习了如何阅读和理解JML规格、学习了如何利用JML规格的约束去实现代码、在写代码的过程中逐渐理解到了jml是如何将上层功能的设计与下层实现分离。也顺便复习了一下离散数学的知识。而且也学习了一些便于数据测试的方法。研讨课上在和同学们的讨论中也学习了如何分析和撰写JML规格。
当然也有反思的地方:没有采用JUnit进行方法的测试和验证,而且在实现方法的时候并没有按照面向对象的思想编写代码,更多的时候主要是面向过程的分析和实现。其次,有些JML规格并没有认真阅读,有的直接根据名字和向同学询问获得该方法的目的。实验课没有理解题目给出的JML规格的含义导致最后并没有做出来。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号