图总结

图的知识点总结

一、思维导图

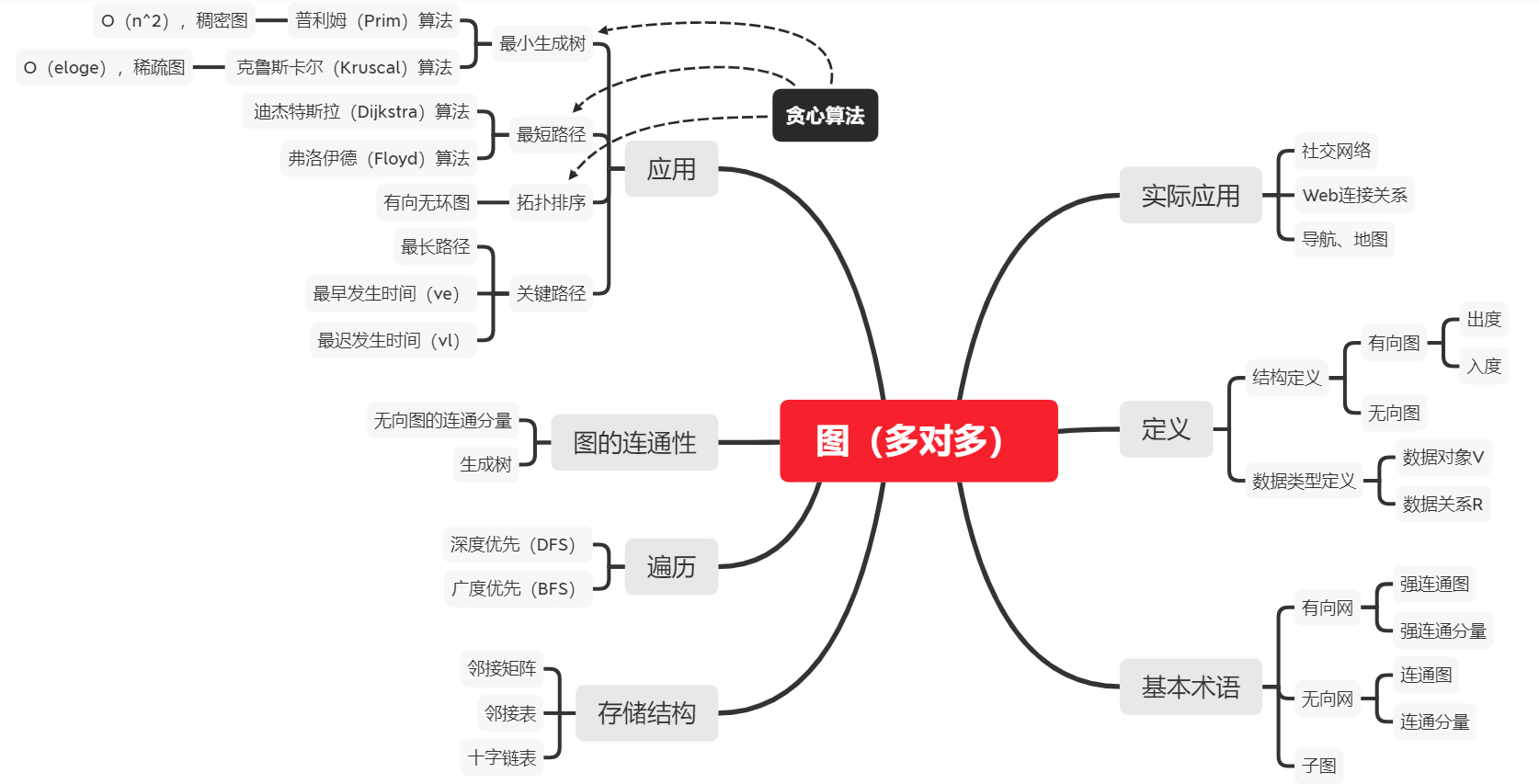
二、重要概念笔记

  1. 图的定义和基本术语

    1. 定义

      • 图：是由一个顶点集 V 和一个顶点间的关系集合 组成的数据结构。

      • “弧”是有方向的，因此称由顶点集和弧集构成的 图为有向图。

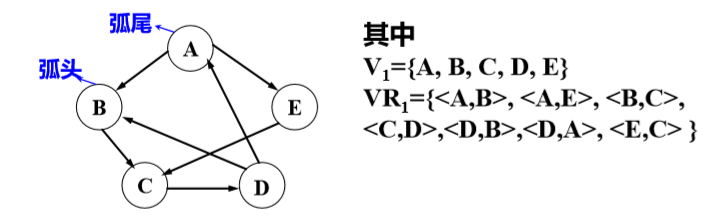
      • 由顶点集和边集构成的图称作无向图。

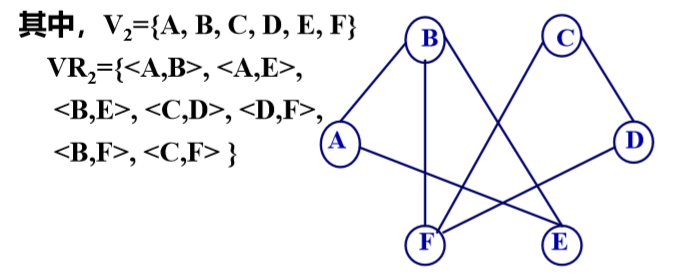
    2. 基本术语

      • 有（无）向网：弧或边带权的图

      • 完全图：含有e=n(n-1)/2条边的无向图

      • 有向完全图：含有e=n(n-1)条弧的有向图称作有向完全图

      • 稀疏图：e<nlogn；稠密图：e>=nlogn

      • 度=出度（以顶点v为弧尾的弧的数目）+入度（以顶点v为弧头的弧的数目）仅对有向图

      • 路径长度：从顶点v到顶点w路径上边的数目；简单路径：序列中顶点不重复出现的路径；简单回路：序列中第一个顶点和最后 一个顶点相同的路径

      • 对无向图：若图G中任意两个顶点之间都有路径相通，则称此图为连通图：若无向图为非连通图，则图中各个极大连通子图，称作此图的连通分量。对有向图：若任意两个顶点之间都存在一条有向路径，则称此 有向图为强连通图。否则，其各个强连通子图称作它的强连通分量。

  2. 图的存储结构

    1. 邻接矩阵： 无向图的邻接矩阵是对称的，有向图的邻接矩阵可能是不对称的。在有向图中：①出度：统计第i行1的个数②入度：统计第j列1的个数。

      含有n个顶点和e条边的无向图的邻接矩阵中，零元素的个数为：n^2-2e

      #define MaxInt 32767 //表示极大值 
#define MVNum 100    //最大顶点数 
typedef char VerTexType; 
//假设定点的数据类型为字符型 
typedef int ArcType; //假设边的权值类型为整型 typedef struct {     // 图的定义 
	VerTexType vexs[MVNum];     // 顶点表
    ArcType arcs[MVNum][MVNum]; 
    // 弧的信息(邻接矩阵) 
    int    vexnum, arcnum;      
    // 图当前的顶点数和边数 
 } AMGraph;  //邻接矩阵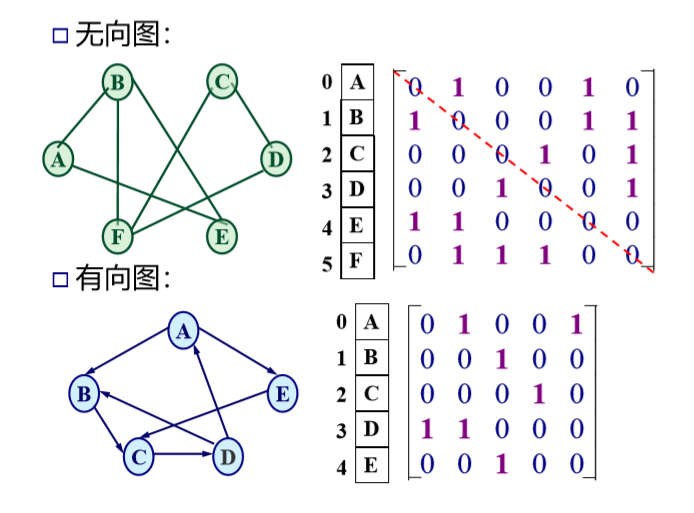

    2. 邻接表：邻接点域、链域、数据域。

      //表(弧/边)结点： 
typedef struct ArcNode {  
	int   adjvex; // 该弧所指向的顶点的位置 
	struct ArcNode *nextarc;//指向下一条弧的指针
	InfoType *info;  // 该弧相关信息的指针 
} ArcNode;
//头结点： 
typedef struct VNode { 
	VerTexType data;   // 顶点信息 
	ArcNode *firstarc; // 指向第一条依附该顶点的弧 
} VNode, AdjList[MAX_VERTEX_NUM];

      无向图邻接表：

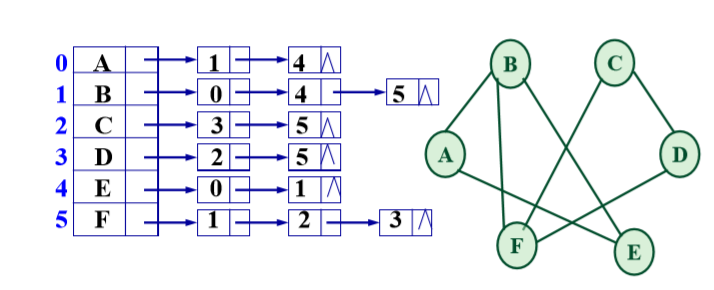
      有向图邻接表：

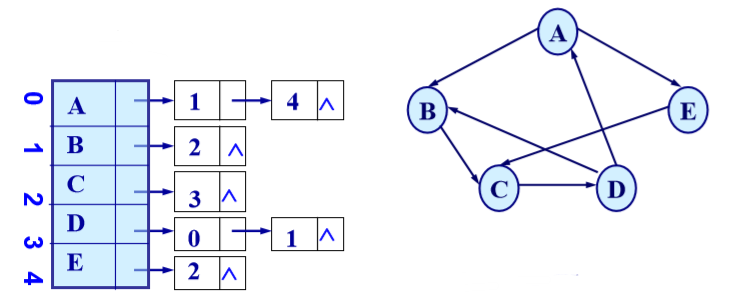
    3. 十字链表：从横向上看是邻接表，从纵向看是逆邻接表

      typedef struct ArcBox { // 弧的结构表示 
	int tailvex, headvex;   
	InfoType *info; 
	struct ArcBox *hlink, *tlink;   
} VexNode;
typedef struct VexNode { // 顶点的结构表示 
	VertexType  data; 
	ArcBox  *firstin, *firstout;   
} VexNode;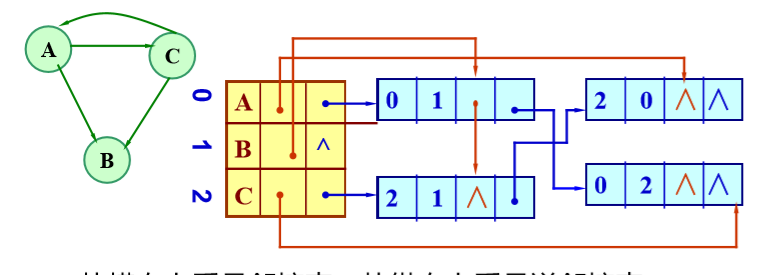

  3. 图的遍历

    1. 深度优先遍历（DFS）

      int visit[2*MAX];
void dfs(Graph G,int s){
      Arc* p = G.vex[s].firstArc;
      if(!visit[s]){
          printf("%4s",G.vex[s].data);
          visit[s] = 1;
      }
      while(p != NULL){
          if(!visit[p->adjvex])
              dfs(G,p->adjvex);
          p = p->nextArc;
      }
 }

    2. 广度优先算法（BFS）

      int q[2*MAX],f=0,r=0;
int visit_q[MAX];
  void bfs(Graph G,int s){
      if(!visit_q[s]){
          printf("%4s",G.vex[s].data);
          visit_q[s] = 1;
          Arc* p = G.vex[s].firstArc;
          while(p != NULL){
             if(!visit_q[p->adjvex])
                 q[r++] = p->adjvex;
             p = p->nextArc;
         }
     }
     while(f < r){
         bfs(G,q[f++]);
     }
 }

  4. 最小生成树

    构造的最小生成树并不一定唯一，但最小生成树的权值之和一定是相同的。

    1. 普利姆算法：

      #define INF 32767
void Prim(MGraph g,int v){
	int lowcost[MAXv];
	int min;
	int closest[MAXV],i,j,k;
	for(i=0;i<g.n;i++){
		lowcost[j]=g.edges[v][i];
		closest[i]=v;
	}
	for(i=1;i<g.n;i++){
		min=INF;
		for(j=0;j<g.n;j++){
			if(lowcost[j]!=0&&lowcost[j]<min){
				min=lowcost[j];
				k=j;
			}
			printf("边(%d,%d)权为：%d\n",closest[k],k,min);
			lowcost[k]=0;
		}
		for(j=0;j<g.n;j++){
		if(g.edges[k][j]!=0&&g.edges[k][j]<lowcost[j]){
				lowcost[j]=g.edges[k][j];
				closest[j]=k;
			}
		}
	}
}

    2. 克鲁斯卡尔算法：

      void Kruskal(MGraph g){
	int i,j,u1,v1,sn1,sn2,k;
	int vset[MAXV];
	Edge E[MaxSize];
	k=0;
	for(i=0;i<g.n;i++){
		for(j=0;j<g.n;j++){
			if(g.edges[i][j]!=0&&g.edges[i][j]!=INF){
				E[k].u=i;E[k].v=j;
				E[k].w=g.edges[i][j];
				k++;
			}
		}
	}
	InsertSort(E,g,e);
	for(i=0;i<g.n;i++) vest[i]=i;
	k=1;j=0;
	while(k<g.n){
		u1=E[j].u;v1=E[j].v;
		sn1=vset[u1];sn2=vset[v1];
		if(sn1!=sn2){
			cout<<u1,v1,E[j].w;
			k++;
			for(i=0;i<g.n;i++)
				if(vset[i]==sn2) 
					vset[i]=sn1;
		}
		j++;
	}
}

  5. 最短路径(与关键路径区分！)

    1. Dijkstra算法：把V分成两组： ⑴S：已求出最短路径的顶点的集合 ⑵T=V-S：尚未确定最短路径的顶点集合 将T中顶点按最短路径递增的次序加入到S中，保证：① 从源点V0到S中各顶点的最短路径长度都不大于从V0到T 中任何顶点的最短路径长度 ②每个顶点对应一个距离值： ③S中顶点：从V0到此顶点的最短路径长度 ④T中顶点：从V0到此顶点的只包括S中顶点作中间顶点的最 短路径长度

    2. Floyd算法：逐个顶点试探 从vi到vj的所有可能存在的路径中，选出一条长度最 短的路径。

  6. 拓扑排序

    按照有向图给出的次序关系，将图中顶点排成一个 线性序列，对于有向图中没有限定次序关系的顶点， 则可以人为加上任意的次序关系。 由此所得顶点的线性序列称之为拓扑有序序列(有向无环图)

    进行拓扑排序：①从有向图中选取一个没有前驱的顶点，并输出之； ②从有向图中删去此顶点以及所有以它 为尾 的弧； ③重复上述两步，直至图空，或者图不空但找不到无 前驱的顶点为止。

  7. 关键路径

    概念：

    事件vi的最早发生时间：从开始点v1到vi的最长路 径长度。用ve(i)表示。

    事件vi的最迟发生时间：在不推迟整个工期的前提 下，事件vi允许的最晚发生时间。用vl(i)表示。

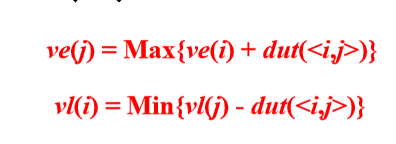
    关键路径(最长路径)：

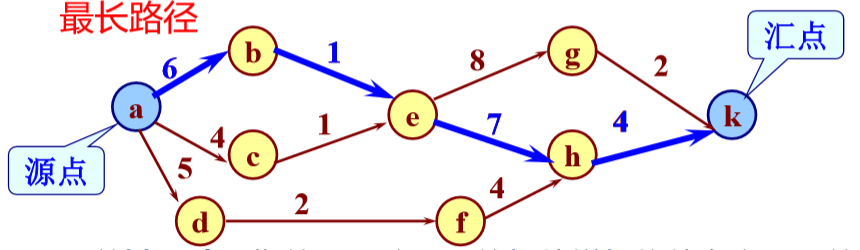
三、疑难问题及解决方案

1.pta 7-6 旅游规划

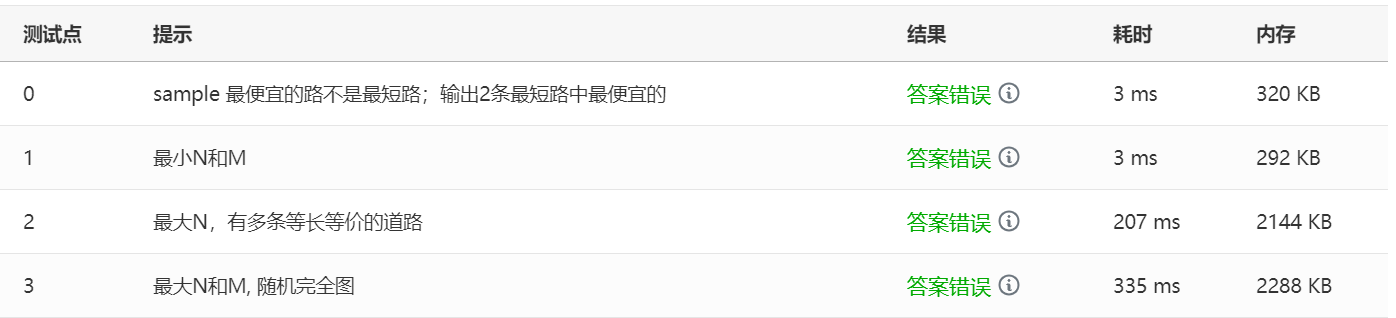
#include <stdio.h>
#include <stdlib.h>
#define T 500
#define INF 999999
int main(){
    int G[T][T];//存储最短距离 
    int p[T][T];//储存收费额
    int N,M,S,D;
    scanf("%d %d %d %d",&N,&M,&S,&D);
    //N城市个数 M高速公路条数 S出发地编号 D目的城市编号 
    for(int i=0;i<N;++i){
        for(int j=0;j<N;j++){
            G[i][j]=INF;
            p[i][j]=INF;
        }
    }
    //初始化最短距离和收费额二维数组，当然用一个三维数组p[N][N][2]也是可以的 
    int c1,c2,ml,pay;
    for(int i=0;i<M;i++){
        scanf("%d %d %d %d",&c1,&c2,&ml,&pay);
        G[c1][c2]=G[c2][c1]=ml;//输入两个城市之间的高速公路距离 
        p[c1][c2]=p[c2][c1]=pay;//输入两个城市高速公路的收费额 
    }
    for(int k=0;k<N;k++){//用Floyd算法计算最短距离 
        for(int i=0;i<N;i++){
            for(int j=0;j<N;j++){
                if(i!=j&&j!=k){
                    if((G[i][k]+G[k][j])<G[i][j]){
                        G[i][j]=G[i][k]+G[k][j];
                        p[i][j]=p[i][k]+p[k][j];//上述第一种情况 
                    }
                    else if(((G[i][k]+G[k][j])==G[i][j])&&((p[i][k]+p[k][j])<p[i][j])){
                        p[i][j]=p[i][k]+p[k][j];
                    }
                }
            }
        }
    }
    printf("%d",G[S][D],p[S][D]); 
}
2.其他问题：

对于图的知识点，算法较多，很容易混杂 ，就上述的算法中刚开始可以分辨清楚，多了起来之后，就会混杂在一起。可能是自我概念还比较模糊，会继续加强概念的巩固。

posted @ 2020-05-17 15:40  羊腿桂鱼yu  阅读(315)  评论(0)  编辑  收藏  举报